基于概率协作表示的几何保持图嵌入

刘 勇，杨园园，苟建平，刘志锋

(1.四川轻化工大学 人工智能四川省重点实验室，四川 自贡 643002；2.江苏大学 计算机科学与通信工程学院，江苏 镇江 212013)

近年来，快速发展的智能传感信息技术产生了大量视觉图像数据.由于这些图像通常分布在高维空间，其内在结构特征在信息处理与分析过程中难以发掘，其算法学习过程中容易形成“维度灾难”，因此有必要对图像进行降维处理.在机器学习领域中，绝大多数降维方法是线性的，且大都可以统一到图嵌入框架中[1].

在线性降维技术中，主成分分析(principle correlation analysis，PCA)、线性可鉴别分析(linear discriminant analysis，LDA)和局部保持投影(locality preserving projections，LPP)[2]是图嵌入框架下的3种经典方法.PCA主要通过最大化协方差矩阵来寻找最优投影矩阵，是一种无监督方法.LDA是一种有监督方法，通过最大化类间离散度与最小化类内离散度来学习最优投影矩阵.PCA没有利用标签信息，不能较好用于分类，而LDA考虑标签信息却导致小样本问题.PCA和LDA仅强调数据的全局结构而忽视了数据的局部结构.为了利用数据的局部结构信息，局部保持投影(LPP)是一种典型的保持高维数据局部流形结构特征的线性方法.基于LPP的思想和优点，近年来提出很多基于LPP的扩展新方法[3-5].文献[3]提出了快速正交保局投影(fast and orthogonal locality preserving projections，FOLPP)，在正交约束下，最大化全局最小化局部，快速学习正交投影矩阵.文献[4]提出了保持局部相似性的可鉴别(local similarity preserving discriminant，LSPD)投影降维方法，且其扩展方法(LSPD+)在保持样本局部相似性的同时，还保持数据的几何结构信息.文献[5]提出了稳定正交局部判别嵌入(stable orthogonal local discriminant embedding using trace ra-tio，SOLDE-TR)，构造数据结构的3个邻接图，并使用迹比准则求解最优投影矩阵.

线性表示学习在模式分类中取得了显著的分类效果.在降维技术中，利用数据表示隐含潜在的数据几何和判别信息，提出了一些基于表示学习的图嵌入新方法.文献[6]采用稀疏表示自动构图，稀疏系数作为图的边权重，提出稀疏保持投影(sparsity preserving projections，SPP)的降维方法.鉴于SPP良好的降维效果，文献[7]提出稀疏与几何保持图嵌入(sparsity and geometry preserving graph embedding，SGPGE)方法，其使用稀疏表示重构样本，并设计反映数据几何分布和判别信息的构图方式.文献[8]提出基于协作表示的投影(collaborative representation based projections，CRP)的方法，其采用协作表示构图，协作表示系数作为图的边权重.鉴于CRP是一种无监督的方法，文献[9]提出的可鉴别协作表示图嵌入(collaborative representation discri-minant embedding，CRDE)，在表示构图中充分利用类别标签信息.

尽管数据表示重构样本可以在一定程度上捕获数据的一些本质特征，但是样本的可鉴别信息和几何分布信息没有被充分考虑，导致高维数据在子空间中分类效果不好.为了提高高维数据在低维空间中的表示和识别能力，文中提出一种基于概率协作表示的几何保持图嵌入(probabilistic collaborative representation geometry preserving graph embedding，PCRGPGE)方法.PCRGPGE采用概率协作表示重构样本[10]来充分捕获数据的本质特征信息，并采用考虑内类和类间样本点的几何分布的可鉴别构图方式.通过将所提PCRGPGE与相关的经典和新的图嵌入方法在高维人脸数据集上进行对比试验.

1 相关投影方法

首先设X=[X1,X2,…,XC]=[x1,x2,…,xn]∈Rd×n表示一个高维数据集，Y=[y1,y2,…,yn]∈Rr×n表示X从原始高维空间投影到低维子空间所对应的集合，Xi是第i类的样本集.其中，d和r分别是原始高维空间和低维子空间的特征维度，n是样本总个数，每个样本xi对应的类标签是ci∈{1,2,…,C}，C是类别个数.

1.1 局部保持投影(LPP)

局部保持投影方法[2]是一种典型的基于流形学习的图嵌入降维方法，其采用近邻构图方式构造高维数据邻接图来反映原始高维数据的局部流形结构.LPP使得原始高维空间中的相似样本在低维子空间中也保持相似.在近邻构图的邻接矩阵W中，样本xi与xj之间权重的wij计算式为

(1)

式中：N(xj)为样本xj的k个近邻集合；t为正的可调整因子.基于近邻构图方式，LPP目标函数定义如下：

(2)

式中：p为投影矩阵P的任意一个投影向量.式(2)经过简单计算转化成一般特征值求解问题，如下：

XLXTp=λXDXTp,

(3)

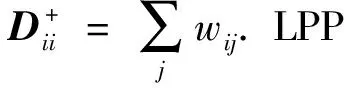
1.2 基于协作表示的投影(CRP)

基于协作表示的投影[9]采用协作表示自动构图来反映数据的结构特征，其协作表示系数作为图的边权重.协作表示构图模型如下：

(4)

式中：wi=[wi1,wi2,…,wii,…,win]T∈Rn，其中wii=0表明去除X中的样本xi，即xi在数据表示中不参与表达自身，wij(i≠j)表示每一个xj对于重构xi的贡献，在协作表示构图中定义为xj到xi的边权重；λ为调整因子.

利用协作表示构图，定义局部紧致离散度如下：

(5)

式中：SL=X(I-W-WT+WWT)XT是局部离散矩阵，且W=[w1,w2,…,wn]T为协作表示构图的邻接矩阵.同时，定义全局分离离散度如下：

(6)

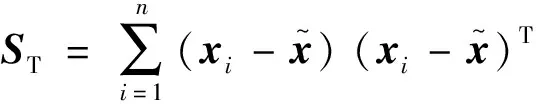
CRP的目标函数定义如下：

(7)

经过简单计算，式(7)转化成如下一般特征值求解问题：

STP=λSLP.

(8)

CRP的最优投影矩阵P由式(8)的前r个最大特征值对应的特征向量组成.

2 基于概率协作表示的几何保持图嵌入

2.1 基本思想

为了充分获取高维数据的结构信息并保持在子空间中，增强数据的模式判别能力，基于概率协作表示的几何保持图嵌入(PCRGPGE)利用概率协作表示重构高维数据样本，获取数据的自然判别信息和数据结构信息.而且，PCRGPGE采用一种新的可鉴别构图方式，考虑类内和类间数据点的几何分布信息，构建类内和类间的邻接图，进一步增强类内的紧致和类间的分离度.在PCRGPGE中，假定相似的高维样本所对应的概率协作表示重构样本也相似，其重构样本在低维空间中也保持相似，反之亦然，从而建立图嵌入目标函数，求解高维数据向低维子空间转化的投影矩阵，增强高维数据在低维子空间中的表示和判别能力.PCRGPGE的基本思想框架如图1所示.

图1 PCRGPGE基本思想框架

2.2 概率协作表示构图

根据概率协作表示的原理[10]，xi的概率协作表示模型定义如下：

(9)

式中：si=[si1,si2,…,sii,…,sin]T∈Rn，其中sii=0表明从X去除样本xi，sij(i≠j)表示每一个样本xj对于重构样本xi的贡献大小；ga和ka为调整因子.通过求解式(9)，得到

(10)

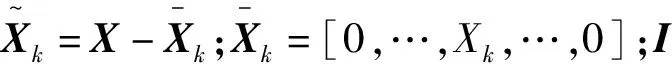
2.3 类内与类间构图

为了充分反映高维数据的几何结构信息和判别信息，PCRGPGE采用文献[11]的类内和类间构图方式.

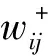
(11)

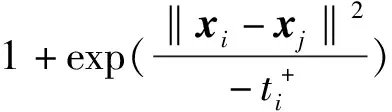
(12)

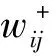
(13)

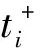
(14)

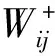
(15)

(16)

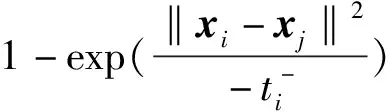
(17)

(18)

(19)

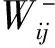
(20)

2.4 类内与类间几何保持离散度

在PCRGPGE中，假定原始空间中类别相同的2个样本xi与xj相似，则其概率协作表示重构Xsi与Xsj也相似，其重构样本在低维子空间中也应该保持相似.根据假定，为了保持类内样本的相似性和增强紧致度，定义图嵌入子空间中的类内几何保持离散度为

(21)

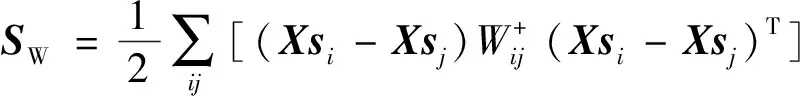
Xsj)T]=XSL+STXT，

(22)

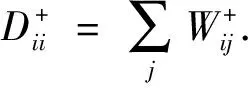
同样在PCRGPGE中，也假定原始空间中类别不同的2个样本xi与xj不相似，则其概率协作表示重构Xsi与Xsj也不相似，其重构样本在低维子空间中也应该保持不相似.根据该假定，为了保持类间样本的几何信息和增强区别，定义图嵌入子空间中的类间几何保持离散度为

(23)

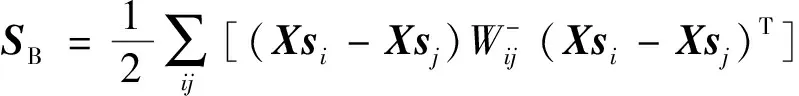
是类间几何保持离散度矩阵，且经过简单运算可以转化为

Xsj)T]=XSL-STXT，

(24)

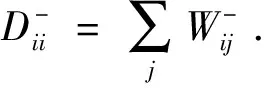
2.5 目标函数

PCRGPGE采用最大化类间几何保持离散度JB(p)和最小化类内几何保持离散度JW(p)，并在投影向量正交约束下，其目标函数定义如下：

(25)

式(25)经过拉格朗日乘数法，转化为如下一般特征值求解问题：

XS(L--L+)STXTp=λp.

(26)

通过计算式(26)最大特征问题，最优投影矩阵P由前r个最大特征值所对应的特征向量组成，即：P=[p1,p2,…,pr].综上，PCRGPGE方法的输入：使用PCA对输入训练样本X预处理；其输出：最优投影矩阵P.方法流程如下：① 根据式(10)计算概率协作表重构X的表示系数矩阵S；② 构造类内与类间邻接图，根据式(15)和(20)计算权重矩阵W+和W-；③ 根据式(22)和(24)计算基于概率协作表示的类内与类间拉普拉斯矩阵L+、SW和L-、SB；④ 根据式(26)，计算投影转化矩阵.

3 试 验

为了验证PCRGPGE的有效性，在2个经典的人脸图像数据集上，将其与PCA、LDA、LPP、FOLPP、SPP、CRP、CRDE、LSPD+、SOLDE-TR和SGPGE进行对比试验.在所有对比方法所学习的低维子空间中，采用简单的近邻方法作为分类器，测试高维数据在低维空间的识别能力.

3.1 数据集

将本方法分别在PIE29和IMM数据集上进行验证.人脸数据集PIE29共有1 632张图片，68个类别，每类有24张图片；人脸数据集IMM包含240张图片，共40类，每类有6张图片.在试验中，每张图片都采样成32×32的像素大小并拉伸成2 014维，并灰度量纲一化到0～1区间.分别来自PIE29和IMM数据集上某一类图像样本示例如图2所示.

图2 2个数据集的样本示例

3.2 参数选择

在PCRGPGE方法中，涉及到式(10)中概率协作表示重构的2个参数ka和ga和类间与类内构图的参数q.为了使得高维数据在低维空间的表达和识别能力达到最佳效果，试验中q的取值范围是1.0到3.0，步长是0.5；ka与ga的取值范围是0.1到1.0，步长是0.1.在试验中，随机选取每类中的l个样本作为训练样本，剩余作为测试样本.每个数据集随机这样划分30次，这30次试验的平均值作为最后的试验结果.PIE29每类训练样本l选取为8，IMM每类训练样本l选取为2.

根据文献[7]、[11]研究结果和文中的试验可知，所提出方法所采取的构图方式，其参数q取值1.5时，低维空间的识别效果最好.在此，当q=1.5时，给出所提出方法的识别精度随参数ka和ga变化的试验结果，如图3所示.

图3 PCRGPGE的识别率随参数的变化

由图3可见，参数ka对分类结果的影响相对比较小，而参数ga的影响很大.试验结果表明，概率协作表示重构样本能明显提高图嵌入子空间的模式判别能力.因此，在后续试验中，在数据集上的参数设置如下：在PIE29集上q=1.5，ka=0.1，ga=0.4；在IMM数据集上q=1.5，ka=0.5，ga=1.0.

3.3 试验结果

采用3.2节的参数设置，将PCRGPGE与其他图嵌入方法进行对比.试验主要对比各方法的识别结果随子空间维度的变化和各方法在子空间中获得的最好识别结果.

首先给出各对比方法在2个人脸数据集上的识别结果随维度变化的结果，如图4所示.需要强调的是，图4只列出了子空间维度在1～45的变化，且能说明各对比方法的变化趋势.由图4可见，各方法的识别率在维度空间较小时迅速提高，随着维度的增大，各方法的识别精度增长缓慢或者保持稳定.而且，图4试验结果验证PCRGPGE方法较其他对比方法，在维度变化过程中都取得较好的分类结果.

根据图4各方法的识别结果随维度变化，给出各方法在子空间维度变化中取得的最好识别结果及其偏差，如表1所示.

图4 各对比方法的识别率随维度的变化

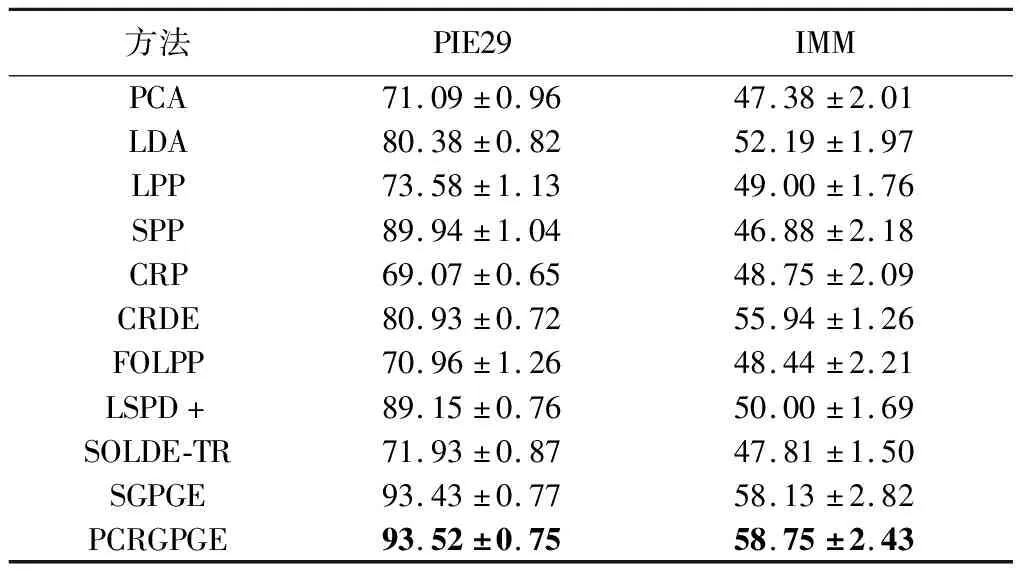
表1 各对比方法的识别率及其偏差 %

由表1可见，在所有对比方法中，PCRGPGE方法取得了最好的识别结果.通过以上结果分析可见，PCRGPGE方法在低维子空间中具有较好模式表达和判别能力，可以较好地保持高维数据的结构特征和判别信息，是一种较好的图嵌入降维技术.

4 结 论

文中提出基于概率协作表示的几何保持图嵌入降维新方法，通过概率协作表示重构和类内与类间的构图方式，将高维数据的几何结构和判别信息保持在低维子空间中.通过在人脸数据集上与相关图嵌入方法进行对比试验，结果表明所提出方法增强了高维数据在低维子空间中的有效特征表达和模式判别能力，是一种有效的图嵌入降维方法.在此后的研究工作中，将进一步研究协作表示与图嵌入的同步学习过程.