模糊有界完备domain及其基本性质
马娜娜, 罗清君
(西安财经大学 统计学院,陕西 西安710100)
Domain理论产生于20世纪60年代末70年代初,其目的是为Strachey的指称语义学提供模型,是理论计算机科学的数学基础之一.序和拓扑的相互结合、相互作用是这一理论的基本特征.1980年,Gierz等[1]对连续格的内容和思想进行了系统的研究.2003年,Gierz等[2]重新修订了专著[1],对连续格和Domain理论的发展做了阶段性总结.2013年,Goubault-Larrecq[3]介绍了Domain理论与非T2拓扑的紧密联系.经过40多年的发展,Domain理论已有丰富的成果和广泛的应用,并与拓扑学和范畴论等众多数学分支有着紧密的联系[4-6].
模糊Domain理论是把模糊集理论应用到Domain理论中,其最大的优点在于强调与模糊集理论的直接联系,从而可以运用模糊集理论作为工具,使许多问题得以顺利解决.目前,模糊Domain理论及相关领域已经取得了较为丰富的研究成果[7-16],并与拓扑学、范畴论和理论计算机科学等众多学科发生了非常密切的联系,但关于模糊有界完备domain的性质还尚无涉及.基于此,本文引入模糊有界完备domain和模糊Scott domain的概念,研究它们的模糊闭包算子的像以及模糊保序映射等一些基本的性质.证明在相应条件下,IL(X)是模糊Scott domain,并在此基础上给出模糊有界完备domain的等价刻画.
1 预备知识
下面给出完备剩余格和模糊偏序集中的一些基本概念和结论.
定义1.1[17]作为一个泛代数,一个剩余格是一个(2,2,2,2,0,0)型代数(L;∧,∨,*,→,0,1)(有时简记为(L,*)或仅为L)满足:
(RL1)(L;∧,∨,0,1)是有界格,0、1分别为最小元和最大元;
(RL2)(L;*,1)是交换幺半群,且*双侧保序;
(RL3)∀x,y,z∈L,x*y≤z当且仅当

若L是完备格,则称L是完备剩余格.
定理1.2[18]设L是剩余格,则成立:
(R1)a*b≤a∧b;
(R2)a=1→a;
(R3)a≤b⇔a→b=1;
(R4)a→(b→c)=(a*b)→c;
(R5)a→b≥b;
当L是完备格时,则成立:
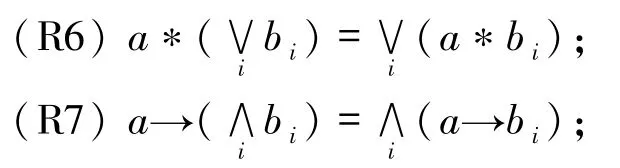
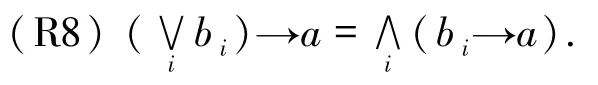
文中若无特别说明,L均表示一个完备剩余格.
定义1.3[7,14]设X是一个集合,e:X×X→L是一个映射.若满足:∀x,y,z∈X,成立:
(E1)e(x,x)=1(自反性);
(E2)e(x,y)*e(y,z)≤e(x,z)(传递性);
(E3)e(x,y)=e(y,z)=1⇒x=y(反对称性);则称(X,e)是模糊偏序集,e称为X上的模糊偏序.有时也把(X,e)简记为X.
定义1.4[7,14]设(X,e)是模糊偏序集,x0∈X,∀A∈LX.若满足:
1)∀x∈X,A(x)≤e(x,x0)(相应地,A(x)≤e(x0,x));
在定义1.4中,如果x0和A满足条件1),此时称x0为A的上界(相应地,下界).
定理1.5[7]设(X,e)是模糊偏序集,A∈LX,则

定义1.6[7]设(X,e)是模糊偏序集,若∀A∈存在,则称模糊偏序集(X,e)模糊完备格.
设f是模糊偏序集(X,eX)和(Y,eY)之间的映射.若

则称f是模糊保序映射.若f是双射且f,f-1是模糊保序映射,则称f是模糊序同构.
定义1.7设f:X→Y是一个映射.Zadeh前置幂集算子

和Zadeh后置幂集算子
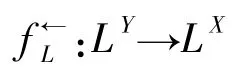
分别定义为:
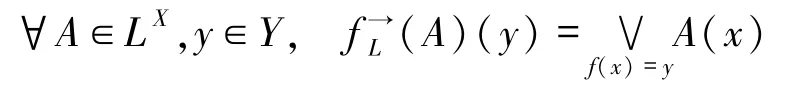
和
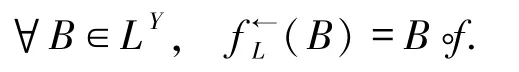
定义1.8[19]设(X,e)是模糊偏序集,D∈L X,,且
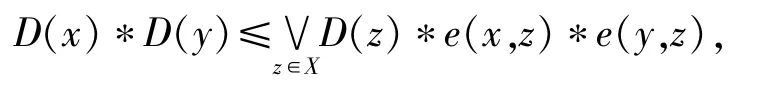
则称D为一个模糊定向子集.若模糊定向子集I∈L X是模糊下集,则称I为一个模糊理想.模糊偏序集(X,e)的全体模糊定向子集(模糊理想)的全体记为DL(X)(IL(X)).
定义1.9[20-21]设(X,e)是模糊Dcpo,∀x∈X,定义⇓x∈L X为

定义1.10[20-21]设(X,e)是模糊Dcpo,x∈X.定义映射k x:X→L为∀y∈X,则
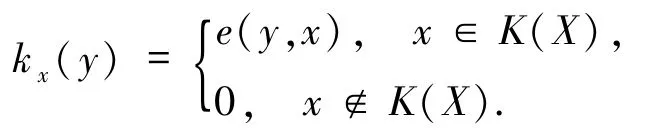
若k x是X的模糊定向子集且则称X是代数模糊domain.
定义1.11[22]设(X,e)是模糊偏序集,f:X→Y为映射,若f满足

且
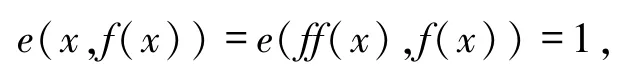
则称f为X上的一个模糊闭包算子.
2 模糊有界完备domain
下面引入模糊有界完备domain的概念,主要研究其上的模糊闭包算子的像以及模糊保序映射等一些基本的性质.
定义2.1[23]设(X,e)是模糊偏序集,如果∀A∈L X,当A有上界时存在,则称(X,e)为模糊有界完备的.
定义2.2设(X,e)是模糊domain,如果(X,e)为模糊有界完备的,则称(X,e)是模糊有界完备domain.
定理2.3设(X,e)是模糊有界完备domain,若c:X→X是保模糊定向并的模糊闭包算子,则c(X)是模糊有界完备domain,且
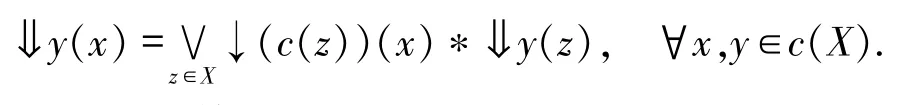
证明第一步,c(X)是模糊Dcpo.
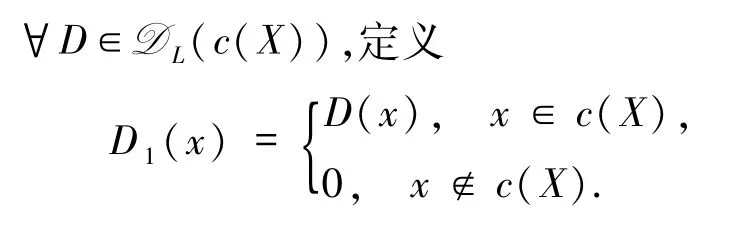
由于(X,e)是模糊有界完备domain,有
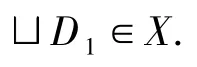
下证
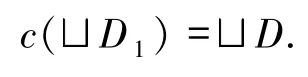
对任意x∈c(X),则
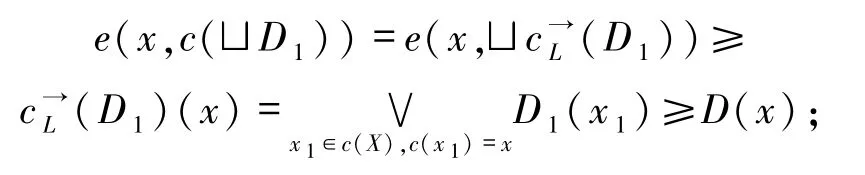
反之,对任意y∈c(X),则

综上
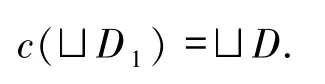
第二步,c(X)是模糊domain.设y∈c(X),x∈X,I∈IL(c(X)),则
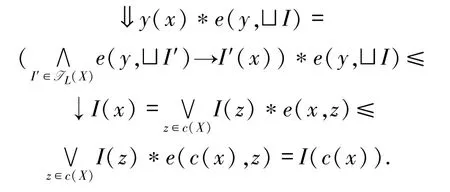
因此

下证∀y∈c(X),⇓y∈IL(c(X)).由于
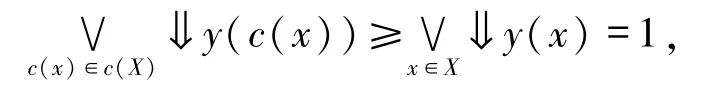
对任意x,x2∈c(X),则
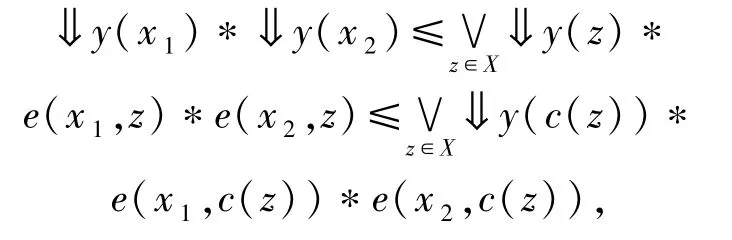
容易证明⇓y是c(X)中的模糊下集.
综上,⇓y∈IL(c(X)).
由于(X,e)是模糊有界完备domain,有
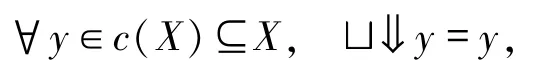
又c:X→X保模糊定向并,则
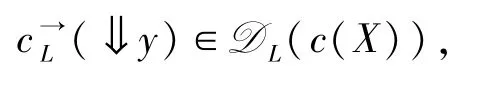
且
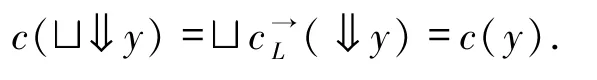
下证c(X)是模糊连续的.

反之,显然成立.
综上,c(X)是模糊domain.
第三步,c(X)是模糊有界完备的.∀A∈Lc(X),x0为A的上界,即
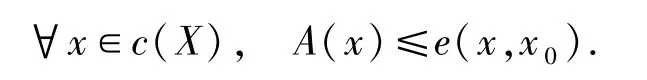
定义
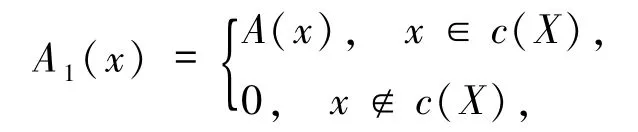
则A1∈LX,且A1的模糊上界为x0,根据X是模糊有界完备的,得到存在.

因此

最后,证明对任意x,y∈c(X),则
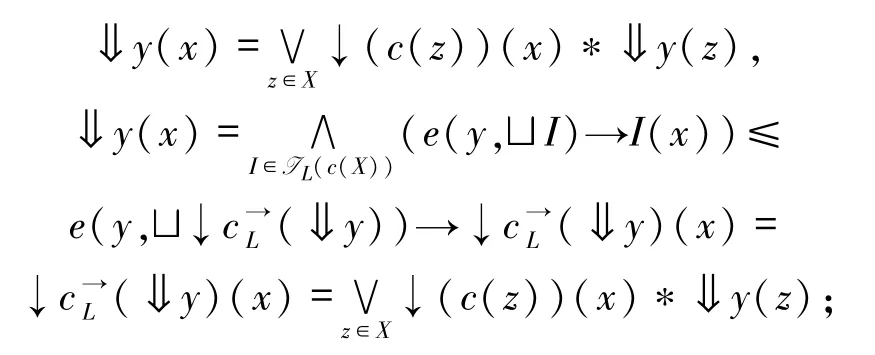
反之
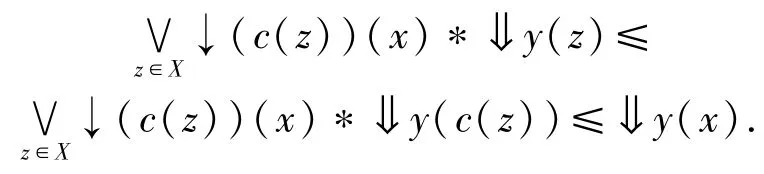
推论2.4设(X,e)是模糊有界完备domain,若c:X→X是保模糊定向并的模糊闭包算子,则
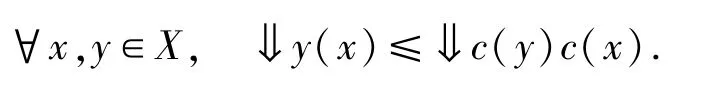
证明∀x,y∈X,⇓y(x)≤⇓y(c(x))=
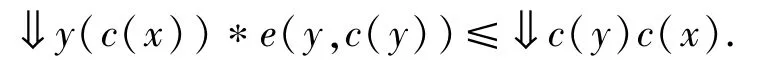
定理2.5设(X,e)是模糊有界完备domain,(Y,e)是模糊连续格,用(X→Y)表示所有的模糊保序映射,∀f∈(X→Y),定义k(f):X→Y为
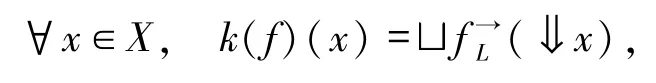
有:
1)k(f)∈(X→Y);
2)若用[X→Y]表示

则f保模糊定向并.
证明1)∀x1,x2∈X,则
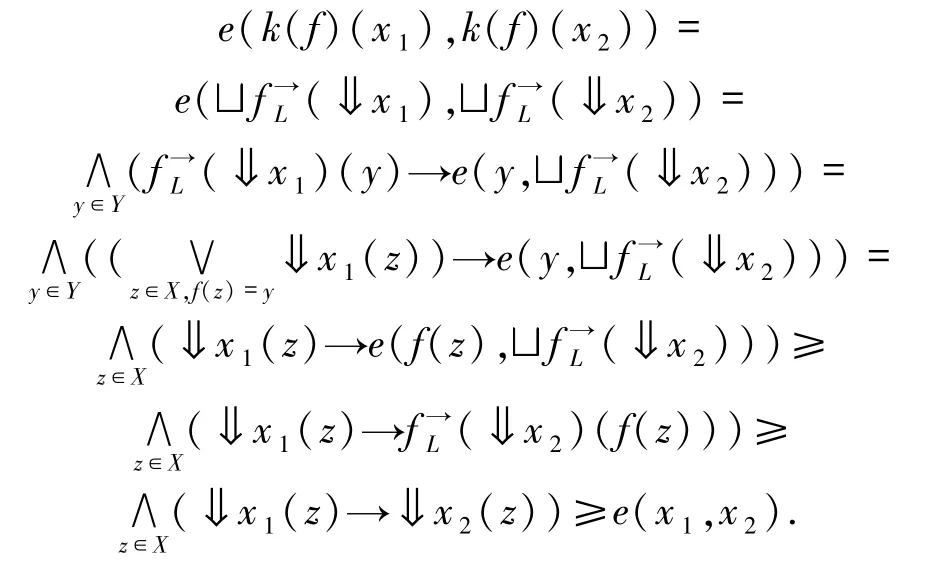
因此,k(f)∈(X→Y).
一方面
另一方面
综上,f保模糊定向并.
3 模糊Scott domain
下面研究模糊Scott domain中模糊闭包算子的像的性质,证明在相应条件下,IL(X)是模糊Scott domain,在此基础上给出模糊有界完备domain的等价刻画.
定义3.1[20-21]设(X,e)是模糊Dcpo,x∈X.如果⇓x(x)=1,则称x是X中的L-紧元.X中L-紧元的全体记为K(X).
定义3.2设(X,e)是模糊有界完备的Dcpo,x∈X.定义映射k x:X→L为∀y∈X,则
若k x是X的模糊定向子集且则称X是代数模糊有界完备domain,也称为模糊Scott domain.
命题3.3设(X,e)是模糊Scott domain,则(X,e)是模糊有界完备domain.
命题3.4设(X,e)是模糊Scott domain,c:X→X是保模糊定向并的模糊闭包算子,有:
1)c(X)是模糊Scott domain;
2)若L是frame且1◁1,则
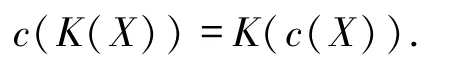
证明1)由定理2.3,c(X)是模糊有界完备domain.仅需证明c(X)是代数的.∀c(x)∈c(X),由于(X,e)是模糊Scott domain且c:X→X是保模糊定向并的模糊闭包算子,则k x是X的模糊定向子集且又根据推论2.4知c(K(X))⊆K(c(X)).
下证
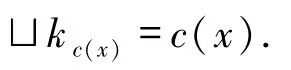
一方面

另一方面
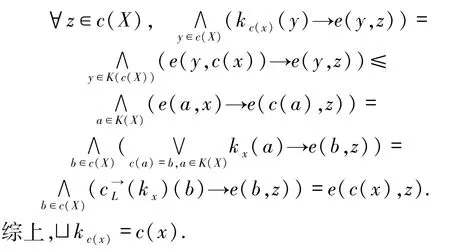
2)由1)知c(K(X))⊆K(c(X)).
下证
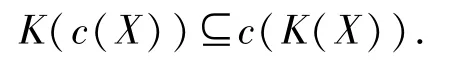
根据定理2.3,∀x∈K(c(X)),则
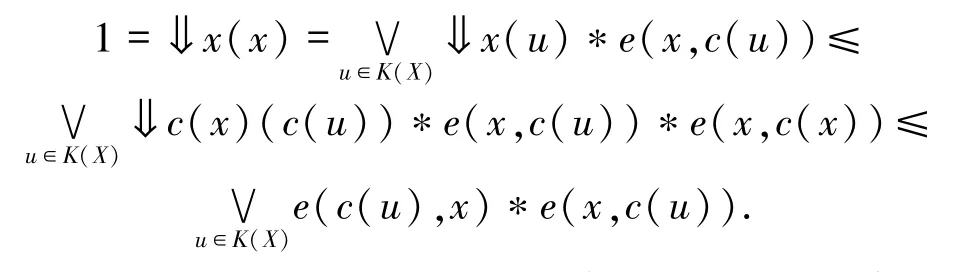
由于L是frame且1◁1.因此,存在u∈K(X),使得x=c(u),从而
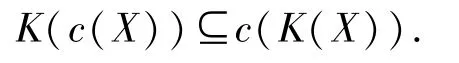
引理3.5设(X,e)是模糊偏序集,∀A∈LX,存在x0∈X使得A(x0)=1,则(X,e)是模糊有界完备的当且仅当存在.
证明必要性 设∀A∈LX,A有上界,即∀x∈X,存在y∈X使得A(x)≤e(x,y),则

因此,Au≠0L.根据存在,这说明(X,e)是模糊有界完备的.
充分性 设∀0L≠A∈LX,根据题意知存在x0∈X使得A(x0)=1,由于
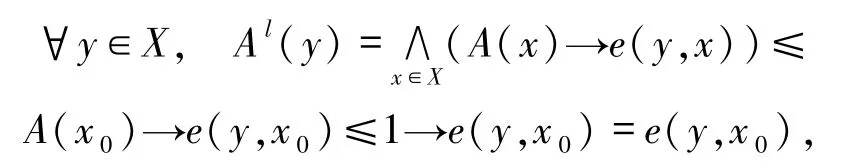
这说明Al有上界.因此知存在.
引理3.6设(X,e)是模糊有界完备domain,L=[0,1],∀Φ∈LIL(X),存在I0∈X使得 Φ(I0)=1,则IL(X)是模糊Scott domain.
证明文献[20-21]已经证明当(X,e)是模糊domain时,IL(X)是代数模糊domain,在这里只需证明当(X,e)是模糊有界完备时,IL(X)是模糊有界完备的.设
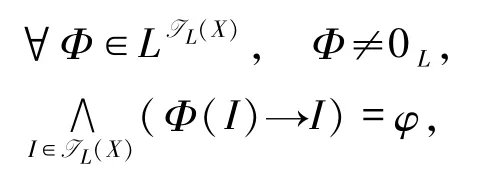
下证 φ∈IL(X).
1)φ是模糊下集.

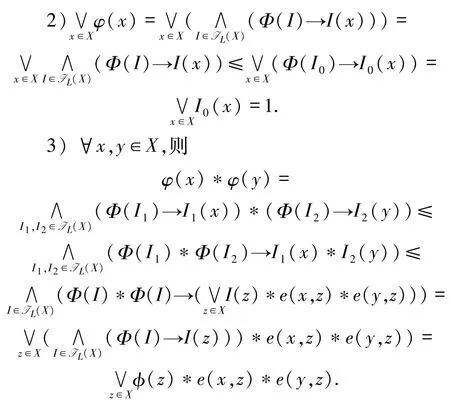
定理3.7设(X,e)是模糊Dcpo,则(X,e)是模糊有界完备domain当且仅当存在模糊Scott domain(Y,e),r:Y→X使得r是保模糊定向并的满射且r有左伴随.
证明必要性 令Y=IL(X),根据引理3.6可知IL(X)是模糊Scott domain.定义r:Y→X为
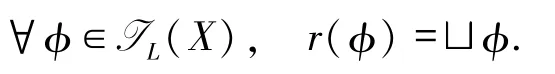
容易验证r是满射且有左伴随.根据文献[20-21],易证
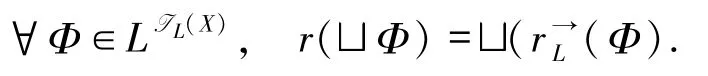
因此,r保模糊定向并.
充分性 设h是r的左伴随,则h保模糊定向并.由于r:Y→X是满射,故h:X→Y是单射.令p=h◦r,则X≅imp.类似定理2.3,根据(Y,e)是模糊Scott domain,容易证明imp是模糊有界完备domain.因此,(X,e)是模糊有界完备domain.
4 结束语
本文引入了模糊有界完备domain和模糊Scott domain的概念,研究了它们的模糊闭包算子的像以及模糊保序映射等一些基本的性质.证明了在相应条件下,IL(X)是模糊Scott domain,在此基础上给出了模糊有界完备domain的等价刻画.然而,模糊有界完备domain范畴和模糊Scott domain范畴是否是笛卡尔闭的,以及如何刻画它们的模糊Scott拓扑等方面的工作,可以进一步探究.

