n-余挠同调维数
熊 涛, 王芳贵, 王 茜
(1.西华师范大学 数学与信息学院,四川 南充637002; 2.四川师范大学 数学科学学院,四川 成都610066;3.四川文理学院 数学学院,四川 达州635000)
本文恒设R是给定的环,对左R-模N,

代表N的平坦(resp.投射,内射)维数.用Fn表示平坦维数不超过n的R-模簇,用

表示R的整体(resp.弱整体)维数.对于未解释的概念和符号,参考文献[1-2].
模类={W∈M|对任意左R-模M∈Fn,都有(M,W)=0.}一直备受关注.Bass[3]证明了每个(左)R-模有投射盖当且仅当R是左完全环(等价地,每个平坦R-模是投射模).随着盖包理论的发展,Enochs[4]提出了平坦盖猜测(flat cover conjecture,FCC):每个R-模有平坦盖.此后,多篇文献讨论了平坦盖的存在性[5-7].2001年,借助于模簇(学者们称之为余挠模),Bican等[8]解决了“FCC”,即证明了结合环上每个模都有平坦覆盖和余挠包络.
按照同调理论的观点,Mao等[9]定义了模M的余挠维数cotR M和环R的余挠整体维数l.cot.dim.(R),并且证明了环R是左完全环当且仅当

文献[9]的推论7.2.7称环R是左完全环是指每个R-模都有投射盖.R称为左m-perfect[10]是指每个平坦模的投射维数不超过m,由文献[9]的推论7.2.6可知环R是左m-perfect当且仅当

回顾交换环R称为几乎完全环是指它的每个真商环是完全环.几乎完全整环(almost perfect domains),简称为APD.作为余挠模理论的推进,Lee[11]将整环上的称为弱内射模.Fuchs等[12]定义了整环上的模的弱内射维数和环的弱内射整体维数,并在文献[11]的引理3.6和文献[12]的推论6.4中证明了一个整环是APD当且仅当它的弱内射整体维数≤1.Salce[13]证明了一个几乎完全环或者是完全环,或者是APD.此外,没有找到关于整体弱内射维数为零的相关环的表述.Mao等[14]研究了任意环上的,并将其称之为n-余挠模.这实际上是对余挠模的进一步发展.借助n-余挠模,文献[14]的推论6.4刻画了环R的弱整体维数,证明了w.gl.dim(R)≤n当且仅当每个n-余挠模是内射的.Enochs等[15]借助1-余挠模刻画了Noether环,文献[15]的定理4.4证明了左右Noether环R的内射包E(R)是平坦模当且仅当每个1-余挠模M的平坦盖F(M)是内射的.此外,Mao等[16]定义了另外一种n-余挠模:R-模N称为n-余挠模是指对任意平坦R-模F,都有
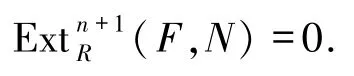
这2个概念是不一样的,见例1.

当且仅当
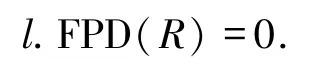
Vasconcelos[20]证明了一个交换环R是完全的当且仅当FPD(R)=0.
上述事实表明,R的l.FPD(R)维数与一种广义的-内射整体维数有着密切的联系,尤其是l.FPD(R)维数下的一维环和一维整环,从已有的研究结果来看,这种关系似乎更加密切.本文正是基于这种思想展开讨论的.
1 n-余挠模与n-余挠维数
容易看到,2种0-余挠模的定义是完全一致的,也就是余挠模.当n≥1时,文献[14-15]中定义的n-余挠模,都是文献[16]中定义的n-余挠模.但反之未必成立.
例1取环R=Z及模M=R/(2).由于

故R是文献[16]中定义的1-余挠模.同时,运用文献[21]的定理7.17可得到
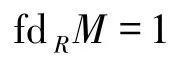
以及
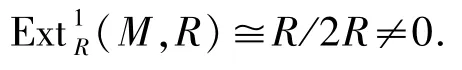
从而R不是文献[14-15]中定义的1-余挠模.
下文提及的n-余挠模,均是指文献[14-15]中定义的n-余挠模,并将该模簇记为Cn.
命题1对左R-模W,以下陈述是等价的:
1)W是n-余挠模;
2)对任意左R-模M∈Fn和任何整数k≥1,都有(M,W)=0;
3)如果正合列0→W→B→C→0满足C∈Fn,则它是分裂的;
4)如果正合列0→A→B→C→0满足C∈Fn,则序列

也是正合的.
证明1)⇔3)与2)⇒1)是显然的,1)⇔4)参考文献[14]命题4.4,下面只证1)⇒2).由定义有现在假设k>1.设0→A→F→M→0是正合列,这里F是投射左R-模,则


注意A∈Fn,故对k用归纳法,有

对R-模M的一个内射分解

记
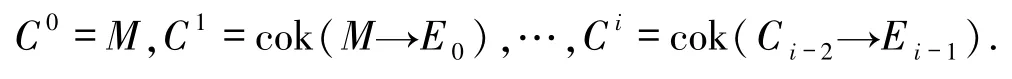
则第n阶上核Cn(n≥0)叫做M的第n阶上合冲.
文献[22]的定理2.2与文献[23]的引理5.5证明了对于整环R,R-模M满足fdRM≤1当且仅当对任意1-余挠模W,都有

以下定理是对模的平坦维数的更宽泛的讨论.
定理1设M是R-模.对任意n≥0,以下陈述是等价的:
1)fdRM≤n;
2)对任意0≤m≤n及任意m-余挠模N,成立;
3)对任意0≤m≤n及任意m-余挠模N及任意成立.
证明3)⇒2)是显然的,令m=n,由文献[14]的定理3.4即可得2)⇒1).下证1)⇒3).设W是N的(n-m)阶上合冲,由文献[14]中的命题4.3可知,W是n-余挠.由命题1即得,对于任意

对任意的n≥0,都有Cn⊇Cn+1.现在举出一个满足C0⊃C1⊃C2⊃…⊃Cn⊃…的环的例子.
例2取域F,构造环

这里x1,x2,…,x n,…是F上的未定元,则R是凝聚整环.对任意n≥1,记J= (x1,x2,…,x n),则由文献[24]的定理11.2.5可知
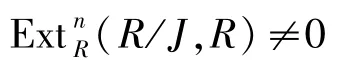
成立.设Cn-1是R的一个(n-1)阶上合冲,再由文献[24]中的定理11.2.5可知,Cn-1是(n-1)-余挠模,但不是n-余挠的.
定义1设M是R-模.M的n-余挠维数c nd RM是指使得序列这里对0≤i≤m,每个Wi是n-余挠模,是正合列的最小的非负整数m.如果不存在这样的m,则记

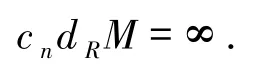
环R的n-余挠整体维数l.Cn.D(R)定义为l.Cn.D(R)=sup{c ndRM|M是任意R-模.}.
现在给出模的n-余挠维数的等价刻画.
定理2设m是非负整数.对R-模N,以下陈述等价:
1)c ndRN≤m;
2)对任意M∈Fn,

3)对任意M∈Fn和任意i≥1,

证明这是平凡的.
定理3设m是非负整数,则对环R,以下陈述等价:
1)l.Cn.D(R)≤m;
2)对任意的M∈Fn及N∈RM,

3)对任意的M,N∈Fn,

4)sup{c ndRN|N∈Fn}≤m;
5)sup{pdRM|M∈Fn}≤m.
证明5)⇔2)⇒3)是显然的,由定理2即可得1)⇔2)与3)⇒4).
4)⇒1) 设N∈RM,由文献[14]中的定理3.4,可得正合列

其中,F∈Fn,A∈Cn.对任意的左R-模M∈Fn,由命题1可得正合列

由定理2可得

故

2 对环的刻画
先来看什么时候每个n-余挠模是内射模.
定理4对环R,以下陈述等价:
1)w.gl.dim(R)≤n;
2)每个n-余挠模是内射的;
3)如果N∈Cn,则fdRN≤n;
4)对任意的M,W∈Cn,

成立.特别地,如果

则上述各条还与以下陈述等价:
5)对任意的W∈Cn∩Fn,W是内射的.
证明1)⇔2) 由文献[14]的推论6.4.
2)⇒4)和2)⇒5)是显然的,由定理1即可得4)⇒3).
3)⇒2) 设W是n-余挠模,且设
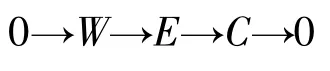
是正合列,这里E是内射模,则C是也是n-余挠的.由假设fdRC≤n,从而正合列是分裂的,故W是内射模.
5)⇒1) 用反证法.如果存在一个R-模满足其平坦维数超过n,不妨假设存在一个R-模M满足fdRM=n+1.由文献[14]的定理3.4可知,存在正合列
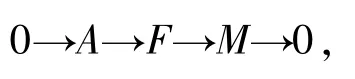
其中A是n-余挠的且满足

则

由假设,A是内射摸,从而给出的正合列是分裂的.因此,fdRM≤n.显然,这是一个矛盾,从而

推论1对环R,以下陈述是等价的:
1)R是Von Neumann正则环;
2)每个余挠模N是内射模;
3)每个余挠模N是平坦模;
4)对任意的余挠模M和N,
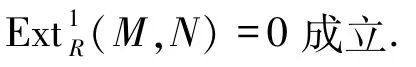
下面给出环R的l.Cn.D(R)维数与l.FPD(R)维数的关系.
定理5对任意环R,都有
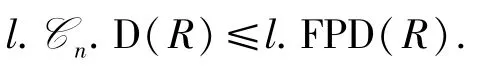
特别地,如果

则对任意的

证明设l.FPD(R)=k<∞且M∈Fn.由文献[25]中的命题6可知

故
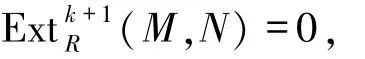
从而

如果
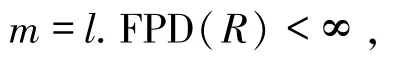
则存在一个R-模M满足

因此,存在一个R-模N满足
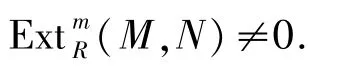
又因为M∈Fn和l.Cn.D(R)≥m,则

等价地,l.Cn.D(R)=l.FPD(R).
推论2设n≥1,R是环,有:
1)如果l.FPD(R)=0,则每个R-模是n-余挠的;
2)交换环R是完全环当且仅当每个R-模是n-余挠的.
下面研究左完全环与l.FPD(R)维数的关系.文献[3]定义了R的左弱finitistic维数:

引理1对环R,以下陈述是等价的:
1)l.FFD(R)≤n;
2)Fn+1=Fn;
3)Cn+1=Cn.
从而,l.FFD(R)=0当且仅当每个余挠左R-模是1-余挠的.
证明1)⇒2)⇒3)是显然,下面只证3)⇒1).设M是R-模满足

如果s>n,不失一般性,假设s=n+1.由条件可知,对任意n-余挠模W,

成立.由定理1可知

这是一个矛盾,故

即

定理6设n≥1.对环R,以下陈述等价:
1)l.Cn.D(R)=0,等价地,每个模是n-余挠模;
2)对任意模M∈Fn,M是投射的;
3)对任意模M∈Fn,M是n-余挠模;
4)R是左完全环且l.FFD(R)=0;
5)l.FPD(R)=0.
证明1)⇔2)⇔3) 运用定理3即可.而4)⇔5)是显然的.
1)⇔4) 运用文献[17]的命题3.3.1和引理1即可.
定义2称环R为左Cn-遗传环,即指:如果每个n-余挠模的商模是n-余挠的,等价于

定理7设n≥1,则对环R,以下陈述等价:
1)R是左Cn-遗传环;
2)对任意模M∈Fn,pdRM≤1;
3)任意模M∈Fn,c ndRM≤1;
4)每个内射模的商模是n-余挠模;
5)对任意R-模M,E(M)/M是n-余挠模,这里E(M)是M的内射包;
6)对任意R-模M,E(M)/M是n-余挠模,这里E(M)是M的n-余挠包;
7)每个投射R-模P的子模N∈Fn-1是投射模.
证明1)⇒4)和1)⇒6)⇒5)是显然的,而1)⇔2)⇔3)由定理3即得.
4)⇒1) 设0→N→W0→W1→0正合列,其中W0是n-余挠模.设E是W0的内射包.记

则可得如下行是正合列的交换图
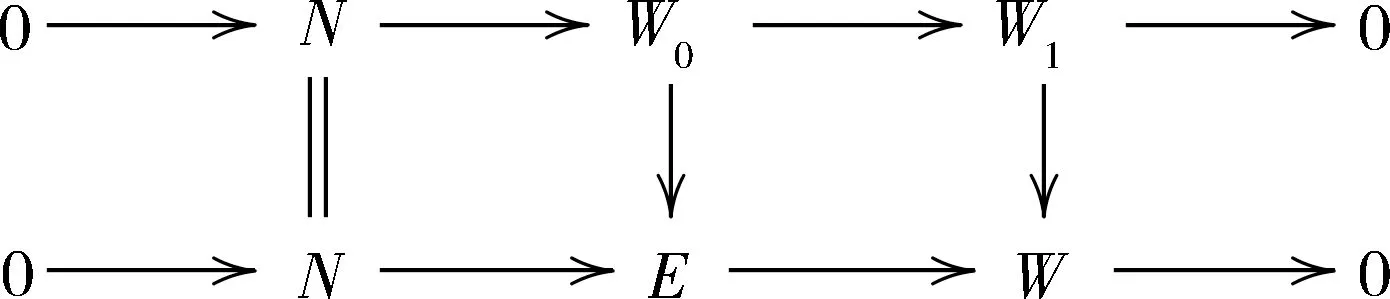
故

是正合的.对任意R-模N∈Fn,由假设可知

成立,故可由
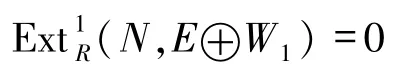
推出
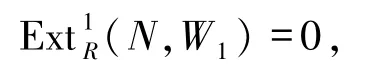
即W1是n-余挠的.
5)⇒4) 设0→K→E→C→0正合列,其中E是内射模.记E(K)⊆E是K的内射包,则存在R-模E0满足
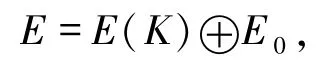
故

由假设可知,E(K)/K是n-余挠模,从而C是n-余挠模.
4)⇒7) 设P是投射R-模,N∈Fn-1是P的一个子模,且X是任意R-模,则存在正合列

其中,P/N∈Fn,E是内射模.由假设可知,C是n-余挠.对任意α∈HomR(N,C),考察如下行是正合列的交换图

则由命题1可知,存在 β∈HomR(P,C)满足

由于P是投射模,存在 γ∈HomR(P,E)满足
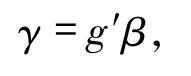
则
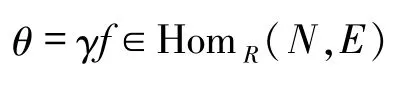
也满足
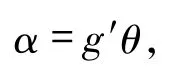
则

是正合列,则

因此,N是投射模.
7)⇒1) 设W是n-余挠R-模,N是W的子模.对任意的A∈Fn,存在正合列0→K→P→A→0,其中P是投射模且K∈Fn-1.由假设,K是投射模.对任意的 α∈HomR(K,W/N),考察如下行是正合列的交换图
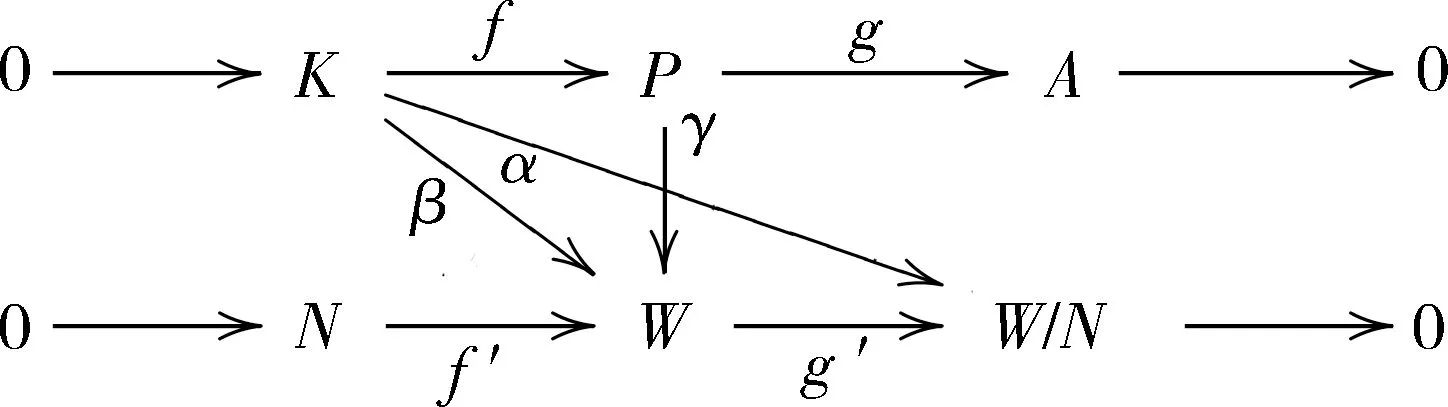
则存在同态

使得

由假设可知,W是n-余挠模且A∈Fn,则由命题1可知,存在同态
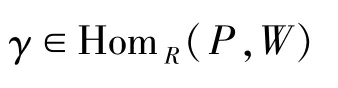
满足
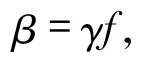
则

是正合列.由于

W/N是n-余挠模.
推论3对环R,以下陈述等价:
1)l.C1.D(R)≤1;
2)每个内射模的商模是1-余挠模;
3)每个投射模的平坦子模是投射的.
定理8设n>1,R是环,则以下陈述等价:
1)l.Cn.D(R)≤1;
2)l.C2.D(R)≤1;
3)l.FPD(R)≤1;
4)l.C1.D(R)≤1且l.FFD(R)≤1.
证明1)⇒2) 显然.
2)⇒3) 设M是R-模满足k:=pdRM<∞.如果k>1,则存在R-模N满足pdRN=2.由假设,pdRN≤1,这是一个矛盾,故k≤1.因此

3)⇒4) 如果M∈F1,则存在正合列
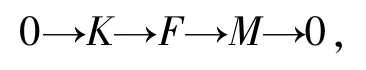
这里F是投射模,K是平坦模.由文献[25]的命题6可知
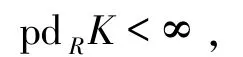
从而
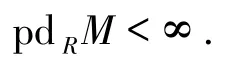
由假设,pdRM≤1,故K是投射模.因此

如果M∈F2,由定理7,fdRM≤pdRM≤1.因此,
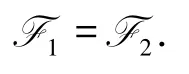
故由引理1可得

4)⇒1) 由于l.FFD(R)≤1,则C1=Cn.再次运用引理1可得

如下定理表明了左遗传环与左Cn-遗传环的差距.
定理9设n≥1,则对环R,以下陈述等价:
1)R是左遗传环;
2)R是左Cn-遗传环且w.gl.dim(R)≤1;
3)R是左C1-遗传环且w.gl.dim(R)≤1;
4)R是左Cn-遗传环且w.gl.dim(R)<∞;
5)R是左Cn-遗传环且w.gl.dim(R)≤n.
证明3)⇒1) 由定理4,每个1-余挠模是内射的,故R是遗传环.
1)⇒2)⇒3)和2)⇒4)是显然的,5)⇒1)类似于3)⇒1).下证4)⇒5).由上述讨论,当n=1是显然的.现在假设n>1.如果

则存在模M∈Fk.设B是M的第(k-n)阶合冲,则fdRB≤n.由定理7,fdRB≤pdRB≤1.因此

从而n≤1,这显然是个矛盾.从而k≤n,也就是说,w.gl.dim(R)≤n.
由文献[26]的定理90可知,一个Noether整环R是APD当且仅当dim(R)≤1,从而有:
定理10设R是Noether整环满足

证明由文献[27]可知

因此,由定理8,R是C2-遗传环.
由文献[11]的引理3.6及文献[12]的推论6.4可知,整环R是APD当且仅当R是C1-遗传整环.由文献[25]的命题6和文献[12]的推论,有如下推论.
推论4整环R是APD当且仅当

虽然整环R是C1-遗传环当且仅当R是APD,但C1-遗传环却未必是几乎完全环.
例3也可以举出C1-遗传环但不是几乎完全环的例子.事实上,设D是APD但不是域,则D不是完全环,从而R=D×D是C1-遗传环,则I=(D,0)≠0是R的理想.则D≅R/I是R的真商环,但不是完全环.因此,R不是几乎完全环.
致谢西华师范大学2017年度博士科研启动专项项目(17E087)对本文给予了资助,谨致谢意.

