具有低碰撞区的跳频序列的理论界

唐小虎

（西南交通大学 信息科学与技术学院，四川 成都611756）

由于跳频扩频（FHSS）通信系统具有较强的抗干扰能力、较高的保密性等特性，因而广泛应用于移动通信、短距离无线通信、军事无线通信等领域.对于跳频通信系统，使用跳频序列进行频移键控调制，使载波不断地进行跳变.汉明（Hamming）相关函数是两个跳频序列之间的一个重要特征，用来描述跳频序列在不同时隙频率重叠的总次数，是影响跳频通信系统性能的重要因素之一.跳频序列理论一直是现代扩频通信领域的重要研究课题.跳频序列理论包括跳频序列理论界与跳频序列设计两方面.跳频序列理论界是评价跳频序列集性能优劣的标准，对跳频序列设计具有重要的指导意义［1-7］.

根据跳频通信理论可知，为了降低多址干扰，跳频扩频序列的汉明相关函数应该具有如下“理想”特性：跳频序列除零时延外的全部自相关值和全部互相关值都应该是零.然而，由跳频序列理论界可以推出，“理想”跳频序列集的有关参数必须满足等式MN＝q，其中，N为跳频序列周期（长度）、M为跳频序列个数、q为跳频序列利用的频率数目［6］.在实际跳频扩频通信系统中，使用的跳频序列的长度总是大于频率数目，因而等式MN＝q总是不成立的，所以跳频通信系统一定存在用户间的多址干扰.

为了解决这些问题，必须创建一种新的研究思路，设计新型的跳频序列.首先考虑使用的一种思路是在“较小”的时延范围内分析跳频序列的汉明相关性.2006年，Peng等［8］提出低碰撞区跳频序列的新概念，将跳频序列的汉明相关函数自变量限制在零时延附近的一个小区间（LH）内进行研究.对于跳频序列集，当时延不超过LH时，如果每个跳频序列的汉明自相关值（零时延除外）和任意2个跳频序列的汉明互相关值都取很小的值（例如0、1、2等），则把这种跳频序列集称为“低碰撞区跳频序列集”，LH称为“低碰撞区（LHZ）”.特别地，当时延不超过LH时，如果每个跳频序列的汉明自相关值（零时延除外）和任意两个跳频序列的汉明互相关值都取0，则把跳频序列集称为“无碰撞区跳频序列集”，这样的LH称为“无碰撞区（NHZ）”，记为NH.很明显，对于低碰撞区跳频序列集，当时延不超过LH时，序列的汉明相关值较小，并且序列数目较多［8-9］.

自从低（无）碰撞区跳频序列的概念与研究方法被提出以后，尤其是首批研究成果公布报道以来，在国内外引起较大反响，许多学者开始投入低碰撞区跳频序列的研究，研究成果非常丰富，不断在国际期刊或国际会议发表出来.人们不但建立了一批低碰撞区跳频序列的理论界，而且构造出许多最优低碰撞区跳频序列集，推动了跳频序列理论的发展［10-26］.本文综合论述低碰撞区跳频序列理论界的研究状况.

1 具有低碰撞区的跳频序列周期汉明相关函数的理论界

在跳频通信系统中，发射机发送信号使用的频率是不断变化的，用跳频序列来描述这种变化规律.用F＝｛f1，f2，…，f q｝表示跳频通信系统使用频率的集合，其中q＝｜F｜表示频率的数目，把

x＝（x0，x1，…，x N－1），x i∈F，i＝0，1，…，N－1称为F上的一个跳频序列，其中N被称为跳频序列x的长度或周期.令S是由M个长度为N的跳频序列组成的集合.

对于任给2个频率f1，f2∈F，设

跳频序列的汉明相关函数是刻画跳频通信系统2个用户发送信号使用频率相互重叠的次数.

定义1.1［5］已知2个跳频序列

l为整数，0≤l＜N，把

称为跳频序列x和y关于时延l的周期汉明相关函数.式中的下标加法i＋l是按模N运算，并且这里只考虑正时延l.

已知跳频序列集S，把

称为S的最大周期汉明自相关边峰值，把

称为S的最大周期汉明互相关值.令

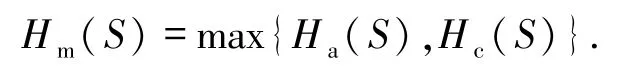
在不引起混淆的时候，简记

对于异步跳频通信系统，要求每对跳频序列在整个周期内无碰撞，可是根据跳频序列的理论界，这样的跳频序列的数目非常少，难以支持较多的用户.但是，如果将序列的汉明相关值限制在零时延附近的一个较小的时延范围内研究，就能够构造出较多的跳频序列.这就是低碰撞区跳频序列产生的基本思想.

下面给出低碰撞区跳频扩频序列的准确定义.

定义1.2［4，8］设S是由频率集F上的M个长度为N的跳频序列组成的集合，任给正整数

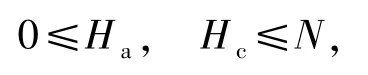
令

把LAHZ称为S关于周期汉明相关函数的自相关低碰撞区，LCHZ称为S关于周期汉明相关函数的互相关低碰撞区，LHZ称为S关于周期汉明相关函数的低碰撞区.进一步地，把S称为一个具有低碰撞区LHZ的跳频序列集，或者简称S是一个LHZ跳频序列集.

在定义1.1中，如果令

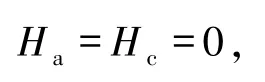
低碰撞区LHZ被称为跳频序列集S的一个无碰撞区，记为NHZ，同时把S称为一个具有无碰撞区NHZ的跳频序列集，或简称S是一个NHZ跳频序列集.

由定义1.1可知，完整描述一个低碰撞区跳频序列集S需要的参数有：跳频序列使用频率的数目q、跳频序列的长度N、序列的数目M、低碰撞区长度LHZ、在低碰撞区内的最大汉明自相关边峰值Ha和在低碰撞区内的最大汉明互相关值Hc.因此，可以把低碰撞区跳频序列集记为

类似地，无碰撞区跳频序列集具有4个参数，记为对于跳频通信系统，为了减少多址干扰，设计的跳频序列应该使其Ha和Hc尽可能小（例如Ha，Hc＝0，1或2等），使低碰撞区长度LHZ和序列个数M尽可能大.基于低碰撞区跳频序列的准同步跳频多址通信系统，只要相对时延不超过低碰撞区，序列之间的汉明相关值仍然是零或者是很小的值，能够有效地降低甚至消除系统的多址干扰.低碰撞区跳频序列在多用户雷达、声纳、蓝牙和超宽带等无线通信系统中具有重要的应用价值［25-30］.

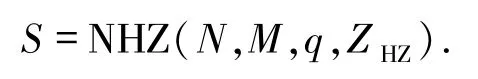
为了评价低碰撞区跳频序列的性能，必须揭示低碰撞区跳频序列集全部参数满足的数学关系.2003年，Ye等［9］首次给出了具有无碰撞区的跳频序列关于周期汉明相关函数的理论界.

定理1.1（Ye-Fan界）［9］设F是一个频率集，其元素个数为q，S是由F中M个长度为N的跳频序列组成的集合，NHZ是序列集S关于周期汉明相关函数的无碰撞区，则有

设a是一个实数，用表示小于或等于a的最大整数，用表示大于或等于a的最小整数.

2006年，Peng等［8］首次建立了具有低碰撞区的跳频序列关于周期汉明相关的理论界.

定理1.2（Peng-Fan-Lee界）［8］设F是一个频率集，其元素个数为q，S是由F中M个长度为N的跳频序列组成的集合，LHZ是S关于周期汉明相关函数的低碰撞区，令

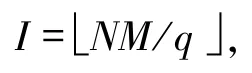
那么对于任意整数Z（0≤Z≤LHZ），有

注意到，Hm＝max｛Ha，Hc｝，由定理1.2可以得到如下推论.

推论1.1设F是一个频率集，元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，LHZ是S关于周期汉明相关函数的低碰撞区，令

那么对于任意整数Z（0≤Z≤LHZ），有

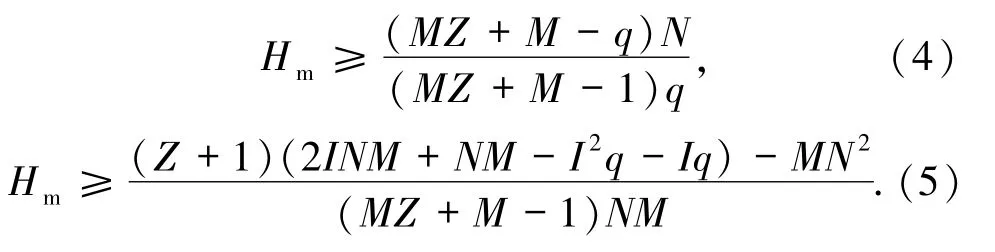
很明显，界（4）比界（5）更简洁，但由于

所以，界（5）比界（4）更紧.

在定理1.2中，令Ha＝Hc＝0，直接得到下面关于无碰撞区跳频序列的理论界.

推论1.2设F是一个频率集，其元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，NHZ是S的无碰撞区.令

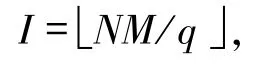
那么

可见，界（6）就是Ye-Fan界（1）.

现在将界（7）进一步简化，得到如下结果.

推论1.3设F是一个频率集，元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，NHZ是S的无碰撞区，那么

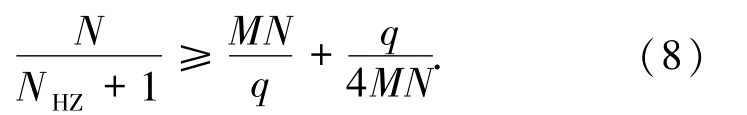
证明把界（7）变形为

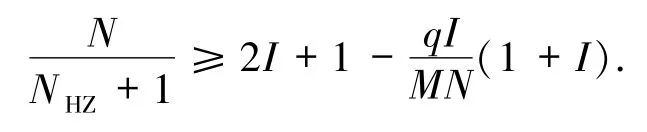
设

代入上式得

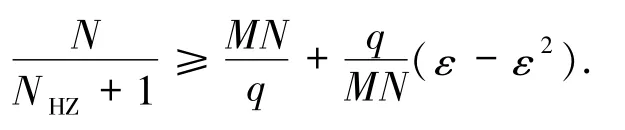
当0≤ε＜1时，有

所以（8）式成立.

界（6）可以变形为可见，界（8）比界（6）更紧.

定理1.2开创了低碰撞区跳频序列研究的新方向，从此以后，有关低碰撞区跳频序列的理论界与序列设计的研究成果不断被报道.2011年，Ye等［31］进一步改进了无碰撞区跳频序列关于周期汉明相关的理论界，获得了以下结果.

定理1.3（Ye-Fan界）［31］设F是一个频率集，其元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，NHZ是序列集S关于周期汉明相关的无碰撞区，则有

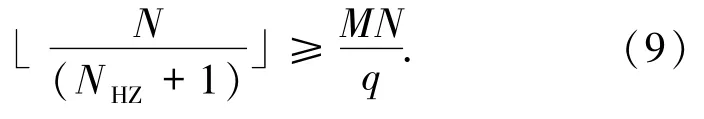
2019年，Liu等［15］建立了一个新的低碰撞区跳频序列关于周期汉明相关的理论界.

定理1.4（Liu-Shu-Zeng界）［15］设F是一个频率集，元素个数为q，S是由F中M个长度为N的跳频序列组成的集合，LHZ是序列集S关于周期汉明相关函数的低碰撞区.那么

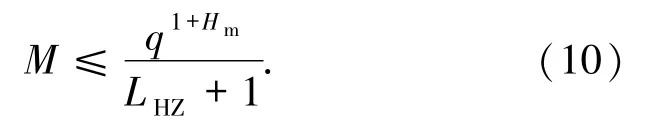
在定理1.4中，令LHZ＝N－1，可以得到常规跳频序列集周期汉明相关函数新的理论界.

推论1.4设F是一个频率集，元素个数为q，S是由F中M个长度为N的跳频序列组成的集合，那么

2 具有低碰撞区的跳频序列非周期汉明相关函数的理论界

跳频序列的非周期汉明相关函数是描述跳频通信系统频率碰撞的又一个重要指标，它的定义如下.

定义2.1已知2个长度为N的跳频序列

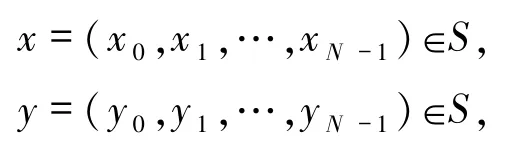
l为整数，且0≤l＜N，跳频序列x和y关于时延l的非周期汉明相关函数定义为

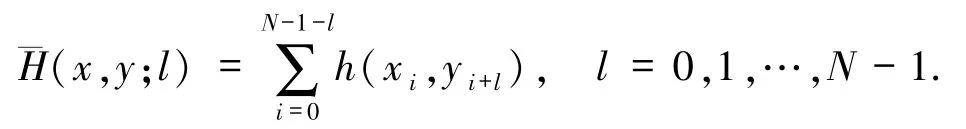
已知跳频序列集S，把

称为S的最大非周期汉明自相关边峰值.把

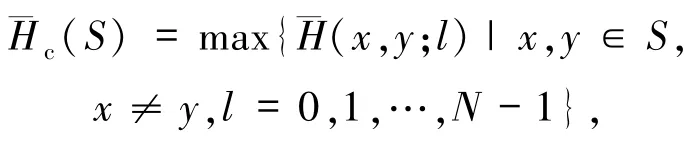
称为S的最大非周期汉明互相关值.设

为了简便，令

现在给出跳频序列集非周期汉明相关函数低碰撞区的概念.

定义2.2已知跳频序列集S，令整数a≥0，c≥0，那么，S关于非周期汉明相关函数的自相关低碰撞区LAAHZ、互相关低碰撞区LACHZ与低碰撞区LAHZ分别定义如下：

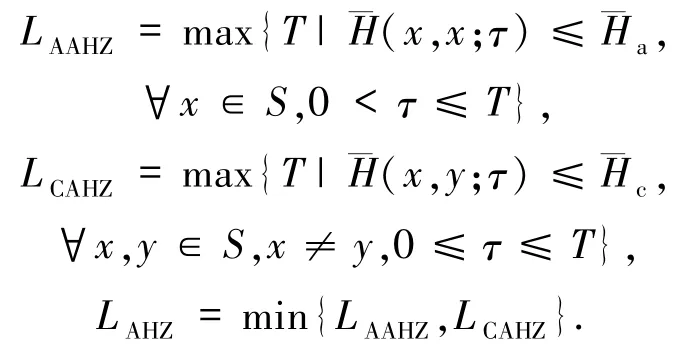
2010年，Niu等［20］首次给出了具有低碰撞区跳频序列集的非周期汉明相关函数的理论界.

定理2.1（Niu-Peng-Liu界）［20］设F是一个频率集，其元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，LAHZ是序列集S关于非周期汉明相关函数的低碰撞区.那么，对于任意整数Z（0≤Z≤LAHZ），有

推论2.1设F是一个频率集，其元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，LAHZ是序列集S关于非周期汉明相关函数的低碰撞区.那么，对于任意整数Z（0≤Z≤LAHZ），有

在定理2.1中，令

可以得到常规跳频序列集非周期汉明相关函数一个新的理论界.

推论2.2设F是一个频率集，元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，则有

推论2.3设F是一个频率集，其元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，则有

容易验证，理论界（14）与（15）比早期的常规跳频序列集非周期汉明相关的Peng-Fan界更紧［5］.2015年，Han等［23］得到了低碰撞区跳频序列集关于非周期汉明相关理论界的如下结果.

定理2.2（Han-Peng-Liu界）［23］设F是一个频率集，其元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，LAHZ是序列集S关于非周期汉明相关函数的低碰撞区.对于任意整数Z（0≤Z≤LAHZ），有如下结论.

当0≤Z≤min（LAHZ，N－a）时，有

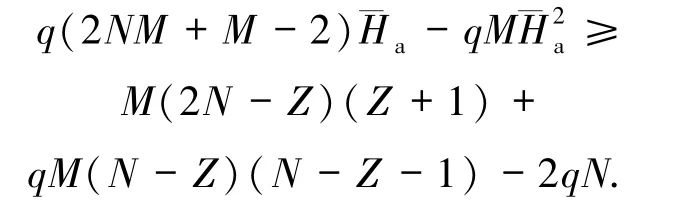
当0≤Z≤min（LAHZ，N－a）时，有

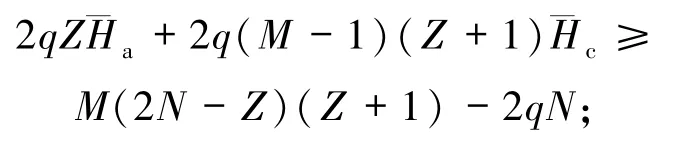
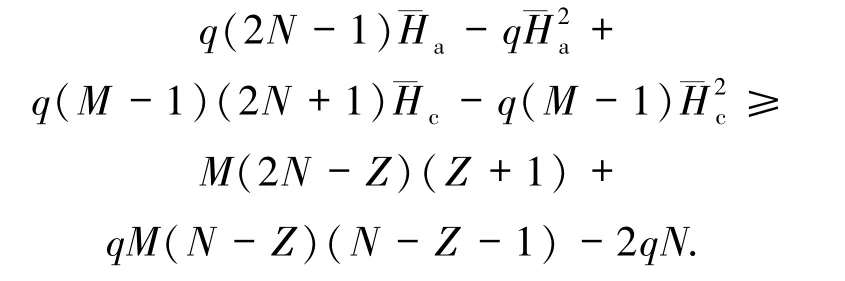
2018年，Liu等［32］得到了无碰撞区跳频序列集关于非周期汉明相关的一个新理论界.

定理2.3（Liu-Zhou-Zeng界）［32］设F是一个频率集，元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，NAHZ是序列集S关于非周期汉明相关函数的无碰撞区，则有

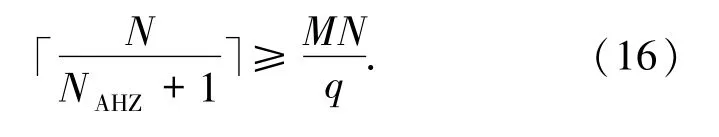
3 具有低碰撞区的跳频序列部分汉明相关函数的理论界

跳频序列的部分汉明相关是在一个比序列周期“更小”的时延范围内考虑序列的汉明相关特性.在实际应用中，部分汉明相关比全周期汉明相关能更准确地描述跳频通信系统的干扰特性.由于跳频序列部分汉明相关的数学描述比较复杂，研究比较困难，所以，在很长时间内，公开报道的研究结果较少.近年来，引入了跳频序列低碰撞区的概念，为跳频序列部分汉明相关函数理论研究提供了一种新方法，从而获得了一系列新的研究结果.

首先给出跳频序列周期部分汉明相关函数的概念.

定义3.1［5，16］设F是一个频率集，元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，对于任意两个跳频序列

序列x和y在相对时延为τ，相关窗起点为j，相关窗长度为L时的周期部分汉明相关函数定义为

其中，下标i＋τ按模N运算.当x＝y时，

被称为周期部分汉明自相关函数；当x≠y时被称为周期部分汉明互相关函数.明显地，如果令j＝0并且L＝N，周期部分汉明相关函数与周期汉明相关函数一致.进一步地，把

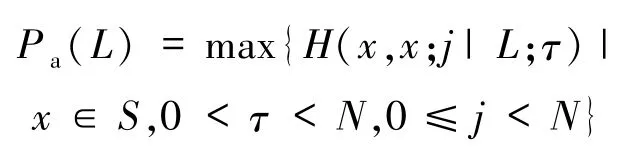
称为跳频序列集S的最大周期部分汉明自相关.把

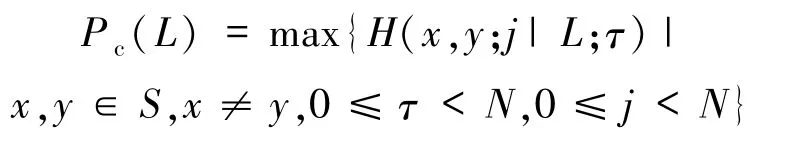
称为跳频序列集S的最大周期部分汉明互相关.把

称为跳频序列集S的最大周期部分汉明相关.在不引起混淆的时候，令

现在定义跳频序列周期部分汉明相关函数低碰撞区的概念.

定义3.2设F是一个频率集，元素个数为q，S是由F中M个长度为N的跳频序列构成的集合.对于任意给定的相关窗L（L≤N），令正整数

把定义为跳频序列集S的部分汉明自相关低碰撞区，把

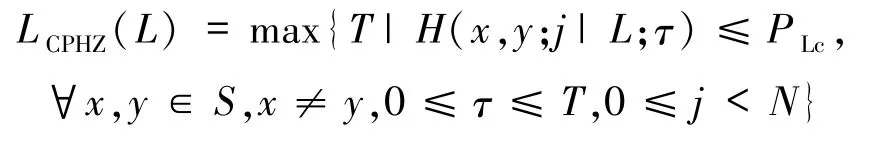
定义为跳频序列集S的部分汉明互相关低碰撞区，把

定义为跳频序列集S的部分汉明相关低碰撞区.

特别地，当j＝0且L＝N时，序列集S的周期部分汉明相关低碰撞区、周期部分汉明自相关低碰撞区和周期部分汉明互相关低碰撞区分别成为跳频序列集的周期汉明相关低碰撞区，周期汉明自相关低碰撞区和周期汉明互相关低碰撞区.为了简便，令LPHZ＝LPHZ（L）.

2018年，文献［18，33］首次建立了低碰撞区跳频序列集周期部分汉明自相关和周期部分汉明互相关理论界.

定理3.1［18，33］设F是一个频率集，元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，部分汉明相关窗长度为L（L≤N），LPHZ为S的周期部分汉明相关低碰撞区，令

那么对于任意正整数Z（0≤Z≤LPHZ），有

令PLm＝max｛PLa，PLc｝，由定理3.1立即得到以下推论.

推论3.1对于任意正整数Z，0≤Z≤LPHZ，令

有

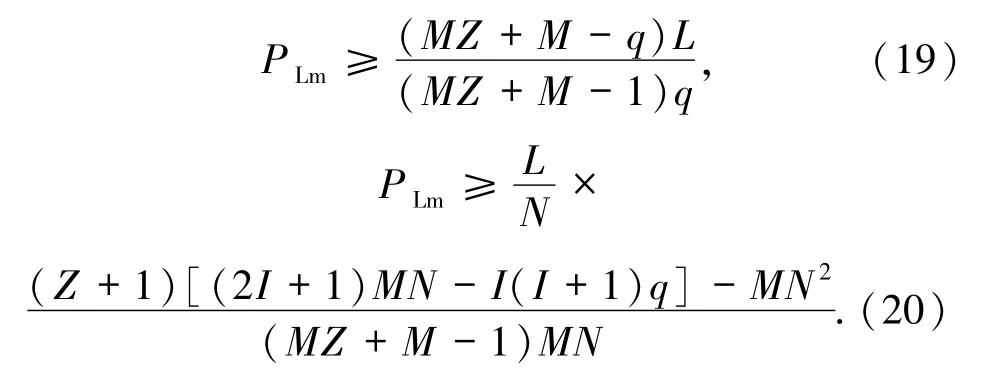
在定理3.1中，令L＝N，则跳频序列集S的周期部分汉明相关低碰撞区LPHZ即成为序列集S的周期汉明相关低碰撞区LHZ，可以直接导出低碰撞区跳频序列集周期汉明相关的理论界.

推论3.2设F是一个频率集，元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，LHZ为跳频序列集S的周期汉明相关低碰撞区.令

那么对于任意正整数Z（0≤Z≤LHZ），有

因此，界（21）和（22）分别是关于低碰撞区跳频序列周期汉明相关的Peng-Fan-Lee界（2）和（3）.如果令跳频序列集S的周期部分汉明相关低碰撞区Z＝LPHZ＝N－1，由定理3.1直接得出常规跳频序列集周期汉明相关的理论界.

推论3.3设F是一个频率集，元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，则有

可以看出，理论界（23）和（24）即是关于常规跳频序列周期汉明相关的Peng-Fan界［5］.在定理3.1中，令LPHZ＝N－1，可以得到常规跳频序列周期部分汉明相关的理论界［5］.

推论3.4设F是一个频率集，元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，相关窗长度为L（L≤N），令

则有

注意到Pm＝max｛Pa，Pc｝，可以直接得到以下推论.

推论3.5设F是一个频率集，元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，相关窗长度为L（L≤N），令

有

2017年，Zhou等［25］改进了界（20），获得了低碰撞区跳频序列集周期部分汉明相关一个新的理论界.

定理3.2（Zhou-Peng-Liang界）［25］设F是一个频率集，元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，相关窗长度为L（L≤N），LPHZ为跳频序列集S的周期部分汉明相关低碰撞区，令

那么对于任意正整数Z（0≤Z≤LPHZ），有

定理3.3（Zhou-Peng-Han界）［26］设F是一个频率集，元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，相关窗长度为L（L≤N），LPHZ为跳频序列集S的周期部分汉明相关低碰撞区.那么对于任意正整数Z（0≤Z≤LPHZ），有

容易检验，界（30）比界（19）更紧.2018年，Liu等［17］获得了低碰撞区跳频序列集周期部分汉明相关的一个理论界.

定理3.4（Liu-Zhou界）［17］设F是一个频率集，元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，相关窗长度为L（L≤N），LPHZ为跳频序列集S的周期部分汉明相关低碰撞区.那么对于任意正整数Z（0≤Z≤LPHZ），有

容易检验，界（31）比界（20）（29）更紧，并且与（20）（29）式相比较，（31）式更简洁，它不含参数I.在定理3.4中，令LPHZ＝N－1，直接得到常规跳频序列集周期部分汉明相关的理论界.

推论3.6设F是一个频率集，其元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，相关窗长度为L（L≤N），则有

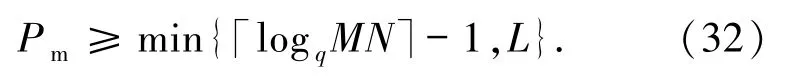
容易检验，界（32）比界（27）和（28）更紧.

4 具有低碰撞区的跳频序列汉明相关函数平均值的理论界

对于跳频序列的理论界，早期学者基本上都集中研究跳频序列汉明相关函数的最大值，这是从“最坏”的角度评估跳频序列的性能，根本原因还是数学描述比较容易.对于跳频扩频通信系统性能评估，跳频序列汉明相关函数的平均值也是一个重要的标准.但是，跳频序列汉明相关函数平均值的数学描述比较复杂，研究很难，一直未见有关研究结果.从2000年以来，彭代渊［4-5］开始研究跳频序列汉明相关函数平均值的理论界，不断有研究结果被发表出来.

首先给出跳频序列集平均汉明相关的有关定义.

定义4.1［5，34］设F是一个频率集，其元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，那么

和

分别称为跳频序列集S的周期汉明自相关碰撞总数和周期汉明互相关碰撞总数.将

和

分别称为跳频序列集S的平均周期汉明自相关和平均周期汉明互相关.在不引起混淆的时候，令

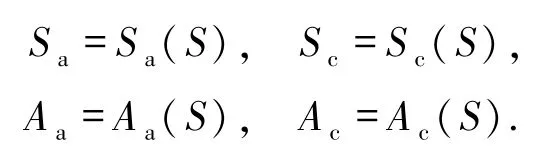
现在给出部分汉明相关函数平均值的定义.

定义4.2［5，35］设F是个频率集，其元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，相关窗长度为L（L≤N）.把

称为跳频序列集S在相关窗L内的周期部分汉明自相关函数总值，把

称为跳频序列集S在相关窗L内的周期部分汉明互相关总值.跳频序列集S在相关窗L内的周期部分汉明自相关函数平均值与周期部分汉明互相关平均值分别定义为：

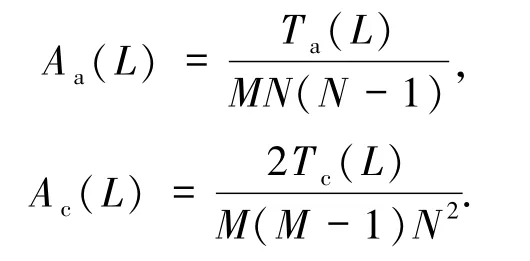
现在给出低碰撞区跳频序列集平均周期部分汉明相关的定义.

定义4.3［35-36］设F是一个频率集，其元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，相关窗长度为L（L≤N），LPHZ为跳频序列集S的周期部分汉明相关低碰撞区.对于任意正整数Z（0≤Z≤LPHZ），把

和

分别称为跳频序列集S在低碰撞区LPHZ内的周期部分汉明自相关总碰撞次数和周期部分汉明互相关总碰撞次数，并把

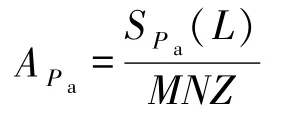
和

分别称为跳频序列集S在低碰撞区LPHZ内的平均周期部分汉明自相关和平均周期部分汉明互相关.2010年，Niu等［35-36］得到了具有低碰撞区的跳频序列集周期部分汉明相关平均值的理论界.

定理4.1（Niu-Peng-Liu界）［35-36］设F是一个频率集，其元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，相关窗长度为L（L≤N），LPHZ为跳频序列集S的周期部分汉明相关低碰撞区，令

那么对于任意正整数Z（0≤Z≤LPHZ），有

在定理4.1中，令j＝0，L＝N，则跳频序列集S的周期部分汉明相关低碰撞区LPHZ成为S的周期汉明相关低碰撞区LHZ，从而直接得到低碰撞区跳频序列集周期汉明相关函数平均值的理论界如下.

推论4.1［5］设F是一个频率集，其元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，S的周期汉明相关低碰撞区为LHZ，设

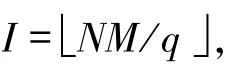
那么对于任意正整数Z（0≤Z≤LHZ），有

在定理4.1中，令Z＝LPHZ＝N－1，得到常规跳频序列集周期部分汉明相关平均值的理论界.

推论4.2［5］设F是一个频率集，其元素个数为q，S是由F中M个长度为N的跳频序列构成的集合，相关窗长度为L（L≤N），设

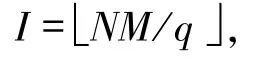
那么

5 具有低碰撞区的宽间隔跳频序列汉明相关的理论界

在有些无线通信应用中，要求实现宽间隔跳频，即要求在2个相邻跳频时隙里发射的2个载波的频率间隔大于某个规定的值.使用宽间隔跳频序列，有利于对抗窄带干扰、跟踪干扰与宽带阻塞式干扰［2］.首先给出宽间隔跳频序列的定义.

定义5.1［2，37］设F＝ ｛f1，f2，…，f q｝是一个频率集，f1＜f2＜…＜f q，x＝（x0，x1，…，x N－1）是F中长度为N的跳频序列，D是一个给定的整数，如果

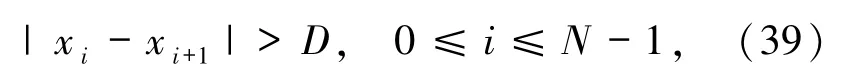
则称x是一个宽间隔跳频序列，并且把满足（39）式最小的D称为x的最小间隔.

2019年，Li等［37］首次得到了具有低碰撞区的宽间隔跳频序列集部分汉明相关的理论界.

定理5.1（Li-Fan-Yang界）［37］设F是一个频率集，其元素个数为q，S是由F中M个长度为N的宽间隔跳频序列构成的集合，部分汉明相关窗长度为L（1≤L≤N），LPHZ为S的周期部分汉明相关低碰撞区，令

那么

在定理5.1中，令部分汉明相关窗长度为L＝N，则跳频序列集S的周期部分汉明相关低碰撞区LPHZ即成为序列集S的周期汉明相关低碰撞区LHZ，可以直接得到具有低碰撞区的宽间隔跳频序列集周期汉明相关的理论界.

推论5.2设F是一个频率集，元素个数为q，S是由F中M个长度为N的宽间隔跳频序列构成的集合，LHZ为跳频序列集S的周期汉明相关低碰撞区，令

那么

在定理5.1中，令跳频序列集S的周期部分汉明相关低碰撞区LPHZ＝N－1，则直接导出宽间隔跳频序列集周期部分汉明相关的理论界.

推论5.2设F是一个频率集，其元素个数为q，S是由F中M个长度为N的宽间隔跳频序列构成的集合，部分汉明相关窗长度为L（1≤L≤N），令

那么

在推论5.2中令跳频序列集S的部分汉明相关窗长度为L＝N，则直接导出宽间隔跳频序列集周期汉明相关的理论界.

推论5.3设F是一个频率集，元素个数为q，S是由F中M个长度为N的宽间隔跳频序列构成的集合，令

那么

特别地，在（52）式中，令M＝1，得到一个长度为N的宽间隔跳频序列最大汉明自相关的理论界，那么

其中r＝Nmodq.

6 结论

跳频序列一直是扩频通信领域的基础理论研究课题.跳频序列理论包括理论界与序列设计2个方面.长期以来，跳频序列设计的研究成果很丰富，但跳频序列理论界的研究结果不多.直到本世纪初，我国学者提出了“低碰撞区跳频序列”的概念，并建立了相应的研究方法，为跳频序列的研究开创了一个新方向.从此开始，在国内外掀起了一股跳频序列的研究热潮，许多学者从事跳频序列理论的研究，大量研究成果被报道.文献［5］全面论述了常规跳频序列理论界的研究成果.本文完整地系统地阐述具有低碰撞区的跳频序列理论界的研究成果.可以看到，低碰撞区跳频序列理论界不但包含常规跳频序列理论界作为特例，而且得到了一些新的更紧的常规跳频序列理论界.

关于低碰撞区跳频序列设计的研究成果，将另外撰文论述.