二维空间中一类广义Zakharov系统爆破率的下界估计
孟令慧, 王 月
(天津大学 应用数学中心,天津300072)
1 引言与主要结果
本文考虑二维空间中一类广义Zakharov系统

系统(1)描述了冷等离子体中磁场的自生效应.(E1,E2)表示缓变高频电场的复振幅,n表示电子密度在其平衡位置的扰动[1-2].
赋予系统(1)初值:

对于经典的Zakharov系统

的有限时间爆破解的动力学行为的研究,已有了一些工作.特别地,Merle[3]研究了(3)式有限时间爆破解的爆破率的下界估计.对于系统(1),文献[4-6]研究了Virial型有限时间爆破解的存在性、非线性不稳定性及有限时间爆破解的爆破率的时空积分估计.文献[4]利用一个Virial型恒等式,采用极限方法得到如下结果.
命题1.1设(E10,E20,n0,v0)是关于x的径向对称函数,且H(E10,E20,n0,v0)<0,则初值问题(1)~(2)的解(E1,E2,n,v)(t,x)满足如下二择性结果:
(i)(E1,E2,n,v)(t)在空间H1(R2)×H1(R2)×L2(R2)×L2(R2)中有限时间爆破;
(ii)(E1,E2,n,v)(t)在空间H1(R2)×H1(R2)×L2(R2)×L2(R2)中无限时间爆破,即对任意时间t,(E1,E2,n,v)(t)有定义,且有

成立,其中H(E10,E20,n0,v0)由第2节(8)式给出.
受文献[3]的启发,本文将研究当爆破时间T<+∞时,(1)~(2)式的有限时间爆破解(E1,E2,n,v)(t)在t→T时,其在空间H1(R2)×H1(R2)×L2(R2)×L2(R2)中的范数
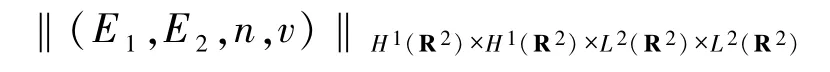
是以何种方式趋于无穷,即研究初值问题(1)~(2)的有限时间爆破解的爆破率的下界估计.
文献[5]在二维空间中构造了初值问题(1)~(2)在[0,T)上的一类爆破解,其形式如下:

本文将在二维空间中,研究系统(1)的有限时间爆破解的爆破率的下界估计,即如下主要结果.
定理1.2设(E1,E2,n,v)(t)是初值问题(1)~(2)的有限时间爆破解,且T为爆破时间,则存在仅依赖于初始值的常数

使得当t→T时,有
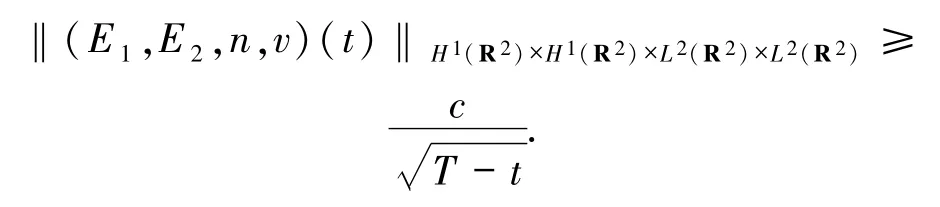
与经典的Zakharov系统(3)的相关结果相比,由于磁场效应的存在,即(1)式中非线性项包含这2项的存在给研究本文的相关问题带来了一定的困难.针对这些困难,通过对系统(1)做合适的尺度变换,并对磁场效应引起的相关项做恰当的先验估计,得到在能量空间中系统(1)的有限时间爆破解的爆破率的一致下界估计.
2 预备知识
由文献[2,4]可得柯西问题(1)~ (2)解的局部适定性理论.
命题2.1令初值

则柯西问题(1)~(2)在[0,T)上存在唯一解

且成立T=+∞或T<+∞,使得

此外,对任意t∈[0,T)成立如下的质量守恒和能量守恒:

其中
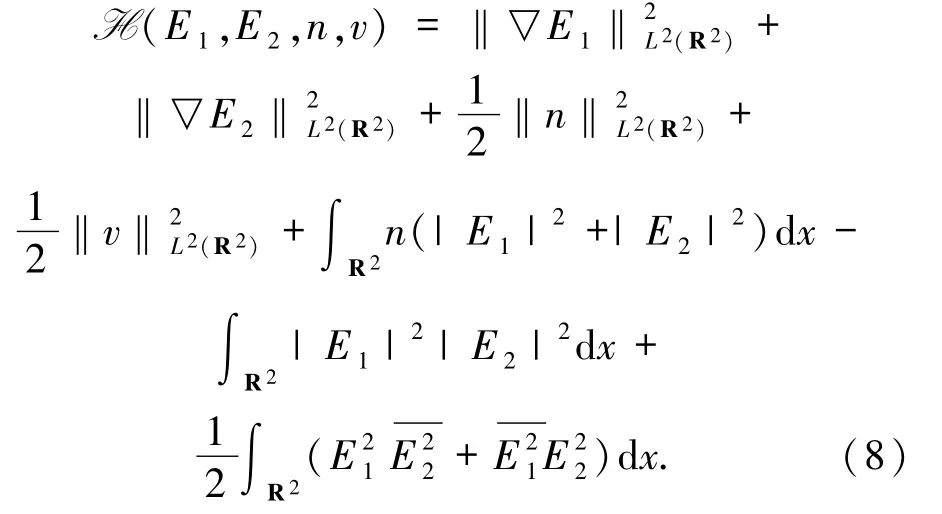
利用尺度变换,可得如下结论.
引理2.2对任意t∈[0,T),令
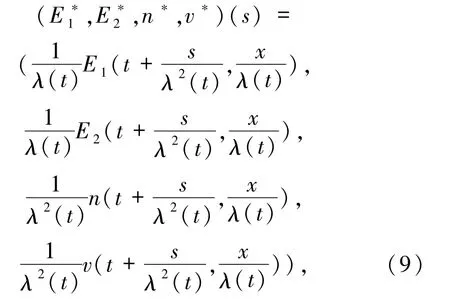
其中,s∈[0,λ2(T-t)),


此外,有如下结论成立:

证明直接计算可得引理2.2的结论.
引理2.3对任意s∈[0,λ2(T-t)),方程组(10)~(13)的解满足


其中,H如(7)~(8)式定义.此外,当t→T时,存在充分小的c>0,使得

证明利用引理2.2,直接计算可得(17)式.注意到,当t→T时,λ(t)→ + ∞,由此可知(18)式成立.
利用类似于文献[7]中的方法,可得如下结果.
引理2.4令 λ≥1且是方程组(10)~ (13)在[0,θ1]上的解,使得对任意s∈[0,θ1],有

且对于k≥2,有

则存在c>0,使得当s∈[0,θ1],有

令A(t)=eiΔt是自由Schrödinger半群,由文献[7]可得如下结果.
引理2.5对任意 φ(x)∈H1(R2),有:

由文献[8]可得如下引理.
引理2.6对任意u∈H1(R2),有如下结论成立

其中,Q是方程

的唯一径向正解.
3 主要结果的证明
定理1.2的证明首先,将证明当t→T时,方程组(10)~(13)的解在空间H1(R2)×H1(R2)×L2(R2)×L2(R2)中的范数一致有界,即如下结论成立.
命题3.1令λ≥1,且令存在常数c1>0使得

且

证明取 θ1>0,使得任意s∈[0,θ1],有:

其中,

β0>1是给定的一个充分大的常数.由引理2.4知,在[0,θ1]上有定义.
下证 θ1>θ2>0,其中 θ2仅依赖于常数c1.此证明分2步.
由(10)~(11)式知,对任意s∈[0,θ1]可得:

对任意s∈[0,θ1],由引理2.5可得:

注意到,由引理2.6可得:
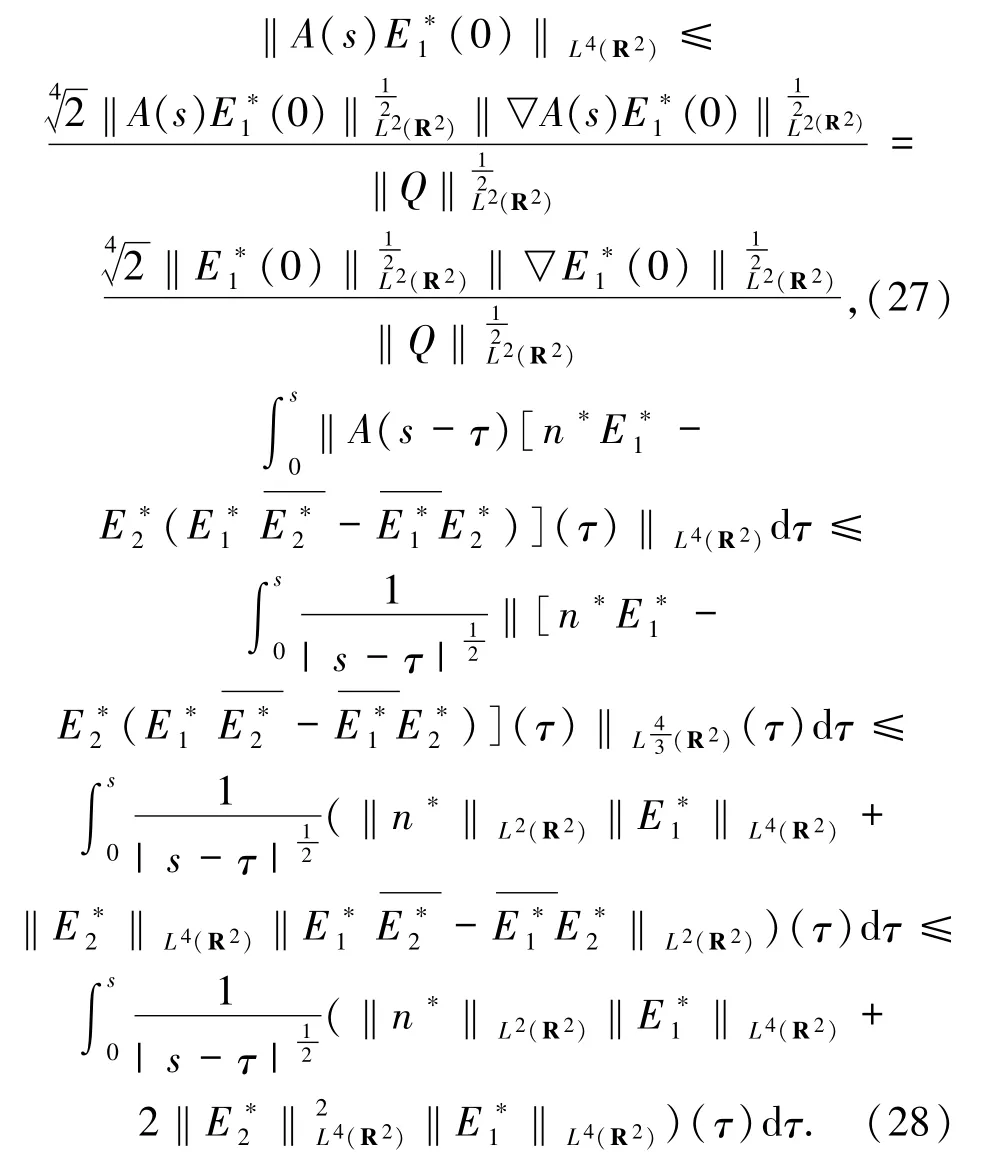
同理可得
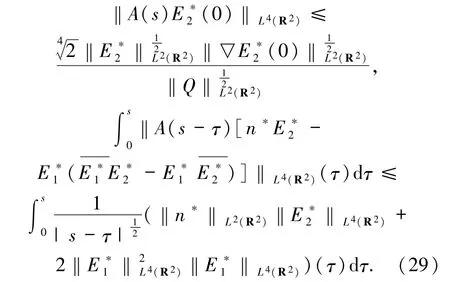
由(15)~(16)式知

于是,由(15)~(16)和(25)~(29)式知


其中,c0≥4.
第二步,估计

的一致上界.
另一方面,由引理2.3,(21)及(30)式知,对任意s∈[0,θ1]可得


其中,c*≥512.当t充分接近有限爆破时间T时,存在充分小的c3>0,使得于是,由(31)式可推知对任意s∈[0,θ1],有

于是,对任意s∈[0,θ2],有

由此,命题3.1得证.
注意到,当t→T时,λ(t)→ + ∞.于是,当t→T时,由命题3.1及(14)式知

于是,定理1.2得证.

