具有最优特性的一次碰撞跳频序列集的新构造

谢 春， 陈 平， 王常远， 彭代渊

(1. 成都工业学院 计算机工程学院 网络空间安全研究所 四川 成都 611730； 2. 四川省宜宾市翠屏区 建设工程安全服务站 四川 宜宾 644000；3. 宜宾学院 计算机与信息工程学院 四川 宜宾 644007)

0 引言

当前，信息技术在各行各业得到广泛应用，产生的信息安全问题日益突出，网络攻防[1-2]、密码学[3-4]、保密通信[5-6]等相关内容得到深入研究。跳频通信作为一种重要的保密通信方式，得到了广泛关注。在通信中，当多个用户在同一频隙同时通信时，便产生了影响通信性能的主要干扰，减小或消除通信中的各种干扰，实现保密、安全、可靠通信是十分必要的，跳频通信应运而生。跳频通信在蓝牙、军事通信以及移动通信中得到了广泛应用[5-7]，跳频通信中主要使用跳频序列来消除相关干扰，设计最优汉明相关特性的跳频序列具有重要的理论与应用价值。

一次碰撞跳频序列在全周期内具有最小的汉明相关值，其理论界以及最优跳频序列的设计得到了广泛研究。如：一次碰撞跳频序列理论界的建立以及序列构造[8-10]；基于笛卡尔积理论的构造[11]；一次碰撞跳频序列组合特征研究以及最优构造[12]；有限域上的构造[13-18]。本文利用有限域上的多项式理论，关于最大汉明相关值、平均汉明相关值、部分汉明相关值，构造一类具有新参数的一次碰撞跳频序列集，新跳频序列集在多个指标上均达到最优。

1 跳频序列汉明相关特性

本文中，将用到下面两个记号。

(N,M,q)-FHSS：由长度为N的M个序列组成的跳频序列集，其频隙个数为q。

(N,M,q,h) -FHSS：由长度为N的M个序列组成的、最大周期汉明相关值为h的跳频序列集，其频隙个数为q。

1.1 最大周期汉明相关

令D为定义在具有q个频隙的频隙集F上的跳频序列集(L,M,q)-FHSS。设u=(u0,u1,…,uL-1)与v=(v0,v1,…,vL-1)为D中的两个跳频序列，在时延τ时，u与v之间的周期汉明相关值PHu,v(τ)定义为

其中：如果uk≠v(k+τ)mod L，ph(uk,v(k+τ)mod L)=0；否则，ph(uk,v(k+τ)mod L)=1。

D的最大周期汉明相关值MH(D)定义为

针对单个跳频序列，Lempel和Greenberger[19]建立了最大周期汉明自相关值的理论界(L-G界)。

定理1若跳频序列的参数使L-G界中的等号成立，则该序列关于最大周期汉明自相关是最优的，若AH(s)-1使等号成立，则该序列关于最大周期汉明自相关是渐进最优的。

Peng等[7]建立了关于最大周期汉明相关值的理论界(Peng界_1)。针对最大周期汉明相关，Yang等[20]得到跳频序列集序列个数的理论上界(Yang界)。

定理2若跳频序列集D的参数使Peng界_1中的等号成立，则称D关于最大周期汉明相关是最优的；若Yang界中的等号成立，则称D的序列数目达到最优；若N+1使Yang界中的等号成立，则称D的序列数目是渐进最优的。

1.2 最大周期部分汉明相关

u与v在起点为j0、相关窗长度为w、时延为τ时的周期部分汉明相关值定义为

D的最大周期部分汉明相关值MPD(w)定义为

Zhou等[21]得到最大周期部分汉明相关值的理论界(Zhou界)。进一步地，Cai等[22]得到跳频序列集序列个数的上界(Cai界)。

定理3若对于所有相关窗长，跳频序列集D的参数使Zhou界中的等号成立，则称D关于最大周期部分汉明相关是最优的；若Cai界中的等号成立，称D的序列数目达到最优；若N+1使Cai界中的等号成立，则称D的序列数目是渐进最优的。

1.3 最大非周期汉明相关

u与v在时延τ时的非周期汉明相关值定义为

Liu等[23]建立了最大非周期汉明相关值的理论界(Liu界_1)。同时，Liu等[24]建立了跳频序列集序列数目的理论上界(Liu界_2)。

定理4若跳频序列集D的参数使Liu界_1中的等号成立，则称D关于最大非周期汉明相关是最优的；若Liu界_2中的等号成立，则称D关于序列个数是最优的；若N+1使Liu界_2中的等号成立，则称D的序列数目是渐进最优的。

1.4 平均周期汉明相关

跳频序列集D的平均周期汉明自相关值以及平均周期汉明互相关值分别定义为

对于跳频序列集D的参数L、N、AA(D)以及CA(D)，Peng等[25]建立了平均周期汉明相关值的理论界(Peng界_2)。

定理5若跳频序列集D的参数使Peng界_2中的等号成立，则D关于平均周期汉明相关是最优的。

跳频序列集D的平均周期部分汉明自相关值以及平均周期部分汉明互相关值分别定义为

Ren等[26]得到了跳频序列集平均周期部分汉明相关值的理论界(Ren界)。

定理6若跳频序列集D的参数使Ren界中的等号成立，则D关于平均周期汉明相关是最优的。

定理7若跳频序列集D关于平均周期汉明相关是最优的，则D关于平均周期部分汉明相关也是最优的，反之亦然。

2 一次碰撞跳频序列集的新构造

本节构造一类一次碰撞跳频序列集，并对其汉明相关特性进行分析。

令p为素数，有限域GF(p)上的一个跳频序列集Sa定义为

其中：k∈GF(p)。显然，跳频序列集的序列个数、序列长度以及频隙集大小均为p。接下来，将从最大非周期汉明相关、平均周期汉明相关、最大周期汉明相关、最大周期部分汉明相关4个角度分析Sa的特性。

2.1 最大非周期汉明相关

定理8关于最大非周期汉明相关理论界—Liu界_1，跳频序列集Sa是最优的。

证明令F(x)表示有限域GF(p)上的多项式，N(F)=N(F(x)≡0 modp)表示方程F(n)≡0 modp在有限域GF(p)内解的个数。对于Sa中的任意两个跳频序列u(i)、u(j)，其周期汉明相关值可表示为

其中：F(n)=2nτ+τ+τ2+j-i。

1) 当i≠j，τ取遍{0,1,2,…,p-1}中的数时，方程F(n)≡0 modp在有限域GF(p)内有唯一解n=(2τ)-1(i-j-τ-τ2)modp。

2) 当i=j，τ取遍{1,2,…,p-1}中的数时，方程F(n)≡0 modp在有限域GF(p)内有唯一解n=(2τ)-1(-τ-τ2)modp。当i=j，τ=0时，方程在有限域GF(p)内有p个解。所以

AH(Sa)=1，

Sa的最大周期汉明互相关值为

非周期汉明相关值可表示为

最大非周期汉明相关值为

则

因为

所以

进一步地

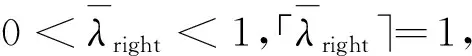
高血压合并心房颤动是心律失常最常见的类型之一，血压升高可增加房颤的发生风险，血压上升可增加左心室与左心房后负荷，导致心肌细胞肥大及间质纤维化，进而可导致心房电生理活动异常。由此可以看出，高血压与房颤的发生、发展及预后具有密切联系[3] 。

定理9针对最大非周期汉明相关，关于Liu界_2，跳频序列集Sa的序列个数是渐进最优的。

证明把相关参数代入Liu界_2中，右边的值为

所以，结论成立。

2.2 平均周期汉明相关

定理10关于平均周期汉明相关理论界—Peng界_2，跳频序列集Sa是最优的。

证明根据定理8的证明，对于任意i和j，有

则

AS(Sa)=p(p-1)；2CS(Sa)=p(p-1)2；

把相关参数代入Peng界_2的左边，可得

把相关参数代入Peng界_2的右边，可得

故结论成立。由定理7，可以得到定理11。

定理11关于平均周期部分汉明相关理论界—Ren界，跳频序列集Sa是最优的。

2.3 最大周期汉明相关

由定理8的证明可知，Sa的最大周期汉明相关值MH(Sa)=1。容易验证，关于最大周期汉明相关，Sa是最优的。

定理12跳频序列集Sa中每个跳频序列关于最大周期汉明自相关是渐进最优的。

证明把相关参数代入L-G界，右边的值为

显然，结论成立。

定理13针对最大周期汉明相关，跳频序列集Sa的序列个数是最优的。

证明把相关参数代入Yang界，右边为

显然，结论成立。

2.4 最大周期部分汉明相关

定理14关于最大周期部分汉明相关理论界—Zhou界，跳频序列集Sa是最优的。

证明设相关窗长为w，1≤w≤p，对于Sa中的任意两个跳频序列u(i)、u(j)，在起点为l的相关窗内的最大汉明相关值为

问题等价于n∈{l,l+1,l+2,…,l+w-1}，方程2nτ+τ+τ2+j-i≡0 modp解的个数。跳频序列集Sa的最大周期部分汉明相关值可表示为

对于任意相关窗长w，把相关参数代入Zhou界，右边的值为

所以结论成立。

定理15针对最大周期部分汉明相关，跳频序列集Sa的序列个数是最优的。

证明根据Cai界，对于任意相关窗长w，Cai界右边的值为

所以结论成立。

例根据本文的构造，可以得到有限域GF(13)上的跳频序列集，

y={y0={0,2,6,12,7,4,3,4,7,12,6,2,0};y1={1,3,7,0,8,5,4,5,8,0,7,3,1};

y2={2,4,8,1,9,6,5,6,9,1,8,4,2};y3={3,5,9,2,10,7,6,7,10,2,9,5,3};

y4={4,6,10,3,11,8,7,8,11,3,10,6,4};y5={5,7,11,4,12,9,8,9,12,4,11,7,5};

y6={6,8,12,5,0,10,9,10,0,5,12,8,6};y7={7,9,0,6,1,11,10,11,1,6,0,9,7};

y8={8,10,1,7,2,12,11,12,2,7,1,10,8};y9={9,11,2,8,3,0,12,0,3,8,2,11,9};

y10={10,12,3,9,4,1,0,1,4,9,3,12,10};y11={11,0,4,10,5,2,1,2,5,10,4,0,11};

y12={12,1,5,11,6,3,2,3,6,11,5,1,12}}。

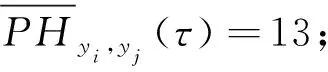
3 结束语

本文在有限域内，利用多项式构造一类一次碰撞跳频序列集，新序列集关于平均周期汉明相关、最大周期汉明相关、周期部分汉明相关是最优的，同时，针对特定汉明相关，序列个数达到最优。进一步构造具有最优汉明相关特性的跳频序列是下一步研究的重点内容。