非线性分数阶微分方程耦合系统解的存在性
周珏良, 何郁波, 谢乐平
(怀化学院 数学与计算科学学院 湖南 怀化 418008)
0 引言
分数阶微分系统的初边值问题具有深刻的科学背景。 与整数阶微分系统相比,分数阶微分系统能够更加精确地描述动态的变化过程[1-3],主要体现在对生物、物理、化学反应等方面。 近几十年,分数阶微分系统作为非线性分析的一个重要分支开始广泛应用于水动力学、生物力学、量子力学、控制论等领域,并取得了许多重要成果[4-11]。 与单个分数阶微分系统相比,耦合系统的研究条件更加复杂,因此关于分数阶微分耦合系统初边值问题的研究结果相对较少。
据我们所知,文献[12]利用格林函数和不动点定理在实空间中研究了非线性Riemann-Liouville型分数阶微分方程耦合系统边值问题解的存在性,之后又继续在实空间中研究下面非线性分数阶微分方程耦合系统边值问题解的存在性[13],
(1)
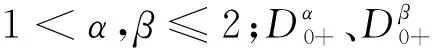
(2)
其中:1<α,β<2;0≤a,b≤1;0<ξ<1;Dα、Dβ是Riemann-Liouville型分数阶导数;f,g:[0,1]×[0,+∞)→[0,+∞)连续。 关于非线性分数阶微分方程耦合系统初边值问题的其他相关结论参阅文献[15-16]及其中的相关文献。 最近关于耦合系统的成果有董佳华等利用不动点定理在实空间中研究了一类非线性隐式分数阶微分方程耦合系统初值问题解的存在性和唯一性[17]。
受以上研究成果的启发,本文主要研究如下无限区间[0,+∞)上非线性Caputo型分数阶微分方程耦合系统在Banach空间中解的存在性和唯一性,
(3)
1 基本假设
给定本文所用到的空间
其中:λ>1,定义其范数
为了证明本文的结果,还需给定空间X×X={(x,y)|x∈X,y∈X},定义其范数为
‖(x,y)‖X×X=max{‖x‖X,‖y‖X}。
易证(X,‖·‖X)和 (X×X,‖·‖X×X)都是Banach空间[18-20]。
下面将给出本文所用到的假设条件。
H1) 连续函数x,y,trf(t,x,y):J×X×X→X,trg(t,x,y):J×X×X→X满足
‖tr[f(t,(1+tλ)x,(1+tλ)y)-f(t,(1+tλ)x′,(1+tλ)y′)]‖≤L1(t)‖x(t)-x′(t)‖+L2(t)‖y(t)-y′(t)‖,
‖tr[g(t,(1+tλ)x,(1+tλ)y)-g(t,(1+tλ)x′,(1+tλ)y′)]‖≤L3(t)‖x(t)-x′(t)‖+L4(t)‖y(t)-y′(t)‖,
其中:非负连续函数L1(t)、L2(t)、L3(t)、L4(t)满足
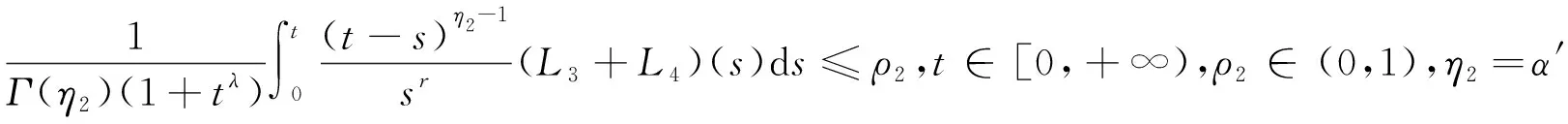
H2)存在常数M,N>0,使得f(t,0,0),g(t,0,0)满足
2 存在性结果
下面运用Banach压缩映射原理,证明初值问题(3)解的存在性和唯一性。
定理1假设条件H1)和H2)成立,则初值问题(3)的解存在且唯一。
证明定义算子T∶X×X→X×X,
显然算子T∶X×X→X×X。 事实上,对任意的(u,v)∈X×X,即u∈X,v∈X,有
另一方面,

‖u0‖+ρ1‖v‖X+M<∞,t∈[0,+∞)。
‖v0‖+ρ2‖u‖X+N<∞,t∈[0,+∞)。
因此可知T(u,v)∈X×X,故算子T∶X×X→X×X。
下面证明算子T∶X×X→X×X是严格压缩的。 事实上,对任意的u1,u2,v1,v2∈X,有
另一方面,我们有
由此可知,对任意的(u1,v1), (u2,v2)∈X,有
‖T(u1,v1)-T(u2,v2)‖X×X≤ρ‖(u1,v1)-(u2,v2)‖X×X,ρ=max{ρ1,ρ2}∈(0,1),
即算子T∶X×X→X×X是严格压缩的。
综上,根据Banach压缩映射原理得到算子T∶X×X→X×X在Banach空间X×X中存在唯一的(u,v),使得T(u,v)=(u,v),即问题(3)在Banach空间X×X中存在唯一解。
3 结论
本文通过构造特殊的Banach空间,运用Banach压缩映射原理得到了保证一类非线性分数阶微分方程耦合系统(3)在无限区间[0,+∞)上解的存在唯一性的充分条件。

