跳频序列研究综述

牛宪华，陈思利，王　瑜

(1. 西华大学计算机与软件工程学院， 四川 成都 610039; 2. 成都工业学院通信工程系，四川 成都 611730；

3. 成都航天通信设备有限责任公司，四川 成都 610666)



跳频序列研究综述

牛宪华1，陈思利2，王瑜3

(1. 西华大学计算机与软件工程学院， 四川 成都 610039; 2. 成都工业学院通信工程系，四川 成都 611730；

3. 成都航天通信设备有限责任公司，四川 成都 610666)

摘要：跳频通信中使用跳频序列来选择频点。跳频序列的理论界推导与序列设计是研究跳频序列的2方面。文章对跳频序列汉明相关函数和部分汉明相关函数在理论界和序列设计方面的国内外研究成果进行分析,指出低碰撞区跳频序列相关理论研究是未来研究的重点和难点内容之一，并预测具有最优部分汉明相关性能的低碰撞区跳频序列构造是未来发展的重要方向。

关键词：跳频序列；理论界；序列设计；汉明相关函数；部分汉明相关函数

跳频是一种通过控制频率跳变从而实现频谱扩展的扩频通信技术[1]。它具有难以截获、强抗干扰、支持多址组网、抗衰落、易与窄带通信系统兼容和良好的保密性等特点。跳频通信系统的这一系列突出优点，使其不仅在军事通信的电子对抗与反对抗中有广泛的应用，而且能满足民用通信的基本技术要求[2]。

在跳频通信系统中，跳频序列主要有2方面的作用：1)通过控制频率在不同频点快速跳变而扩展实际频率；2)跳频组网中的不同用户各自使用不同的跳频序列，防止多个用户占用同一个频段进行通信。用户间的多址干扰由跳频序列间频率的重复次数(碰撞次数)决定。序列间频率的碰撞次数越多则用户间多址干扰就越大，碰撞次数越少多址干扰越小。跳频序列的汉明(Hamming)相关性能反映了序列间频率的碰撞次数，并且很大程度地决定了跳频通信系统的性能。

本文主要分析跳频序列2种汉明相关函数以及不同汉明相关在理论界和序列设计方面的研究现状。首先介绍跳频序列低碰撞区的概念，然后介绍跳频序列分析时主要使用的2个相关函数(汉明相关函数和部分汉明相关函数)并分别对这2种相关函数的现阶段研究结果进行分析，最后总结了跳频序列的研究意义，展望了跳频序列未来可研究方向。

1低碰撞区跳频序列

低碰撞区(low hit zone, LHZ)跳频序列是2003年被提出的一种具有特殊性质的跳频序列[3-4]。在准同步跳频码分多址(QS-FH-CDMA)通信系统中，在一定的时延范围内系统保持异步性，跳频序列在零时延附近区域(低碰撞区)的汉明相关性能决定了系统抗多址干扰的能力。

针对低碰撞区跳频序列集，当在给定时延范围[-Z,Z]内时，LHZ跳频序列集的汉明相关值(包括汉明自相关和汉明互相关)都控制在很小的水平。当在给定时延范围[-Z,Z]内，跳频序列集的汉明自相关和互相关值等于0时，称区域Z为无碰撞区(NHZ)。图1和图2分别为跳频序列低碰撞区和无碰撞区的示意图。

图1　低碳撞区跳频序列的汉明相关

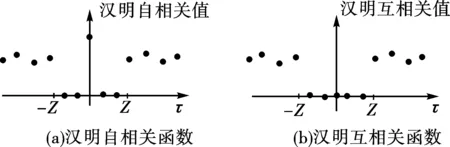
图2　无碰撞区跳频序列的汉明相关

2跳频序列的相关性

跳频序列的汉明相关性能是评价跳频序列性能的主要指标。根据跳频通信系统的要求，跳频序列集需具备以下特性[5]：

1)为减少系统不同用户间的多址干扰，跳频序列间的汉明互相关值应尽可能的小；

2)为提高跳频系统的同步性能，跳频序列的汉明自相关值应尽可能的小；

3)为提高跳频系统组网能力，使系统容纳更多用户，跳频序列集中的序列数目应尽可能多；

4)为使跳频系统具有良好的抗干扰性能，跳频序列应尽可能使用所有频隙且序列中的频隙应均匀分布；

5)为提高跳频系统的保密性，跳频序列应具有大线性复杂度和良好的随机性。

2.1跳频序列的汉明相关函数和部分汉明相关函数

跳频序列的汉明相关函数和部分汉明相关函数是研究跳频序列的汉明相关性能的主要指标。跳频序列的汉明相关函数刻画了不同用户序列在某时延下频点的碰撞情况。对跳频序列汉明相关函数的研究始于1974年，相关研究结果[6]较丰富。根据序列是否循环使用，汉明相关函数又分为周期汉明相关(序列循环使用)和非周期汉明相关(序列不循环使用)，如图3(a)和图3(b)所示。跳频序列部分汉明相关函数的概念由PN码中部分相关的概念转变而来。2004年， Eun等[7]开始对跳频序列部分汉明相关函数进行研究。部分汉明相关函数重点描述跳频序列局部的汉明相关性能，刻画了不同用户通信中实际使用的短序列在某时延下频点的碰撞情况。部分汉明相关函数定义了短序列的起点和相关窗长度，相关窗长度和起点位置可根据实际情况不断变化。当跳频序列的相关窗长度等于序列长度时，序列的部分汉明相关函数退化为汉明相关函数，所以序列的部分汉明相关函数将汉明相关函数作为它的特殊情况。跳频序列的部分汉明相关函数也可相应地分为周期部分汉明相关和非周期部分汉明相关，如图3(c)和图3(d)所示。

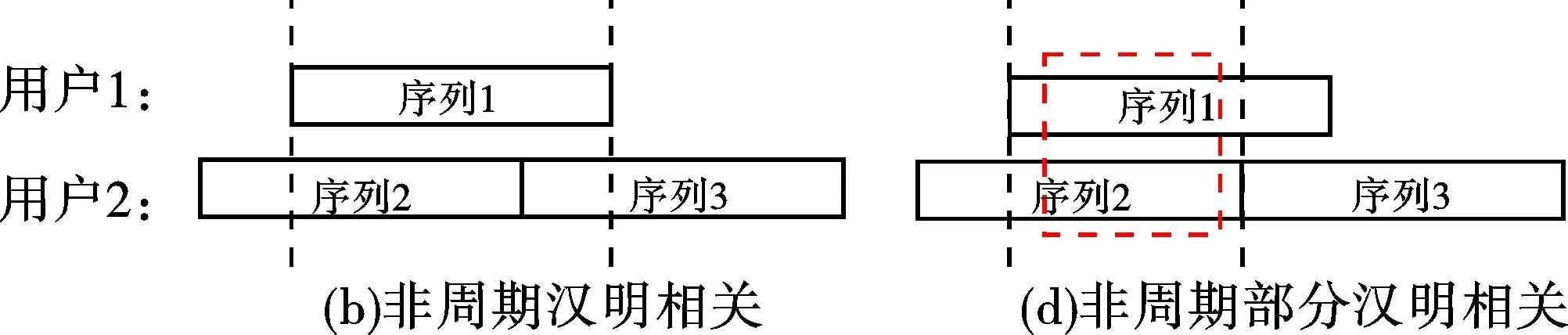
图3　跳频序列的汉明相关函数和部分汉明相关函数

现针对跳频序列汉明相关函数和部分汉明相关函数的国内外研究现状及发展动态进行简要分析。

2.2跳频序列汉明相关性能研究现状

跳频序列的长度、频点个数、序列个数以及汉明相关值的大小等参数之间有相互约束的关系，这些参数的约束关系即为理论界。跳频序列的理论界是指导跳频序列设计的重要标准，对评价序列性能有重要意义[1-2]。

下面列出几个重要的跳频序列汉明相关函数理论界研究结果：

1)1974年，Lempel等[6]首次得出跳频序列周期汉明自相关的理论界；

2)2003年，Ye等[3]首次导出NHZ跳频序列集周期汉明相关的理论界；

3)2004年，Peng等[8]得到了跳频序列集周期(非周期)汉明相关的理论界；

4)2006年，彭代渊等[9]得到了低碰撞区跳频序列集周期汉明相关的理论界；

5)2009年，Ding等[10]利用编码理论得到了跳频序列周期汉明相关的理论界。

跳频序列设计的任务就是构造满足相关理论界的跳频序列或跳频序列集，把满足理论界的跳频序列/跳频序列集称为关于该理论界最优的跳频序列/跳频序列集。近年来，国内外学者对跳频序列设计的研究十分活跃，并取得许多重要成果，已经设计出许多满足周期汉明相关理论界的最优跳频序列集。目前，有以下几类方法可以用来设计跳频序列。

1)基于有限域的多项式同余理论构造的一系列跳频序列具有良好周期汉明相关，且构造方法简单、易行；但由于序列数目不多且线性复杂度较小，难以满足系统需求。2010年，Niu等[11]建立了跳频序列平均周期汉明相关的理论界，研究了具有较大的序列个数的三次多项式跳频序列的平均汉明相关性质，其结果表明新序列集可以满足跳频码分多址系统的需求。2014年，Han等[12]基于多项式理论构造了一类具有新参数的最优跳频序列集。

2)基于具有理想自相关的p元序列已经构造了很多满足理论界的跳频序列集。1974年，Lempel等[6]基于GF(p)上的m序列，构造了最优跳频序列；1997年，梅文华等[13]基于GF(pn)上的GMW序列构造出最优跳频序列集； Udaya等[14]利用环上的迹函数，得到了2类不同的跳频序列集；在文献[15-16]中，香港科技大学丁存生教授和浙江大学葛根年教授基于指数和理论，进一步研究了利用有限域上的迹函数构造最优跳频序列集。

3)基于有限域上分圆技术构造跳频序列是近年提出的一种新方法。2005年， Chu等[17]首次使用分圆技术构造了最优跳频序列集；2008年，Ding等[15]基于分圆和离散对数得到一类最优跳频序列集；2010年，韩国Yang团队基于有限域的分圆技术，构造了几类最优以及几乎最优的跳频序列集[18]，并提出使用k级分圆技术来构造跳频序列集[19]；2013年，湖北大学曾祥勇教授等基于一种新的分圆类构造了一类新参数的最优跳频序列集[20]。

4)基于组合构造的方法构造跳频序列，也是近年出现的新方法。2004年以来，浙江大学葛根年教授和几位日本学者将组合数学的方法应用到跳频序列设计中，构造了一系列跳频序列集[16,21-22]。

5)基于编码理论构造跳频序列现在已经有很多结果。2010年，Ding等[23]使用线性循环码技术够造出一类跳频序列集；2011年，Yang等[24]结合截断Reed-Solomon码的特点构造了最优跳频序列集。

跳频序列的设计还有一些其他方法，相关研究结果如下。2010年，Chung等 (韩国Yang团队)[25]基于交织技术构造几类新的最优跳频序列集；2011年， Zhou等[26]给出一种利用差平衡函数构造跳频序列的一般方法；2012年， Zeng等[27]基于交织技术构造了具有新参数的最优跳频序列集；2012年，Zhou等[28]将不完全指数和理论应用于跳频序列的构造，研究了跳频序列的非周期汉明相关性质；2013年，Chung等 (韩国Yang团队)[29]基于非线性映射构造了几类新的最优跳频序列集。

近年，LHZ/NHZ跳频序列的设计也受到国内外学者的广泛关注。当前，低碰撞区跳频序列的研究已经出现了一些结果。2003年，汪晓宁等[30]基于现有的零相关区序列得到一类无碰撞区跳频序列；2007年，Ye等[31]利用矩阵变换的方法得到2类NHZ跳频序列集；2009年，Chung等 (韩国Yang团队)[32]利用交织技术构造了无碰撞区跳频序列集。但是现有的无碰撞区跳频序列的设计方法不能直接用于构造低碰撞区跳频序列，公开发表的低碰撞区跳频序列的理论界和序列构造的结果较少。2010年，西安电子科技大学的马文平教授等利用中国剩余定理首次构造了一类LHZ跳频序列集[33]；2012年，Niu等利用交织技术构造了几类具有灵活参数的LHZ跳频序列集[34]；2013 年，Niu等由单个跳频序列进行交织，构造了一类具有最优周期汉明相关的LHZ跳频序列集[35]；2013年，Chung等 (韩国Yang团队)基于笛卡尔积理论构造了一类最优LHZ跳频序列集[36]。

2.3跳频序列部分汉明相关性能研究现状

跳频序列的性能主要通过序列的汉明相关函数来衡量。在实际跳频通信系统应用中，由于硬件的复杂性以及同步时间的有限性，系统中实际使用的跳频序列并不一定是选择序列的全部，可能是一部分，即序列存在一个相关窗，且相关窗的长度通常小于所选序列的周期。另外，随着信道条件的变化，系统实际使用的跳频序列也不一定是从选择序列的第一个频点开始使用，即相关窗的长度会随之进行变化[1,37]。跳频序列的部分汉明相关函数考虑了相关窗长度以及位置的变化，是更为基本的序列性能。跳频序列的部分汉明相关函数能更好地描述跳频通信系统的性能。目前，已有的研究大多针对具有最优汉明相关性能的跳频序列，而对于具有最优部分汉明相关性能的跳频序列研究较少，因为后者难度更大，更具挑战性。

部分相关的概念最早用于研究PN码。2004年， Eun等[7]对跳频序列部分汉明相关性能进行了深入研究，将Lempel的理论界推广到部分汉明相关函数，建立了序列长度、频隙个数、相关窗长度及周期部分汉明自相关值之间的约束关系，首次得出了“单个跳频序列周期部分汉明自相关的理论界”。此理论界在相关窗长度等于序列长度时，将包含Lempel的理论界作为特殊情况。另外，Eun等在文中首次得出了具有最优部分汉明自相关的跳频序列。

跳频序列的部分汉明相关函数分析了跳频序列的部分汉明相关性能。近年来，关于跳频序列的部分汉明相关性能的研究已引起国内外学者的广泛关注。2010年，Niu等将Eun等的理论界推广到低碰撞区跳频序列集，建立了低碰撞区跳频序列集周期部分汉明相关的理论界[38]；2012年， Zhou等基于d-form函数，构造了一类具有最优周期部分汉明相关的跳频序列集[39]；2012年，Niu等又将有限域上的m序列和GMW序列扩展到多项式剩余类环上，构造了一类最优周期部分汉明相关的跳频序列集[40]；2014年，Liu等在文献[40]的基础上构造了一类最优周期部分汉明相关的低碰撞区跳频序列集[41]。2014年， Cai等构造了一类新参数的最优周期部分汉明相关的跳频序列集[42]。

3跳频序列的研究意义及未来可研究方向

根据前面章节的分析，可以看到，跳频序列的设计研究存在如下的问题。

1)低碰撞区跳频序列是跳频序列领域一个新的研究方向，已引起国际上许多学者的关注。目前，对无碰撞区跳频序列的研究已有较多结果，但由于低碰撞区跳频序列的特殊定义和性质，具有最优汉明自相关/汉明互相关的低碰撞区跳频序列/跳频序列集的研究结果较少；因此，低碰撞区跳频序列相关理论研究是未来跳频序列领域研究的重点和难点内容之一。

2)跳频序列的部分汉明相关性能比传统的汉明相关更为灵活，且对实际系统性能的影响不可忽视。目前对于具有最优部分汉明相关性能的跳频序列及低碰撞区跳频序列研究很少。如何构造具有最优部分汉明相关性能的低碰撞区跳频序列是今后研究的一个重要方向。

研究具有最优部分汉明相关的低碰撞区跳频序列设计方法，不但具有重要的理论意义，而且对于推动准同步跳频扩频通信系统的实际应用具有关键作用，对我国的民用无线电通信和军事抗干扰通信都将产生积极的影响。

参考文献

[1]Simon M K, Omura J K , Scholtz R A. et al. Spread Spectrum Communications Handbook[M]. New York: McGraw-Hill, 2002:352-359.

[2]梅文华, 王淑波, 邱永红.跳频通信[M].北京：国防工业出版社,2005:28-87.

[3]Ye W X, Fan P Z. Two Class of Frequency-hopping Sequences with No-hit Zone[C]//in Proceedings of the Seventh International Symposium on Communications Theory and Applications(ISCTA’2003). Ambleside, U K:[s.n.],2003:304-306.

[4]Wang X N, Fan P Z. A Class of Frequency Hopping Sequences with no Hit Zone[C]//in Proceedings of the Fourth International Conference on Parallel and Distributed Computing, Applications and Technologies, (PDCAT’2003). Chengdu: [s.n.], 2003:27-29.

[5]Fan P Z, Darnell M. Sequence Design for Communications Applications[M]. London: RSP-John Wiley & Sons Inc, 1996:271-350.

[6]Lempel A, Greenberger H. Families of Sequences with Optimal Hamming Correltaion Properties[J]. IEEE Transactions on Information Theory, 1974, 20(1):90.

[7]Eun Y C, Jin S Y, Hong Y P, et al. Frequency Hopping Sequences with Optimal Partial Autocorrelation Properties[J]. IEEE Transactions on Information Theory, 2004, 50(10):2438.

[8]Peng D Y, Fan P Z. Lower Bounds on the Hamming Auto-and Cross Correlations of Frequency-hopping Sequences[J]. IEEE Transactions on Information Theory, 2004, 50(9):2149.

[9]彭代渊, 范平志, 李门浩.低碰撞区跳频序列集周期Hamming相关函数的理论限[J]. 中国科学E辑:信息科学,2006, 36(2): 172.

[10]Ding C, Fuji-Hara R, Fujiwara Y, et al. Sets of Frequency Hopping Sequences: Bounds and Optimal Constructions[J]. IEEE Transactions on Information Theory, 2009, 55(7):3297.

[11]Niu X H, Peng D Y. Lower Bounds on the Average Partial Hamming Correlations of Frequency Hopping Sequences with Low Hit Zone[C]// Proc of the 6th International Conference on Sequences and Their Applications (SETA 2010). Paris, France:[s.n.],2010:67-75.

[12]Han H Y, Peng D Y. Set of Optimal Frequency-hopping Sequences Based on Polynomial Theory[J]. Electronics Letters, 2014, 50(3):214.

[13]梅文华, 杨义先.基于GMW 序列构造最佳跳频序列族[J].通信学报, 1997, 18(11):20.

[14]Udaya P, Siddiqi M U. Optimal Large Linear Complexity Frequency Hopping Patterns Derived from Polynomial Residue Class Rings[J]. IEEE Transactions on Information Theory, 1998, 44(4): 1492.

[15]Ding C, Yin J. Sets of Optimal Frequency-hopping Sequences[J]. IEEE Transactions on Information Theory, 2008, 54(8):3741.

[16]Ge G, Miao Y, Yao Z. Optimal Frequency Hopping Sequences: Auto-and Cross-Correlation Properties[J]. IEEE Transactions on Information Theory, 2009, 55(2): 867.

[17]Chu W, Colbourn C J. Optimal Frequency-hopping Sequences Via Cyclotomy[J]. IEEE Transactions on Information Theory, 2005, 51(3):1139.

[18]Han Y K, Yang K. On the Sidel’nikov Sequences as Frequency-hopping Sequences[J]. IEEE Transactions on Information Theory, 2009, 55(9):4279.

[19]Chung J H, Yang K. Optimal Frequency-hopping Sequences with New Parameters[J]. IEEE Transactions on Information Theory, 2010, 56(4):1685.

[20]Zeng X Y, Cai H, Tang X H, et al. Optimal Frequency Hopping Sequences of Odd Length[J]. IEEE Transactions on Information Theory, 2013, 59(5): 3237.

[21]Fuji-Hara R, Miao Y, Mishima M. Optimal Frequency Hopping Sequences: a Combinatorial Approach[J]. IEEE Transactions on Information Theory, 2004, 50(10): 2408.

[22]Ge G, Fuji-Hara R, Miao Y. Further Combinatorial Constructions for Optimal Frequency Hopping Sequences[J]. J Comb Theory Ser A, 2006, 113(8):1699.

[23]Ding C, Yang Y, Tang X H. Optimal Sets of Frequency Hopping Sequences from Linear Cyclic Codes[J]. IEEE Transactions on Information Theory,2010, 56(7):3605.

[24]Yang Y, Tang X H, Udaya P, et al. New Bound on Frequency Hopping Sequence Sets and its Optimal Constructions[J]. IEEE Transactions on Information Theory, 2011, 57(11):7605.

[25]Chung J H, Han Y K, Yang K. New Classes of Optimal Frequency-hopping Sequences by Interleaving Techniques[J]. IEEE Transactions on Information Theory, 2009, 55(12):5783.

[26]Zhou Z C, Tang X H, Peng D Y, et al. New Constructions for Optimal Sets of Frequency Hopping Sequences[J]. IEEE Transactions on Information Theory, 2011, 57(6):3831.

[27]Zeng X Y, Cai H, Tang X H. et al. A Class of Optimal Frequency Hopping Sequences with New Parameters[J]. IEEE Transactions on Information Theory, 2012, 58(7):4899.

[28]Zhou Z C, Tang X H, Yang Y, et al. A Hybrid Incomplete Exponential Sum with Application to Aperiodic Hamming Correlation of Some Frequency-hopping Sequences[J]. IEEE Transactions on Information Theory, 2012, 58(10):6610 .

[29]Chung J H, Yang K. A New Class of Balanced Near-perfect Nonlinear Mappings and its Application to Sequence Design[J]. IEEE Transactions on Information Theory, 2013, 59(2):1090.

[30]汪晓宁, 范平志.无碰撞区准同步跳频通信系统多址干扰性能分析[J]. 铁道学报, 2008, 30(5):125.

[31]Ye W X, Fan P Z. Construction of Frequency Hopping Sequences with no Hit Zone[J].Journal of Electronics(China) , 2007, 24(3):305.

[32]Chung J H, Han Y K, Yang K. Design of No-hit-zone Frequency-hopping Sequence Sets with Optimal Hamming Autocorrelation[C] //the Fourth International Workshop on Signal Design and its Applications in Communications (IWSDA’09).Fukuoka:IEEE, 2009:88-91.

[33]Ma W P, Sun S H. New Designs of Frequency Hopping Sequences with Low Hit Zone[J].Designs, Codes and Cryptography, 2010, 60(2):145.

[34]Niu X H, Peng D Y, Zhou Z C. New Classes of Optimal Low Hit Zone Frequency Hopping Sequence with New Parameters by Interleaving Techniques[J].IEICE Trans Fundamentals, 2012, E95-A(11):1835.

[35]Niu X H, Peng D Y, Zhou Z C. New Classes of Optimal Frequency Hopping Sequence Sets with Low Hit Zone[J].Advances in Mathematics of Communications, 2013, 7(3): 293.

[36]Chung J H, Yang K. New Classes of Optimal Low-hit-zone Frequency-hopping Sequence Sets by Cartesian Product[J]. IEEE Transactions on Information Theory, 2013, 59(1):726.

[37]Pursley M B, Sarwate D V, Basar T U. Partial Correlation Effects in Direct-sequence Spread-spectrum Multiple-access Communications Systems[J].IEEE Trans Comm, 1984, COM-32:567.

[38]Niu X H , Peng D Y, Liu F, et al. Lower Bounds on the Maximum Partial Correlations of Frequency Hopping Sequence Set with Low Hit Zone[J]. IEICE Trans Fundamentals, 2010, E93-A(11):2227.

[39]Zhou Z C, Tang X H, Niu X H, et al. New Classes of Frequency-hopping Sequences with Optimal Partial Correlation[J]. IEEE Transactions on Information Theory, 2012, 58(1):453.

[40]Niu X H, Peng D Y, Zhou Z C. Frequency/time Hopping Sequence Sets with Optimal Partial Hamming Correlation Properties[J].Science China, 2012, 55(10):2207.

[41]Liu X, Peng D Y, Han H Y. Low-hit-zone Frequency Hopping Sequence Sets with Optimal Partial Hamming Correlation Properties[J].Designs, Codes and Cryptography, 2014, 73(1):167.

[42]Cai H ，Zhou Z，Yang Y ，et al.A New Construction of Frequency-Hopping Sequences With Optimal Partial Hamming Correlation[J]. IEEE Transactions on Information Theory, 2014, 60(9):5782.

(编校：饶莉)

The Research Summary of Frequency Hopping Sequences

NIU Xianhua1，CHEN Sili2, WANG Yu2

(1.SchoolofComputerandSoftwareEngineering,XihuaUniversity,Chengdu610039China;2.DepartmentofCommunicationEngineering,ChengduTechnologicalUniversity,Chengdu611730China；3.ChengduAerospaceCommunicationDeviceCompanyLimited,Chengdu610666China)

Abstract:Frequency hopping sequence is utilized to choose the frequency slot in frequency hopping communication. The theoretical bounds and sequence design are the primary research aspects of frequency hopping sequence. Based on the Hamming correlation and the partial Hamming correlation of frequency hopping sequences, we investigated the domestic and foreign research results of the theoretical bounds and sequence design of frequency hopping sequence. We also pointed out that the bounds and constructions of low hit zone frequency hopping sequence with optimal partial Hamming correlation are important trends for future development.

Keywords:frequency hopping sequences；theoretical bounds；sequence design； Hamming correlation； partial Hamming correlation

doi:10.3969/j.issn.1673-159X.2016.02.005

中图分类号：TN914.41

文献标志码：A

文章编号：1673-159X(2016)02-0025-5

基金项目：国家自然科学基金青年基金(61401369)；教育部春晖计划(Z2014047) 。

收稿日期：2015-11-19

第一作者：牛宪华(1983—)，女，副教授，博士，主要研究方向为序列设计与分析，信息安全。E-mail：rurustef1212@gmail.com

·计算机软件理论、技术与应用·