基于分圆理论和中国剩余定理的最优平均汉明相关跳频序列集构造

蔡红斌，牛宪华，张秀杰

（西华大学计算机与软件工程学院，四川 成都 610039）

跳频通信系统的收发双方利用载波跳变实现频谱扩展。跳频系统因具有抗干扰能力优异、截获率低、抗衰落能力强等优点被广泛应用于无线电通信、现代雷达、声纳等电子系统[1]。在跳频通信系统中，控制载波频率跳变的伪随机码称为跳频序列。跳频序列的优劣对跳频系统的性能有着决定性的影响。跳频序列包含一些重要参数，如跳频序列集的频隙个数、周期长度、序列数目、序列的平均（最大）汉明自（互）相关值。通常要求跳频序列集具有如下特点：1)平均（最大）汉明自（互）相关值要尽可能低；2)序列数目尽可能多；3)各个频隙点出现的次数尽可能均匀；4)具有良好的随机性和较大的线性复杂度；5)易于实现。

跳频序列集的各参数之间相互约束，跳频序列理论界给出了不同参数之间应满足的约束关系。目前关于跳频序列理论界的研究已经取得了丰富的成果[2-5]。Lempel 等[2]给出单条跳频序列最大汉明自相关理论界；Peng 等[3]推导了跳频序列集最大汉明相关理论界。上述2 个理论界为构造最大汉明相关最优的跳频序列设计提供了理论基础。Peng 等[4]指出跳频序列的平均汉明相关可以衡量跳频通信系统的平均误差，更利于评价系统性能，并推导了平均汉明相关的理论界，然后基于多项式方法构造了一类满足平均汉明相关理论界的最优跳频序列集。Han 等[6]利用交织技术构造了一类满足平均相关理论界最优的跳频序列集。

分圆理论是构造最优跳频序列的有效工具。Chu 等[7]基于有限域Fp上的分圆理论得到了一类满足Peng-Fan 界最优的跳频序列集。Ding 等[8]基于有限域Fpn上的分圆，得到了一类具有新参数的最优跳频序列集。刘方等[9]基于广义分圆理论构造了一类满足平均汉明相关理论界最优的跳频序列集。柯品惠等[10]推广了广义分圆理论并构造了一类满足平均汉明相关理论界最优的跳频序列集。Zeng 等[11]基于环上的分圆，给出了一类具有灵活参数的跳频序列集。Xu 等[12]在文献[11]的基础上给出了一类最优跳频序列集的扩展构造。

本文基于分圆理论和中国剩余定理，构造了一类具有新参数的最优平均汉明相关跳频序列集，即根据中国剩余定理在文献[11]的基础上，得到一类序列长度更长且满足Peng-Liu-Tang 界的最优平均汉明相关跳频序列集。

1 预备知识

首先介绍本文中主要用到的一些符号。

1) 「a」：不大于a的最大整数。

2) 「a」：不小于a的最小整数。

3)v：，pi为素数，其中2 ＜p1＜p2＜ ··· ＜pk，mi是任意正整数。

4) (N,l,λ)：在大小为l的频隙集F上，序列长度为N且最大汉明自相关值是λ的跳频序列。

5) (N,l,λ;M)：在大小为l的频隙集F上，序列长度为N，序列数目为M，且最大汉明互相关值是λ的跳频序列集。

6)Zv={0,1,2,···,v-1}：一个有v个元素的模v剩余类环。

7)q：q=pn，p为任意奇素数。

8) ＜t＞n：t模n的最小非负剩余。

9)Fq：q元有限域。

10)Fq*：Fq中所有非零元的集合。

1.1 跳频序列基本概念

令F是一个大小为l的频隙集，S是定义在频隙集F上，长度为N的M条跳频序列构成的跳频序列集。对于S内任意2 条跳频序列xi={xi(0),xi(1),···,xi(N-1)}和xj={xj(0),xj(0),···,xj(N-1)}，0 ≤i，j≤M-1，在时延为τ时，其周期汉明相关函数定义为

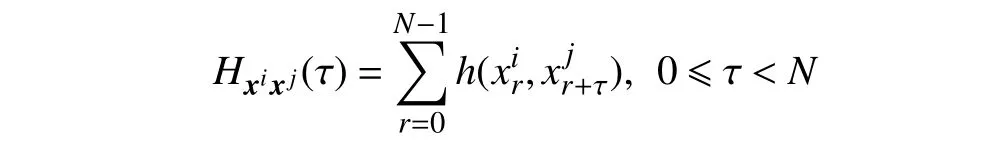
其中当a=b时，h(a,b)=1，否则，h(a,b)=0。下标r+τ 按模N运算。

对所有0 ≤r＜N，若=，则xi=xj，否则xi≠xj；若xi=xj，这种情况下称Hxixj(τ)为序列的汉明自相关函数；若xi≠xj，则称Hxixj(τ)为序列集S的汉明互相关函数。跳频序列集S的最大汉明自相关Ha(S)、最大汉明互相关Hc(S)和最大汉明相关H(S)定义为：

简记：λa=Ha(S)，λc=Hc(S)，λ=H(S)。

理论界是评价跳频序列（集）优劣性的一个重要指标，对序列设计起指导作用。

1974 年，Lempel 和Greenberger 给出了跳频序列周期汉明自相关理论界。

引理1[2] (Lempel-Greenberger 界)对于一个定义在大小为l频隙集F上，长度为N的跳频序列X，其最大汉明自相关满足

其中ε是N模l的最小非负剩余。

如果一个(N,l,λ)跳频序列X的最大汉明自相关满足不等式(1)的最小整数解，则称其为最优跳频序列。

2004 年，Peng 和Fan 给出了跳频序列集最大汉明相关理论界。

引理2[3] (Peng-Fan 界)设F是一个大小为l的频隙集，对于一个定义在频隙集F上的M个长度为N的跳频序列构成的跳频序列集S，其最大汉明相关满足

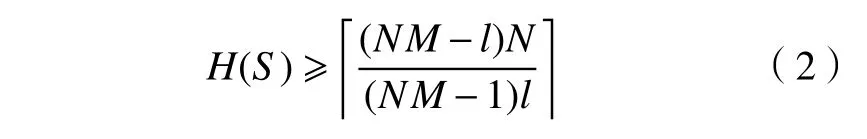
如果跳频序列集S的最大汉明相关是不等式(2)的最小整数解，则该跳频序列集可以被称作最优跳频序列集。

作为衡量跳频序列集性能的重要参数，跳频序列平均汉明自相关和平均汉明互相关的定义在2010 年Peng 等[4]给出。

定义1[6]设F是一个大小为l的频隙集，对于一个定义在频隙集F上的M个长度为N的跳频序列构成的跳频序列集S有

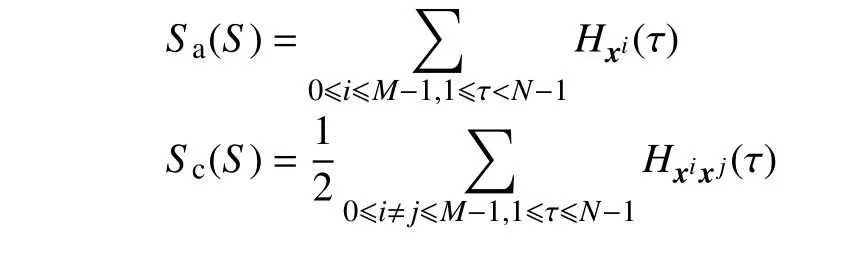
它们分别是序列集S的汉明自相关的总和、汉明互相关的总和。序列集S的平均汉明自相关和互相关分别是：

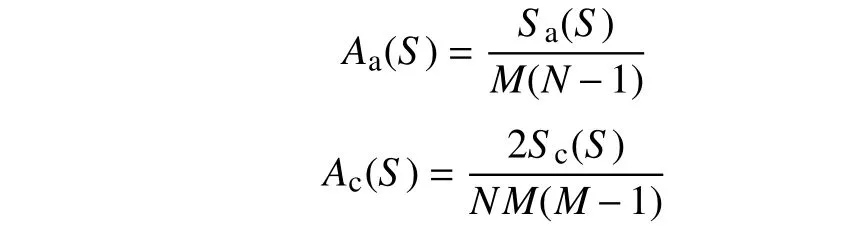
引理3[4]设F是一个大小为l的频隙集，对于一个定义在频隙集F上的M个长度为N的跳频序列构成的跳频序列集S，则有不等式

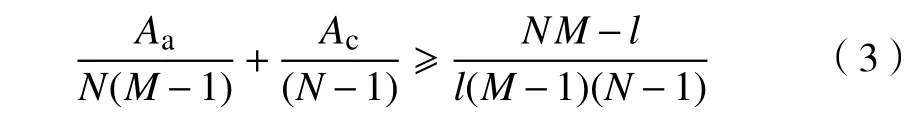
式中Aa和Ac分别是序列集S的平均汉明自相关和平均汉明互相关。如果跳频序列集S的平均汉明相关值满足不等式(3)的等号成立，则该跳频序列集可以被称为满足平均最优的跳频序列集。

推论1设F是一个大小为l的频隙集，对于一个定义在频隙集F上的长度为N的跳频序列X，有

推论1 的结果可以由文献[2]中引理4 得出。

1.2 有限域上的分圆

2008 年Ding 等[8]给出了有限域Fq上的分圆，本节将简单介绍有限域上的分圆理论。设q=pn=ef+1，其中p是一个素数，n是一个正整数，e＞ 1。设α是Fq的一个本原根，则Fq*可划分为一个e阶分圆类，该分圆类定义为

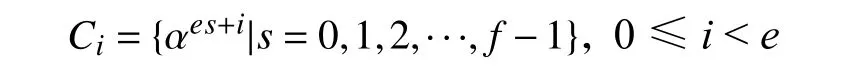
设对于正整数N，模N剩余类环ZN={0,1,2,···,N-1}。对于a∈ZN，令D为ZN的一个子集，定义

对于任意点x∈Ci，y∈Cj，0 ≤i≠j＜e，定义方程x-y=1 的解是e阶分圆类的e阶分圆数，对于任意i和j，也可将e阶分圆数表示为

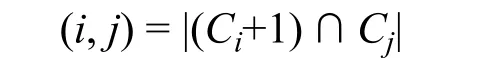
引理4定义的e阶分圆数具有如下基本性质：

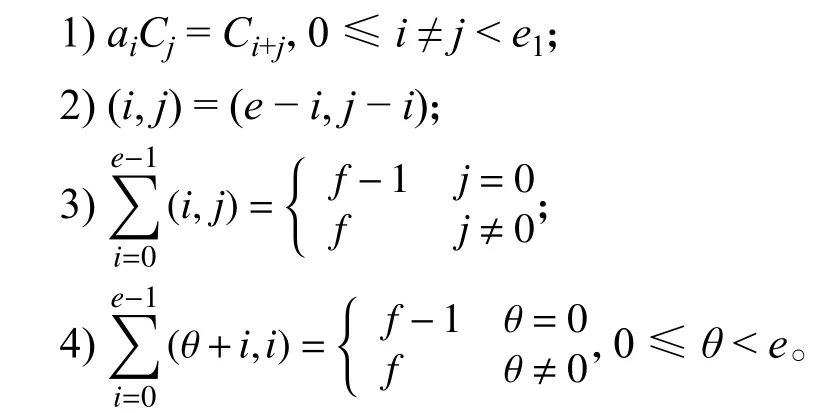
1.3 环上的分圆

2013 年，Zeng 等[11]给出了环上的分圆。

根据中国剩余定理可得：

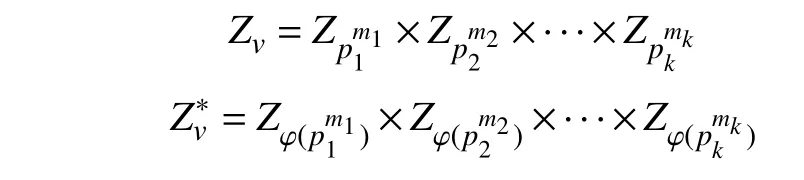
对于模v剩余类环Zv={0,1,2,···,v-1}，令A是Zv的一个子集，b是Zv中的一个元素，则有：

设v1表示v的一个因子，根据中国剩余定理，存在一个整数 ωv1满足模v1乘法阶是e1。定义D(v1)={|0 ≤d≤e1-1}，故可知D(v1)是的一个循环子群且阶为e1。

下面定义集合Ωv，为

引理5对于任意的v1,v1是v的一个因子，可知

2 跳频序列集的构造

本节基于环上的分圆理论和中国剩余定理给出了一类跳频序列集的构造，并证明了所构造的跳频序列集满足平均汉明相关理论界最优。

设n是一个正整数且n小于v。由中国剩余定理可知，当n不能被v整除时，Znv中任意一元素h,都可写成Zn×Zv中的一个元素(h1,h2),其中h1=＜h＞n,h2=＜h＞v。

基于环上分圆的性质，可以给出新的跳频序列集的构造方法。

定理1根据构造方法构造的跳频序列集有如下性质。

1）构造得到跳频序列集的序列长度为n(v-1)，频隙点个数为，跳频序列集S平均自相关和互相关总和分别是：

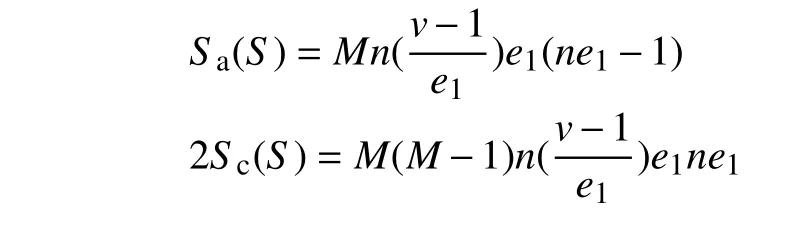
2）由构造得到的跳频序列集S满足平均汉明相关理论界最优。

证明1) 定义＜τ1＞n,＜τ2＞v-1，xs，xr是跳频序列集S里任意2 条序列

为求2 条序列的汉明相关性，将上面讨论的结果τ1,τ2的取值分成4 种情况考虑。

情况1，当τ1=0，τ2=0 时，由g是二元单射,得到

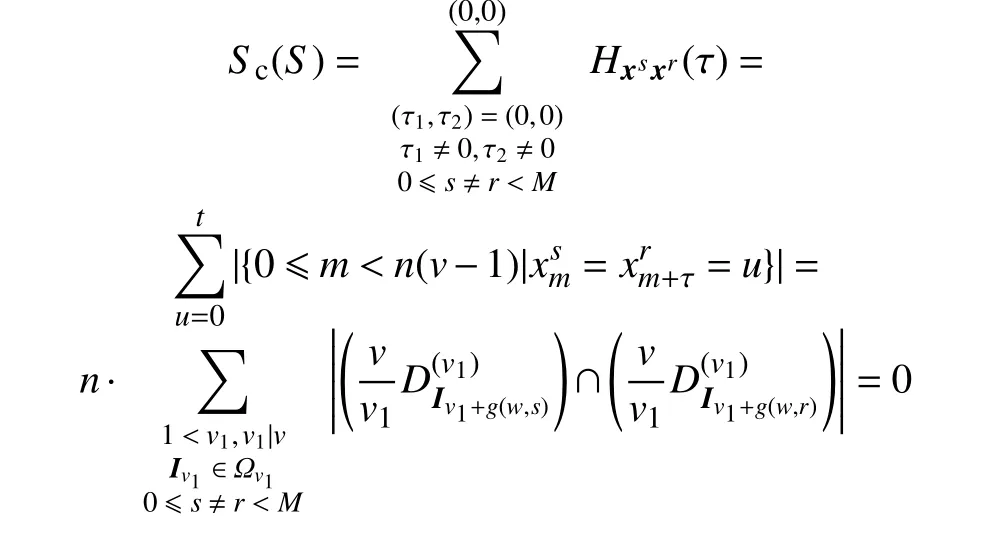
情况2，当τ1≠ 0，τ2=0 时，由g是二元单射,得到

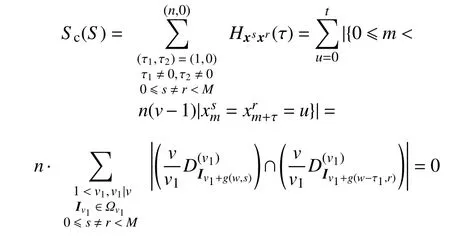
情况3，当τ1=0，τ2≠ 0 时，由g是二元单射,得到

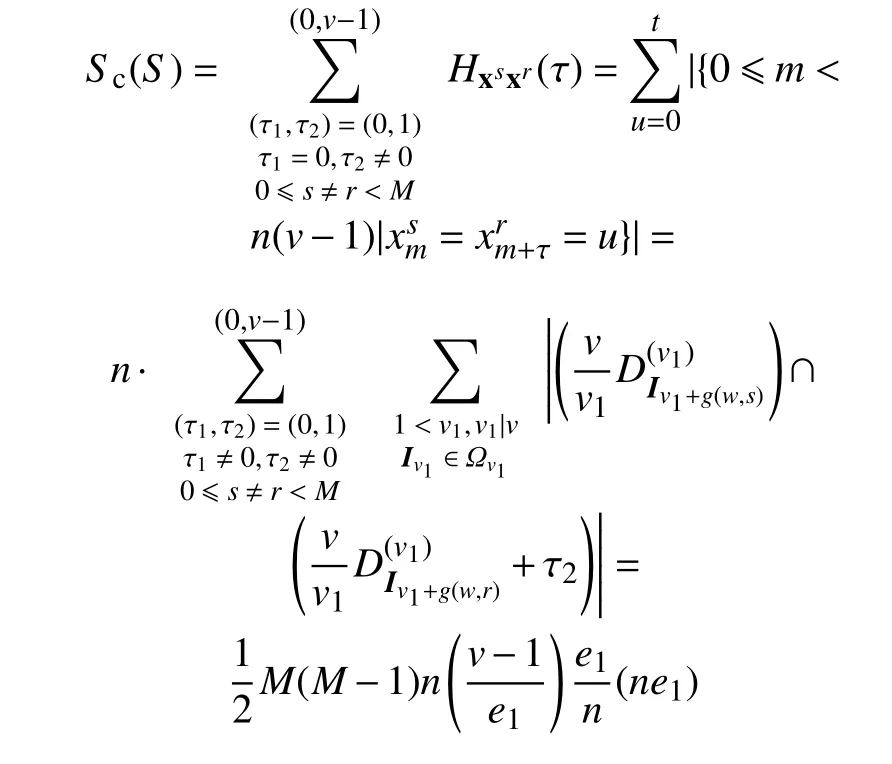
情况4，当τ1≠ 0，τ2≠ 0 时，由g是二元单射，得到

上面讨论的是序列集的汉明互相关总和，即s≠r的情况。当s=r时，在τ1=0，τ2≠ 0 的情况下。其余情况下和互相关结果相同。故综合上面各种情况，可以得到：

2) 根据分圆的性质，汉明自（互）相关的总和是在所有时延下各频点碰撞次数的总和。结合构造得到的跳频序列集频点个数为，由性质1)可得，汉明自相关总和互相关总和分别为：

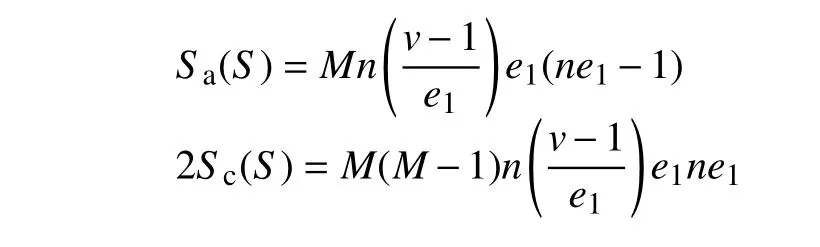
故平均汉明自（互）相关为：

接下来证明跳频序列集S关于平均汉明相关理论界是最优的。

将式(4)、式(5)代入平均汉明相关理论界不等式（3）中，可得

故可得结论

充分发挥诉前程序作用。牢牢把握“诉讼不是目的、维护公益才是目的”的价值目标，将工作的重点放在诉前督促整改环节，督促行政机关履职。通过发出检察建议、约谈、走访、诉前圆桌会议、诉讼风险提示等方式，督促行政机关整改纠错，全面履行法定职责。三年来，全省检察机关共向行政机关发出督促履职检察建议6577件，各地政府职能部门积极整改、主动履职，诉前整改率从2016年的69%上升到目前的93.4%。

构造中结果可使等号成立，故满足理论界要求，因此跳频序列集关于平均相关理论界是最优的。证毕。

例当v=247=13×19 时，v1∈{13，19，247}，e1是12 与18 的公因子，取e1=2 故f1=6，又可知2 是13，19 的公共本原根。

根据构造，可以给出集合A为

x1={107,19,85,38,61,85,105,57,53,61,2,6,116,7,29,76,27,53,122,80,55,40,64,25,94,109,3,26,70,29,60,95,···,95,60,29,70,26,3,109,94,25,64,40,55,80,122,53,27,76,29,7,116,6,2,61,53,57,105,85,61,38,85,19,107}

x2={69,107,47,0,23,47,67,19,15,23,72,76,114,77,99,38,97,15,120,42,35,2,26,95,56,116,73,96,32,99,22,···,22,99,32,96,73,116,56,95,26,2,35,42,120,15,97,38,99,77,114,76,72,23,15,19,67,47,23,0,47,107,69}

x3={31,69,9,88,93,9,29,107,85,93,52,38,112,39,61,0,59,85,118,4,105,72,96,57,18,114,53,58,102,61,92,···，92,61,102,58,53,114,18,57,96,72,105,4,118,85,59,0,61,39,112,38,52,93,85,107,29,9,93,88,9,69,31}

经计算，例构造的长度为492，频点个数为123，序列大小为3 的跳频序列集的平均汉明自相关值和平均汉明互相关值分别是3.006 109 979 63和4，代入平均汉明相关理论界，满足理论界最优。故跳频序列集S是一个满足平均汉明相关理论界最优的跳频序列集。

3 结论

表1 分圆法构造跳频序列集的参数比较