基于切换增益调节的神经滑模控制的机器人位置跟踪
龚双双,刘 霞
(西华大学电气与电子信息学院,四川 成都 610039)
机器人控制容易受到外部干扰等不确定性的影响,所以,设计一种能减小不确定性影响的控制器就尤为重要。滑模变结构控制的滑动模态可以按照需要设计,而且系统的滑模运动与控制对象的参数变化和系统的外界干扰无关;因此,滑模控制相比于其他控制算法具有较高的鲁棒性。但是,滑模控制的不连续开关特性会产生不可避免的抖振现象,即当系统状态轨迹到达滑模面后,难于严格地沿着滑面向着平衡点滑动,而是在滑模面两侧来回穿越,从而产生抖振。抖振会使控制精确度降低,增加能量消耗,严重时会使系统产生振荡或失稳,损坏控制器部件[1-2]。
针对机器人滑模控制抗抖振问题,学者们从不同角度提出了解决方法。文献[3]针对输送用多电机驱动双并联机器人的同步协调问题,提出了一种复合误差鲁棒同步滑模控制方法,与传统的同步滑模控制相比,其鲁棒性更好且滑模控制抖振更小。文献[4]针对风电叶片打磨机器人的力控制问题,采用非奇异快速终端滑模面和多幂次趋近率来设计带扰动补偿的控制律,使机器人的力控制性能更精确,同时减小了滑模控制的抖振。文献[5]针对农用履带机器人轨迹跟踪问题,设计了一种自适应滑模控制,将滑模控制器设计为等效控制和切换控制2 部分,使履带机器人能跟随期望的轨迹运行,同时利用自适应控制方法减小滑模控制的抖振。文献[6]研究了空间三关节机器人的轨迹跟踪问题,采用低通滤波器与滑模控制相结合,解决传统滑模控制中存在的跟踪精度低、抖振较大的问题。文献[7]采用基于遗传算法的积分滑模控制器实现对水下机器人的精准定位和稳定控制,用积分项来定位水下机器人的导航滑模面的误差,缩小了导航定位误差,同时减小了抖振。文献[8]针对机械臂的运动控制问题,提出基于干扰观测器的自适应滑模控制器,该控制器的精确度高,且减小了机械臂的抖振。在这些方法中,滑模控制器内的切换增益都是固定不变的。由于滑模控制的抖振大小与其控制器内的切换增益有关,所以对切换项的增益进行调节,可以达到降低滑模控制抖振的目的。
因此,本文提出了一种基于切换增益调节的神经网络滑模控制方法。该方法在传统滑模控制的基础上结合了神经网络控制方法,利用神经网络逼近滑模控制中切换控制部分的增益,能使切换增益随着机器人关节位置的变化而实时改变。仿真结果表明,与传统的固定增益的滑模控制相比较,该方法能使机器人更好地跟踪期望的位置轨迹,并有效地减轻抖振。
1 机器人的动力学模型
一个n关节机器人,其动力学模型可由二阶非线性微分方程[9]来描述。

2 基于切换增益调节的神经滑模控制
本文采用自适应神经滑模控制器对机器人的位置进行控制。由于滑模控制的抖振大小是由其控制器切换增益K所决定,所以采用RBF 神经网络对切换项的增益K进行调节,以降低滑模控制的抖振。所设计的控制算法的思路如图1 所示。

图1 神经滑模控制系统思路框图
由图1 可以看出,整个控制系统的输入信号为机器人的期望关节角位移r,r减去反馈回来的机器人实际关节角位移q得 到位置的跟踪误差e,然后将e输入给切换面s,得到切换面后,分别设计等效控制器 τde和切换控制器 τqi,切换控制器 τqi中的切换增益K由RBF 神经网络进行调节,接着将等效控制器和切换控制器2 部分相加得到神经滑模控制器τ,将 τ输入给一个有外界干扰 τd的机器人,控制机器人关节的转矩,再接着运用机器人运动学逆解求出机器人的关节角加速度q¨,对q¨求2 次积分得到关节角位移q,再将q反馈给输入信号。
2.1 滑模控制器的设计
机器人轨迹跟踪的控制目标是关节角位移q尽可能好地跟踪期望的关节角位移r。机器人的位置跟踪误差定义为

滑模面[10]定义为

式中,λ为正定对角矩阵,λ=diag(λ1,λ2,λ3,···,λn),其中 λi(i=1,2,3,···,n)均为大于0 的常数。
对式(3)求导,得

将式(2)代入式(4),可得

由式(1)可得

将式(6)代入式(5),可得

滑模控制器的等效控制部分为

式中,τde即为式(7)中的τ(为了和最终的滑模控制器公式(10)区分,故变τ为 τde)。
由于本文研究的对象为不确定的系统,而且具有外界干扰,所以需要再设计一个切换控制器 τqi实现对外界干扰的稳定性控制。切换控制部分为

式中:切换增益K=diag(k1,k2,k3,···,kn),sgn(s)表示符号函数;ki(i=1,2,3,···,n)为大于0 的常数。
由式(8)和(9)可得到滑模控制器,为

控制器 τ由等效控制 τde和切换控制 τqi组成。下面将对 τqi中的切换增益K采用神经网络进行调节。
2.2 切换增益 K 的调节

式中:j=1,2,3,···,m;m为RBF 中隐含层的个数;ρj为隐含层第j个神经元的中心向量;ωj为高斯基函数的长度值。那么,RBF 神经网络的输出为

其中,δj(t)(j=1,2,3,···,m)为RBF 神经网络权值系数。
为了更好地调节切换增益K,对神经网络权值系数δj(t)进行逼近。首先定义一个变量θ,为

网络权值系数 δ(t)=(δ1(t),δ2(t),δ3(t),···,δm(t))按照下列方法进行调节。

式中: μ为网络学习速率;Δδ(t)为网络权值系数的修正项。
将式(13)代入式(14),可得


将式(9)、式(12)代入式(16)整理后,可得

那么,δ(t)的学习算法为

其中,ξ为动量因子,ξ ∈(0,1)。
将式(12)代入原切换控制器式(9),得到新的切换控制器,为

由式(8)和式(19)可知,所设计的基于RBF 神经网络的滑模控制器为

3 仿真研究
为了验证上述神经滑模控制算法的有效性,利用MATLAB 对双关节机器人进行仿真[10],并与传统的滑模控制器进行对比。
双关节机器人的惯性矩阵M(q)为
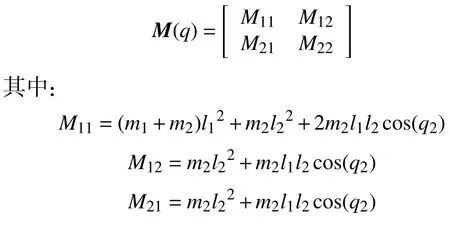

式中:q1、q2为双关节机器人的2 个关节;m1、m2分别为机器人连杆1、连杆2 的质量;l1、l2分别为机器人连杆1、连杆2 的长度。具体数值如表1 所示。

表1 机器人的参数取值
机器人的期望轨迹为

式中: α表示外部干扰的中值;β表示干扰作用的时间范围。仿真中 α=1.5,β=0.09。扰动的大小由φ决定,在仿真中,设置φ=20。
神经元的宽度取为:

网络权值系数初始值取为:

高斯参数取ρ1=10×ones(4,5),ρ2=10×ones(4,5)。
此外,在仿真时,式(14)中 μ=80,式(18)中ξ=0.05。仿真结果如图2、图3、图4 和图5 所示。由图可知:当采用传统滑模控制时,机器人2 个关节的实际位置和期望位置相差较大,最大跟踪误差大约有1.5 rad;当采用基于切换增益调节的神经网络滑模控制时,机器人2 个关节的实际位置能很好地跟踪期望位置,跟踪误差在0.02 rad 以内。

图2 关节1 的位置跟踪
由图6、图7 可知:当采用传统滑模控制时,2 个关节的控制输入会出现较大的抖振现象,尤其是在前2 s 内,抖振较为明显;当采用基于切换增益调节的神经网络滑模控制时,2 个关节的控制输入会随着期望的关节位置的变化而呈周期性的变化,控制输入的抖振更小。
此外,由于传统滑模控制中切换增益是固定的,2 个关节的切换增益将一直保持在[K1K2]T=[ 50 30 ]T不变,故没有给出其增益变化图。由图8 可知,当采用基于切换增益调节的神经网络滑模控制时,2 个关节的切换增益会不断变化,这是由于RBF 神经网络对切换增益的实时逼近,使切换增益会随着关节位置的变化而改变。

图3 关节2 的位置跟踪

图4 关节1 的位置跟踪误差
表2 比较了2 种控制器对机器人关节的位置跟踪误差。由表可知:使用传统滑模控制器控制时,机器人关节1 的位置跟踪误差最大值为1.523 rad,关节2 的最大位置跟踪误差为1.518 rad;使用切换增益调节的神经滑膜控制器控制时,机器人关节1 的位置跟踪误差最大值为0.037 rad,关节2 的最大位置跟踪误差为0.085 rad。

图5 关节2 的位置跟踪误差

图6 关节1 的控制输入
通过对2 种控制器的仿真结果图进行比较发现:传统的滑模控制器对双关节机器人的关节位置跟踪误差较大,抗外部干扰的能力不强,而且控制输入会产生较大的抖振现象;本文设计的基于机器人切换增益调节的神经滑模控制器,对关节的跟踪误差会逐渐收敛到很小的范围内,相比于传统的滑模控制,跟踪误差大大减小,而且有效解决了传统滑模控制方法中抖振较大的问题。

图7 关节2 的控制输入

图8 切换增益的变化

表2 2 种控制器的位置跟踪误差比较
4 结论
本文针对机器人的轨迹跟踪问题,提出了一种基于切换增益的神经滑模控制方法。首先,设计了针对机器人位置的滑模控制器;然后,通过RBF 神经网络来调节滑模控制器中的切换增益,使切换增益能随着外界干扰等不确定项的改变而改变,从而能实时地估计切换增益,解决了传统滑模控制中的抖振问题。通过仿真对比结果表明,与传统的固定增益滑模控制相比,本文提出的方法能有效跟踪机器人的关节位置,大大地减小了跟踪误差。由于本文只在仿真层面对算法进行了验证,今后可以将本文提出的方法在实际的机器人上进行实验,验证算法的有效性。

