基于反向学习与混合位置中心的樽海鞘算法
(成都理工大学信息科学与技术学院,四川 成都 610059)
随着科学的进步,在各领域中所遇到的工程求解优化问题的复杂性越来越高,传统的计算方式难以满足对问题优化的有效性。相关学者通过自然界不同的物理现象、物种进化提出了启发式算法。以粒子群[1]、遗传算法[2]为代表的启发式算法已成功应用于无人艇航线规划[3]、特征选择[4]、图像阈值分割[5]等。
樽海鞘算法(Salp swarm algorithm,SSA)是2017年由Mirjalili 等提出的一 种新型启发式算法[6],其思想来源于樽海鞘链在海洋中觅食的种群机制。与其他优化算法相比,SSA 具有参数少、寻优机制简明等特点,现已成功运用于特征选择[7]、训练神经网络[8]、TDOA 问题[9]、PMSM 多参数辨识[10]等。作为一种随机群体优化算法,它与其他相似算法一样,依旧存在着易陷入局部最优解及收敛速度慢等缺点。已有相关学者对其进行改进,提高算法的性能。文献[11]在樽海鞘算法中引入反向学习与混沌局部搜索,以提高其性能,从而获得全局最优解。文献[12]提出了一种在食物源位置引入疯狂算子的疯狂自适应的樽海鞘算法,并对其优化函数进行了验证。文献[13]将天体运动机制引入到樽海鞘算法,以提高算法的性能。
为提高樽海鞘算法在求解问题时的收敛速度和寻优精度,本文引入不同的优化策略,提出一种基于反向学习与混合位置中心的樽海鞘算法
(opposition-based learning and hybrid position center Salp swarm algorithm,OHSSA)。该算法主要特点体现在以下方面。1)在每次迭代结束后,将领导者更新的位置通过反向学习策略得到领导者的反向解,以增加种群多样性,有利于跳出局部最优。2)构建混合位置中心。通过引入位置加权中心和位置均值中心,引导种群前期能快速地收敛到一个较优的位置,有利于加快算法前期收敛速度。
1 樽海鞘算法
樽海鞘算法是Mirjalil 等[6]根据樽海鞘的群聚行为所提出的群体仿生优化算法。樽海鞘是一种类似于水母的居于深海的生物,主要以浮游植物为食,依靠吸入喷出海水前进。樽海鞘在深海中常常形成一个樽海鞘链的群体,群体分为2 部分:领导者和追随者。樽海鞘链最前端的个体被认为是领导者,其他个体被认为是追随者。领导者根据食物源位置指导引领着跟随者移动。
樽海鞘算法的整个寻优过程起源于樽海鞘链的群聚觅食行为,将樽海鞘群体对最佳食物源搜索的过程类比为对函数寻优。为了更加平衡算法的全局性和鲁棒性,樽海鞘算法选取一半的种群为领导者。在一个N×d维的空间内,N为樽海鞘种群数量,d为空间维度,樽海鞘个体的位置表示为Xn=[Xn1,Xn2,···,Xnd]T,n=1,2,···,N,对应空间维度的食物源表示为F=[F1,F2,···,Fd]T。在SSA 中,领导者的位置更新是根据式(1)进行。
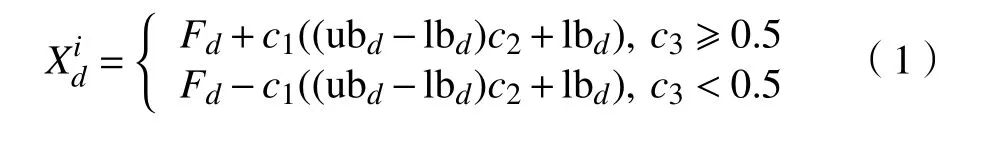
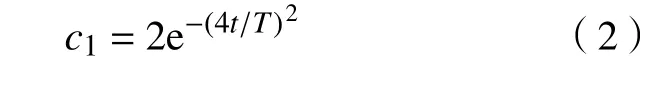
其中,t为当前迭代次数;T为最大迭代次数。追随者的位置更新公式为
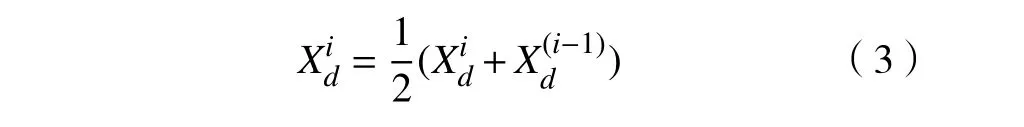
step1,初始化种群,得到每一个樽海鞘的位置。
step2,通过目标函数得到每个樽海鞘位置对应的适应度值。
step3,对所有的适应度值进行排序,将最佳的适应度值作为食物源。
step4,选取前一半的樽海鞘个体为领导者,其余个体为追随者。
step5,根据式(1)更新领导者位置。
step6,根据式(3)更新追随者位置。
step7,将全局最佳樽海鞘位置作为新的食物源。
step8,判断是否达到最大迭代次数:若是,则结束迭代,输出最佳食物源位置;否则返回step4 继续迭代。
2 基于反向学习与混合位置中心的樽海鞘算法
2.1 反向学习策略
2005 年Tizhoosh[14]提出一种反向学习策略,其原理为对目标空间一个已知解,通过反向学习策略得到其在空间的反向解,以提高种群多样性,选取更优的解作为当前解,能有效地克服算法陷入局部最优解。
定义1反向点。在d维搜索空间[lb,ub]中,x∈[lb,ub],是实数。x的反向解用x′表示,则x′采用式(4)求解。
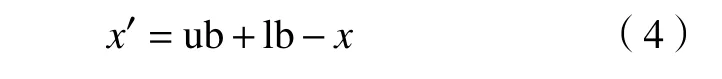
定义2 动态反向学习。假设X=[X1,X2,···,Xn],n=1,2,···,N。经过反向学习后的位置X′=[,,···,],n=1,2,···,N。X′通过式(5)求解。
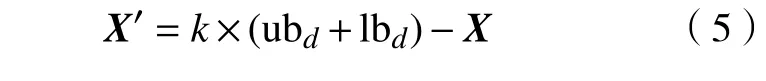
式中:k=rand(·);ubd=max(X);lbd=min(X)。
改进的樽海鞘算法将领导者位置作为反向学习个体,通过领导者在目标空间中的反向解来增加种群的多样性。本文采用定义2 对每次迭代后的领导者位置Xi(i=1,2,···,N/2)进行反向学习,生成反向领导者位置(i=1,2,···,N/2),然后对比适应度函数值,若F() 优于F(Xi),则Xi=。
2.2 混合位置中心
在SSA 中,食物源位置的优劣直接影响着整个樽海鞘链对食物的搜寻结果。文献[15]通过适应度值在人工蜂群算法中构建了一个加权中心值,加快了算法的收敛速度。为此,在SSA 中,引入混合位置中心,在算法的前期,通过引入不同的位置中心,使SSA 快速地收敛到最优食物源位置附近,以加快SSA 的收敛速度。
2.2.1 位置加权中心
SSA 在进行迭代更新时,在搜索域中的每一个位置对应一个食物源,故根据所有的食物源构建位置加权中心。位置加权中心构建过程如下。
SSA 在每次迭代更新前,对上一次迭代所获得的N个食物源位置进行排序,将每个位置的排序值作为自身的位置加权权重值,如排序第一的食物源位置,加权权重为N,以此类推,最后一个食物源位置的加权权重值为1。位置加权中心为
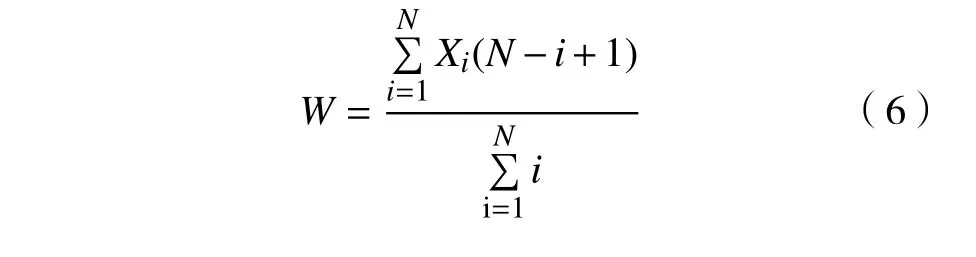
式中:N为种群数量;Xi为食物源位置排序中第i个位置;N-i+1为Xi的位置加权权重值。
2.2.2 均值中心
种群随机初始化在搜索域中每个位置都对应其适应度值,最佳适应度值为当前全局的一个峰值,越靠近峰值的个体所得到的适应度值越优。中心极限定理[16]指出,大量独立随机变量的均值近似于正态分布。在正态分布N(μ,σ2)中,均值位置对应当前分布的峰值。SSA 的个体初始化位置近似于正态分布,通过个体迭代收敛于全局峰值,则在算法中所有个体位置的均值应与正态分布μ重合,故均值中心构建为

故混合位置中心值将两者位置中心的优势结合,表示为

在引入混合位置后,通过目标函数判断混合位置中心与食物源位置的优劣,并将最优的位置作为新的食物源位置。
2.3 OHSSA 的伪代码
1)设置OHSSA 参数:最大迭代次数T,种群数量大小N,两须距离d0等。
2)随机初始化种群,计算每个樽海鞘位置的适应度值,通过排序将最佳的适应度值对应的位置作为食物源位置Xbest。
3) While(t<T)
4)根据式(8)得到混合位置中心值。
5) For(i=1:N)
6) if (i<N/2)
7)根据式(1)更新领导者位置。
8) else
9)根据式(3)更新追随者位置。
10) end if
11) end for
12)计算种群个体的适应度值并更新食物源位置。
13)将食物源位置通过式(5)进行反向学习,得到反向食物源位置。
14)判断反向食物源位置与食物源位置优劣,并更新食物源位置。
15)t=t+1。
16) end while。
17)返回最佳食物源位置Xbest及其适应度值。
3 仿真实验与结果分析
为验证本文提出的OHSSA 的有效性和鲁棒性,在8 个包含单峰、多峰、可分、不可分等不同特征的测试函数上,如表1 所示,对OHSSA 与引入领导者反向学习的樽海鞘算法(OSSA)、引入混合位置中心的樽海鞘算法(HSSA)、标准樽海鞘算法(SSA)、标准粒子群算法(PSO)进行测试。对每个算法设置相同的条件,最大迭代次数为1 000,种群数为30,在MATLAB14b 上采用M 语言实验,统计每个算法独立运行50 次的最佳适应度值Fbest、平均最佳适应度值Mean、最佳适应度值标准差Std 及平均运行时间。实验测试结果如表2 所示。
表2 的50 次实验运行结果表明:在所有测试函数中,OHSSA 都具有最佳的实验结果;在f2函数中,所有樽海鞘算法的平均收敛精度、标准差都在一个级别上,与PSO 相比,所有樽海鞘算法在各个结果上都具有一定优势;在f5函数中,所有算法都达到了理论最优值,所有樽海鞘算法的标准差比PSO 要小得多,说明樽海鞘算法的稳定性更好;在其他测试函数中,只引入一种改进方式的OSSA、HSSA 相比于标准的SSA,在寻优结果、平均值以及标准差上均有所提高,说明改进的SSA 比标准的SSA 具有更佳的可行性和鲁棒性;SSA 与PSO 在同一测试函数中的实验结果对比表明,SSA 具有更高的收敛精度和稳定性;改进的SSA 在平均寻优时间上都长于基本SSA,这是由于改进算法对个体适应度值进行排序延长了算法的运行时间。
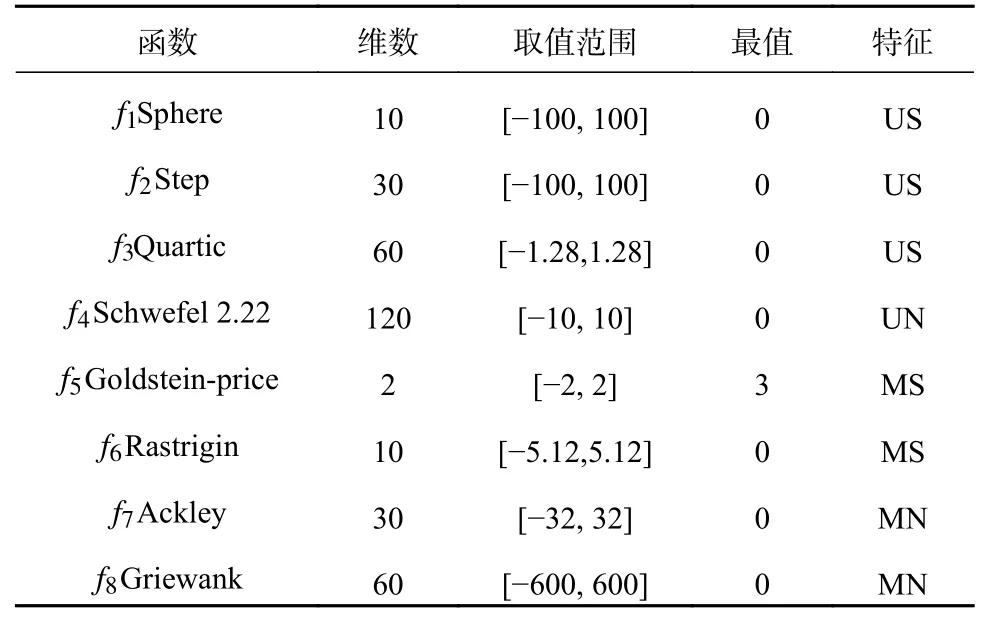
表1 测试函数
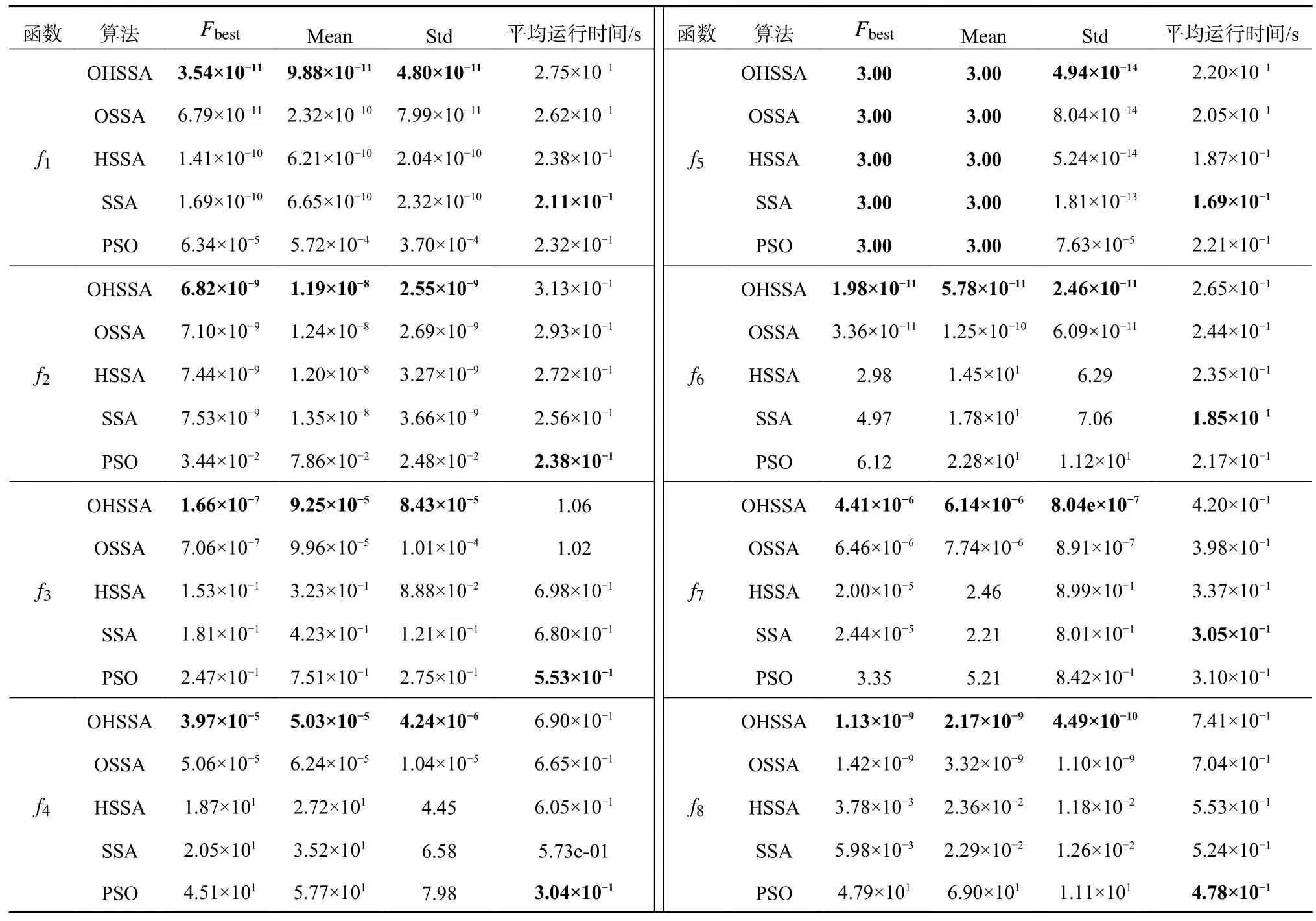
表2 测试结果
图1 示出各算法对不同函数优化的收敛曲线。由图可以看出:在单峰测试函数(f1-f4)中,相比于没有引入混合位置中心的SSA、OSSA,OHSSA 和HSSA 在种群迭代前期的收敛速度更快,更接近于最佳适应度值,表明通过引入混合位置中心,能够加快算法的收敛速度,在寻优精度上,引入领导者反向学习的OHSSA 和OSSA 具有更高的寻优精度,随着空间维数的不断增加,所有算法寻优精度均不断减少,但OHSSA 算法的寻优精度依旧相比于其他算法是最高的;在多峰测试函数(f5-f8)中,f5函数中各算法的收敛速度和收敛精度基本一致;在除f5外的其他多峰测试函数中,各算法在相同维度的情况下,受寻优函数多个不同的局部最优解影响,寻优精度比单峰测试函数要低,但在多峰低维函数中,所有算法都能达到理论最优值,面对多峰高维的情况,OHSSA 的寻优精度都高于其他算法,只引入了一个影响因子的HSSA和OSSA 的寻优精度均高于SSA。
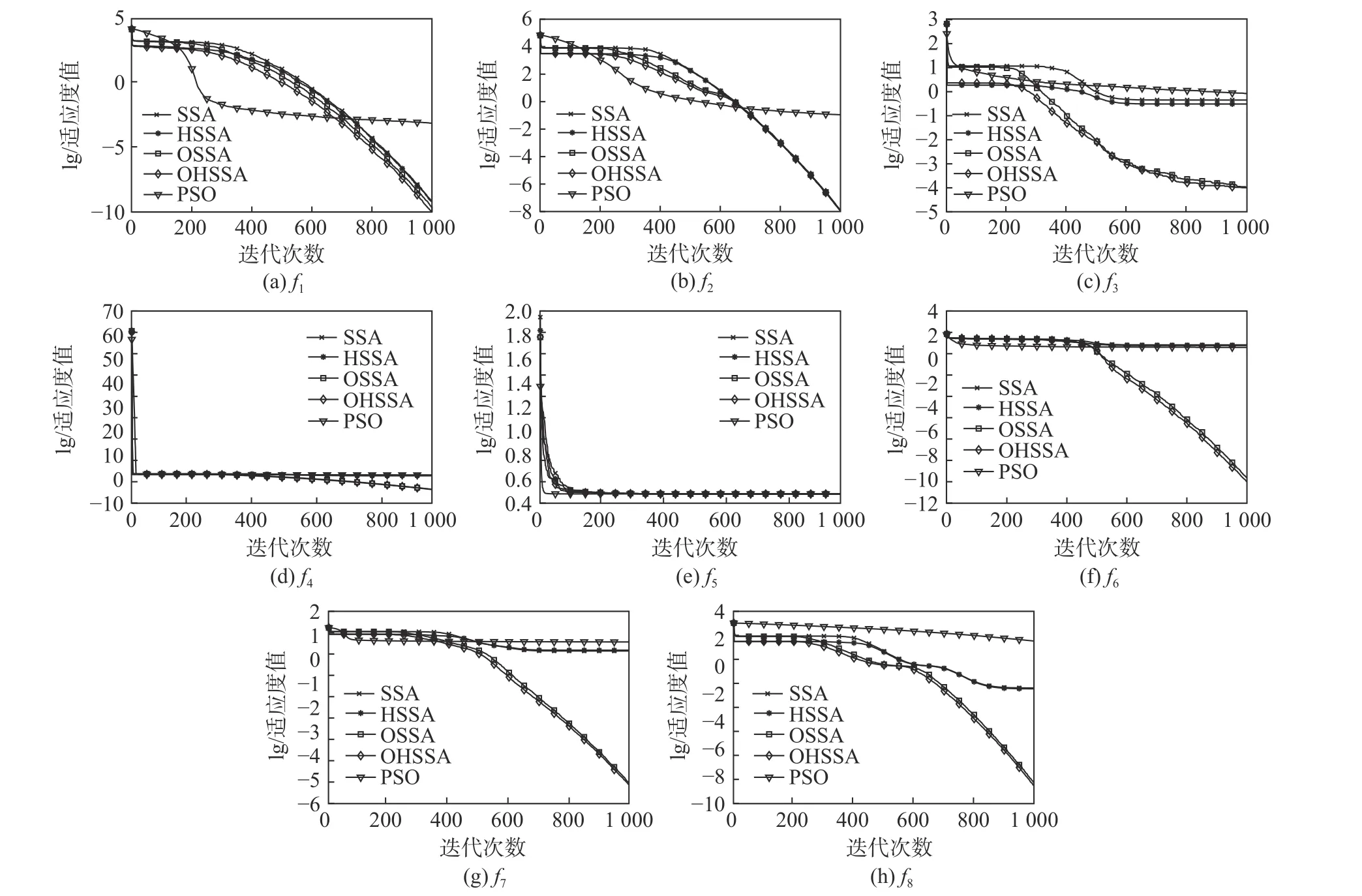
图1 各算法的收敛曲线
4 结论
本文通过引入混合位置中心和对领导者位置进行反向学习,提出一种基于反向学习和混合位置中心的樽海鞘算法。引入混合位置中心,在迭代前期可以加快算法的收敛速度,使算法能够快速地收敛到一个较优的位置;对领导者位置进行反向学习,有利于跳出局部最优解,提高算法的收敛精度。对改进的樽海鞘算法通过不同的基准函数测试,其实验结果表明:改进的樽海鞘算法具有更快的收敛速度,能够收敛到精度更高的最优解,在可行性及鲁棒性方面都更具有优势。在下一步研究中,笔者尝试将改进的算法应用到具体的工程中。

