低碰撞区跳频序列平均部分汉明相关理论界研究
牛宪华1,曾柏森
(1.西华大学数学与计算机学院, 四川 成都 610039;2. 中国联通成都市分公司网络优化中心, 四川 成都 610036)
跳频(frequency-hopping, FH)多址扩频系统具有抗干扰、抗截获、安全和多址接入的性能,并能与频谱资源共享,在军事无线电通信、移动通信、现代雷达和声纳回声定位系统中有广泛应用[1-3]。对于跳频通信系统,通常要求发射机之间的相互干扰(mutual interference ,MI)尽可能地保持在低水平。当多个发射机在同一时刻使用相同的频率发射信号时,就会产生相互干扰,而跳频通信系统相互干扰的大小严重依赖于跳频序列的汉明相关性;因此,为准确分析跳频通信系统的性能,必须仔细研究跳频序列的汉明相关特性。跳频序列集的汉明相关值与频隙个数、序列长度、序列个数等参数有关,这些参数受理论界的限制。跳频序列理论界是跳频序列集性能优异的评价标准,对跳频序列设计具有重要的指导意义。
由于跳频系统中同步时间的有限性以及硬件的复杂性,通常跳频序列相关窗的长度小于所选序列的周期,而且相关窗的长度会随着信道条件的变化而变化;所以部分汉明相关比全周期汉明相关能更好地衡量系统的性能[4]。
对于异步跳频通信系统,希望每个跳频序列在整个周期内没有碰撞,但是由跳频序列集汉明相关函数的理论界可知,满足条件的跳频序列的数目非常少,不能满足较多用户的使用。如果将跳频序列的汉明相关值限制在零时延附近的一个小的时延范围内,就能构造出较多汉明相关性能好、序列长度长的跳频序列。这正是低碰撞区跳频序列的基本思想[5]。为方便区分,本文将考虑全部时延的跳频序列称为常规跳频序列,把考虑低碰撞区的跳频序列称为低碰撞区跳频序列。本文主要研究低碰撞区跳频序列集的平均周期部分汉明相关理论界。
1 定义和理论界
设F={f1,f2, …,fq}是一个大小为q的频点集,S是由F上M个长度为N的跳频序列组成的集合。对于任意的f1,f2∈F,令
对于S中任意2个跳频序列x=(x0,x1,…,xN1),y=(y0,y1,…,yN1)∈S,x和y在相对时延为τ时的周期汉明相关函数Hxy(τ)定义为

(1)
其中,下标j+τ按模N运算,并且只考虑正时延。
对于一个跳频序列集S,序列集的最大周期汉明自相关Ha(S)和最大周期汉明互相关Hc(S)分别定义为:
(2)
为简化和方便,令Ha=Ha(S),Hc=Hc(S)。
早在1974年,A. Lempel 等[3]建立了单个跳频序列最大周期汉明自相关的理论界。
引理1(Lempel-Greenberger界) 令F是一个大小为q的频隙集,对于一个F上长度为N的跳频序列x,有
(3)
其中,r是N模q的最小非负剩余。
2004年,D.Y.Peng等[6]推导了跳频序列集最大周期汉明相关的理论界。
引理2(Peng-Fan 界) 令F是一个大小为q的频隙集,S为F上M个长度为N的跳频序列构成的集合,有:
(N-1)qHa+(M-1)NqHc≥(NM-q)N
(4)
(N-1)MHa+(M-1)NMHc≥2INM-(I+1)Iq
(5)
其中,I=⎣NM/q」。
可以看出,当M=1时,Lempel-Greenberger界是Peng-Fan界的特殊情况。如果跳频序列集的相关性满足Peng-Fan界取等号,称这个跳频序列集为最优跳频序列集。现有序列构造结果中,有很多跳频序列集[7-10]满足Peng-Fan界。
平均汉明相关是衡量跳频序列集的另一个重要参数。对于任意跳频序列集S,序列集的平均周期汉明自相关Aa(S)和平均周期汉明互相关Ac(S)分别定义为:
(6)
(7)
为简化和方便,令Aa=Aa(S),Ac=Ac(S)。
2008年,D.Y.Peng等[11]推导了跳频序列集平均周期汉明相关的理论界。
引理3(Peng-Peng-Tang-Niu 界) 令F是一个大小为q的频隙集,S为F上M个长度为N的跳频序列构成的集合,有
q(N-1)Aa+qN(M-1)Ac≥(NM-q)N
(8)
Peng-Peng-Tang-Niu 界首次考虑了跳频序列的平均汉明相关性质。如果跳频序列集的平均汉明相关性满足Peng-Peng-Tang-Niu界取等号,称这个跳频序列集关于平均汉明相关的理论界是最优的。
对于任意2个跳频序列x=(x0,x1,…,xN1),y=(y0,y1,…,yN1)∈S,x和y在相对时延为τ、相关窗起点为j、长度为L时的部分汉明相关函数定义为
(9)
当x=y时,Hxy(j|L;τ)称为部分汉明自相关函数;当x≠y时,则称为部分汉明互相关函数。如果j=0 并且L=N,式(9)表示式(1)中定义的周期汉明相关函数。
对于跳频序列集S,序列集的最大部分汉明自相关Pa(L)和最大部分汉明互相关Pc(L)分别定义为:
为简化和方便,在不引起混淆的情况下,令Pa=Pa(L),Pc=Pc(L)。
2004年,Y.C. Eun等[4]给出了跳频序列最大周期部分汉明自相关的理论界。
引理4(Eun-Jin-Hong-Song界) 令F是一个大小为Q的频隙集, 对于F上长度为N,相关窗长度为L的跳频序列,有
(10)
其中,r是N模q的最小非负剩余。
可以看出,当L=N时,Lempel-Greenberger界是Eun-Jin-Hong-Song界的特殊情况。对于给定的相关窗长度L(1≤L≤N),如果序列集S的最大周期部分汉明相关函数满足Eun-Jin-Hong-Song界取等号成立,那么就称跳频序列集S关于最大周期部分汉明相关函数的理论界是最优的。目前已经构造出几类关于Eun-Jin-Hong-Song界最优的跳频序列集[4,12]。
低碰撞区跳频序列是低相关区扩频序列在跳频通信系统中的推广。低碰撞区跳频序列作为一个新的研究方向,近年来引起国内外学者的兴趣。
对于任意跳频序列集S,令整数HLa≥0,HLc≥0,跳频序列集S的周期汉明相关低碰撞区LHZ、周期汉明自相关低碰撞区LAHZ和周期汉明互相关低碰撞区LCHZ分别定义为:
LHZ=min{LAHZ,LCHZ}
LAHZ=max{T|Hxx(τ)≤HLa,for0<τ≤T,∀x∈S}
LCHZ=max{T|Hxy(τ)≤HLc,for0≤τ≤T,∀x,y∈S,x≠y}
当HLa=HLc=0时,S的低碰撞区称为S的无碰撞区NHZ。一个具有LHZ≥0或NHZ≥0的跳频序列集S称为关于周期汉明相关的低碰撞区跳频序列集或无碰撞区跳频序列集。
2006年,D.Y.Peng等[13]推导了低碰撞区跳频序列集周期汉明相关的理论界。
引理5(Peng-Fan-Lee 界) 令F是一个大小为q的频隙集,S为F上M个长度为N的跳频序列构成的集合,LHZ是序列集S关于周期汉明相关函数的低碰撞区。对于任意整数Z,0≤Z≤LHZ,有
qZHa+q(M-1)(Z+1)Hc≥(Z+1)NM-Nq
(11)
NMZHa+NM(M-1)(Z+1)Hc≥(Z+1)[(2I+1)NM-(I+1)Iq]-N2M
(12)
其中,I=⎣NM/q」。
跳频序列的Peng-Fan 界和Lempel-Greenberger界都是Peng-Fan-Lee 界的特殊情况。关于Peng-Fan-Lee界最优的低碰撞区跳频序列集近年来也有许多构造结果[14-17]。
考虑低碰撞区跳频序列集的周期部分汉明相关性质,可以得到如下定义。
令F是一个大小为q的频隙集,S为F上M个长度为N的跳频序列构成的集合,对于任意给定相关窗L(L≤N),令正整数PLa(L)≥0,PLc(L)≥0,那么跳频序列集S的周期部分汉明相关低碰撞区LPHZ(L)、周期部分汉明自相关低碰撞区LPAHZ(L)和周期部分汉明互相关低碰撞区LPCHZ(L)分别定义为:
for0<τ≤T,0≤j for0≤τ≤T,0≤j 特别地,当j=0且L=N时,序列集S的周期部分汉明相关低碰撞区、周期部分汉明自相关低碰撞区和周期部分汉明互相关低碰撞区分别是上面定义的跳频序列集的周期汉明相关低碰撞区、周期汉明自相关低碰撞区和周期汉明互相关低碰撞区。 为简便,在不引起混淆的情况下,令PLa=PLa(L),PLc=PLc(L),LPHZ=LPHZ(L)。 2009年,作者[18]推导了低碰撞区跳频序列集最大周期部分汉明相关理论界。 引理6(Niu-Peng-Liu界) 令F是一个大小为q的频隙集,S为F上M个长度为N的跳频序列构成的集合,相关窗长度为L(L≤N),LPHZ为跳频序列集S的周期部分汉明相关低碰撞区,那么对于任意正整数Z,0≤Z≤LPHZ,有: qZPLa+q(M-1)(Z+1)PLc≥(Z+1)LM-Lq (13) MNZPLa+M(M-1)N(Z+1)PLc≥(Z+1)L[(2I+1)M-I(I+1)q/N]-LMN (14) 其中,I=⎣NM/q」。 现有的Lempel-Greenberger界、Peng-Fan 界、Peng-Fan-Lee 界和Eun-Jin-Hong-Song界都是Niu-Peng-Liu界的特殊情况。Niu-Peng-Liu界是跳频序列集关于最大周期汉明相关和最大周期部分汉明相关的现阶段最完整的理论界,而对于跳频序列集平均汉明相关性质的理论界,现阶段只有Peng-Peng-Tang-Niu界考虑了常规跳频序列集的平均周期汉明相关;因此,本文将主要考虑低碰撞区跳频序列集的平均部分汉明相关,构造低碰撞区跳频序列集平均部分汉明相关的理论界。 首先给出低碰撞区跳频序列集平均周期部分汉明相关的定义。 定义1令F是一个大小为q的频隙集,S是F上由M个长度为N的跳频序列组成的集合,相关窗长度为L(L≤N),LPHZ为跳频序列集S的周期部分汉明相关低碰撞区,那么对于任意正整数Z,0≤Z≤LPHZ,将: (15) (16) 分别称为低碰撞区跳频序列集S的周期部分汉明自相关总碰撞次数和周期部分汉明互相关总碰撞次数。跳频序列集S在低碰撞区的平均周期部分汉明自相关和平均周期部分汉明互相关可表示为: (17) (18) 下面给出本文的重要定理,即低碰撞区跳频序列集平均周期部分汉明自相关和平均周期部分汉明互相关理论界。 定理1令F是一个大小为q的频隙集,S为F上M个长度为N的跳频序列构成的集合,相关窗长度为L(L≤N),LPHZ为跳频序列集S的周期部分汉明相关低碰撞区,那么对于任意正整数Z,0≤Z≤LPHZ,有: (19) (20) 其中,I=⎣NM/q」。 证明:对于任意正整数Z,0≤Z≤LPHZ,有 NM+(1/L)Sa+(2/L)Sc≥(Z+1)NM2/q NM+(1/L)Sa+(2/L)Sc≥(Z+1)[(2I+1)M-I(I+1)q/N] 其中,I=⎣NM/q」。那么,基于低碰撞区跳频序列集平均周期部分汉明相关的定义,有: 证毕。 在定理1中,令j=0,L=N,则跳频序列集S的周期部分汉明相关低碰撞区LPHZ即为序列集S的周期汉明相关低碰撞区LHZ,由此可以得到低碰撞区跳频序列集平均周期汉明相关函数的理论界。 推论1令F是一个大小为q的频隙集,S为F上M个长度为N的跳频序列构成的集合,相关窗长度为L(L≤N),LHZ为跳频序列集S的周期汉明相关低碰撞区,那么对于任意正整数Z,0≤Z≤LHZ,有: (21) (22) 其中,I=⎣NM/q」。 定理1和推理1给出了低碰撞区跳频序列集平均周期部分汉明相关和平均周期汉明相关的理论界。理论界的提出对设计具有优异平均周期部分汉明相关和平均周期汉明相关的低碰撞区跳频序列有很好的指导意义。 例1令q=7,N=7,M=6,L=7,LPHZ=6,代入定理1中可得 令频隙集F={0, 1, 2, 3, 4, 5, 6}, 可构造跳频序列集S={S0,S1,S2,S3,S4,S5}, 其中,S0=0116166,S1=0225255,S2=0334344,S3=0443433,S4=0552522,S5=0661611。序列集的部分汉明相关值为 本文构造了低碰撞区跳频序列平均部分汉明相关的理论界,通过理论界给出了跳频序列集序列长度、序列个数、频隙个数、平均周期部分汉明自相关和平均周期部分汉明互相关所满足的理论约束关系。已有理论界都可以看作是本文理论界的特殊情况,新理论界的提出对于跳频序列的设计和评估有很好的指导意义。 [1] Fan P Z, Darnell M. Sequence Design for Communications Applications[M]. London: RSP John Wiley & Sons Inc, 1996:271-350. [2] Golomb S W, Gong G. Signal Design for Good Correlation: for Wireless Communication, Cryptography and Radar[M]UK: Cambridage Univ Press,2005:402-417. [3] Lempel A , Greenberger H. Families of Sequence with Optimal Hamming Correlation Properties[J].IEEE Trans Inf Theory,1974, 20:90-94. [4] Eun Y C , Jin S Y , Hong Y P , et al. Frequency Hopping Sequences with Optimal Partial Autocorrelation Properties[J].IEEE Trans Inf Theory, 2004, 50:2438-2442. [5] Wang X N, Fan P Z. A Class of Frequency Hopping Sequences with no Hit Zone[C]// Proceeding of the 4th International Conference on Parallel and Distributed Computing, Applications and Technologies. Chengdu, China:IEEE Press, 2003: 896-898. [6] Peng D Y , Fan P Z. Lower Bounds on the Hamming Auto-and Cross Correlations of Frequency Hopping Sequences[J].IEEE Trans Inf Theory, 2004,50:2149-2154. [7] Ding C, Fuji-Hara R, Fujiwara Y, et al. Sets of Frequency Hopping Sequences: Bounds and Optimal Constructions[J] .IEEE Trans Inf Theory,2009,55:3297-3304. [8] Ge G N, Miao Y, Yao Z X. Optimal Frequency Hopping Sequences: Auto-and Cross-correlation Properties[J]. IEEE Trans Inf Theory,2009, 55: 867-879. [9] Chung J H, Yang K. New Frequency-hopping Sequence Sets with Optimal Average and Good Maximum Hamming Correlations[J].IET Communications,2012,6:2048-2053. [10] Zeng X Y, Cai H, Tang X H, et al. A Class of Optimal Frequency Hopping Sequences with New Parameters[J].IEEE Trans Inf Theory,2012,58 :4899-4907. [11] Peng D Y , Peng T , Tang X H , et al. A Class of Optimal Frequency Hopping Sequences Based on the Theory of Power Residues[J]. Proceeding of the 5thInternational Conference on Sequences and their Applications Lexington, 2008,5203:188-196. [12]Niu X H , Peng D Y , Zhou Z C. Frequency/time Hopping Sequence Sets with Optimal Partial Hamming Correlation Properties[J]. Science China,2012,55(10):2207-2215. [13] Peng D Y , Fan P Z , Lee M H. Lower Bounds on the Periodic Hamming Correlations of Frequency Hopping Sequences with Low Hit Zone[J]. Science in China: Series F Information Sciences,2006, 49(2):1-11. [14] Ma W P, Sun S H. New Designs of Frequency Hopping Sequences with Low Hit Zone[J]. Designs, Codes and Cryptography,2010, 60:145-153. [15] Niu X H, Peng D Y, Zhou Z C. New Classes of Optimal Low Hit Zone Frequency Hopping Sequences with New Parameters by Interleaving Technique[J]. IEICE Transactions on Fundamentals,2012, 95:1835-1842. [16] Niu X H, Peng D Y, Zhou Z C. New Classes of Optimal Frequency Hopping Sequence Sets with Low Hit Zone[J]. Advances in Mathematics of Communications,2013, 7 :293-310. [17] Chung J H, Yang K. New Classes of Optimal Low-hit-zone Frequency-hopping Sequence Sets by Cartesian Product[J]. IEEE Trans Inf Theory, 2013, 59: 726-732. [18] Niu X H , Peng D Y, Liu F. Lower Bounds on the Periodic Partial Correlations of Frequency Hopping Sequences with Partial Low Hit Zone[C]//The Fourth International Workshop on Signal Design and Its Applications in Communications (IWSDA’2009). Fukuoka, Japan:[s.n.], 2009: 84-87.2 低碰撞区跳频序列平均周期部分汉明相关理论界

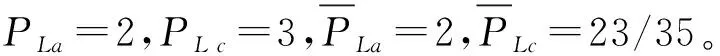
3 结束语


