广义变系数Kadomtsev-Petviashvili方程的孤子解
郭婷婷
(山西工程科技职业大学,山西 太原030619)
0 引言
在许多工程领域中,非线性偏微分方程用以描述自然界中的非线性现象.与经典的常系数孤子方程相比,变系数孤子方程更能贴近现实地反映问题的本质,因此,对广义变系数非线性方程的研究受到广大研究学者的关注.
对于常系数的(2+1)维Kadomtsev-Petviashvili方程[1]

专家们曾对其做了一系列的研究工作,可以采用对称与微分方程约化法[2]来构造该方程的孤子解,这一方法主要基于Lie群[3]及Lie代数结构[4],但计算量偏大.1998年,范恩贵等人将齐次平衡法作改进,给出新的方程约化法[5]来求此类非线性方程的解[6].对于孤子方程求解的方法,瑞典几何学家Bäcklund给出了Bäcklund变换法,Darboux提出Darboux变换法,Gardner、Greene、Kruskal和Miura求解Schrödinger方程N孤子解时给出了反散射法,20世纪以来,Hirota提出了双线性方法等.
本文主要来研究广义变系数Kadomtsev-Petviashvili方程
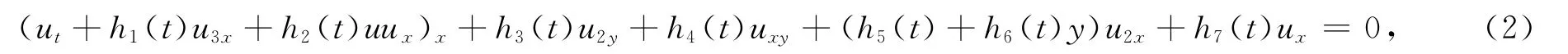
这里u(x,y,t)是关于时间变量t和空间变量x和y的函数,hi(t)(i=1,2,…,7)是关于时间变量t的实函数.针对高维孤子方程,范恩贵等人曾通过引入双线性变换[7],给出方程的双线性形式,并得到孤子方程的多孤子解.基于双线性方法,曾构造出孤子方程的双线性Bäcklund变换[8],Lax对和无穷守恒律[9],进而运用双Bell多项式方法对方程的可积性[10]进行了研究.本文将借助多元变换技巧,将广义变系数Kadomtsev-Petviashvili方程(2)约化为常系数的(2+1)维Kadomtsev-Petviashvili方程(1),并对方程(1)的解作逆映射来构造广义变系数Kadomtsev-Petviashvili方程(2)的孤子解.
1 多元变换技巧
将广义变系数Kadomtsev-Petviashvili方程(2)约化为经典的(2+1)维Kadomtsev-Petviashvili方程(1),首先引入多元变换

这里,

其中,H(t)≠0,B(t)≠0,D(t)≠0,E(t)≠0,A(t),G(t),T(t)为待定系数,将变换(3)和(4)代入方程(2),经整理有以下的关系式成立
为将方程(5)约化为经典的(2+1)维Kadomtsev-Petviashvili方程(1),则需满足以下的关系式
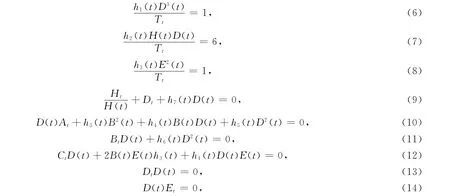
联立求解关系式(6)-(14),得:

这里,c1,c2,c3,c4,c5,c6,c7为积分常数,且c1≠0,c2≠0,c3≠0.将关系式(15)-(21)代入多元变换(3)和(4),便可将广义变系数孤子方程(2)约化为常系数孤子方程(1),这将为方程(2)的求解奠定基础.
2 广义变系数Kadomtsev-Petviashvili方程的孤子解
在双线性方法中,通过对非线性孤子方程作对数变换,可以将(2+1)维Kadomtsev-Petviashvili方程(1)双线性化,通过使用Wronskian技巧,得出(2+1)维Kadomtsev-Petviashvili方程(1)的单孤子解、双孤子解等.在此基础上,结合多元变换(3)和(4),构造广义变系数Kadomtsev-Petviashvili方程(2)的单孤子解

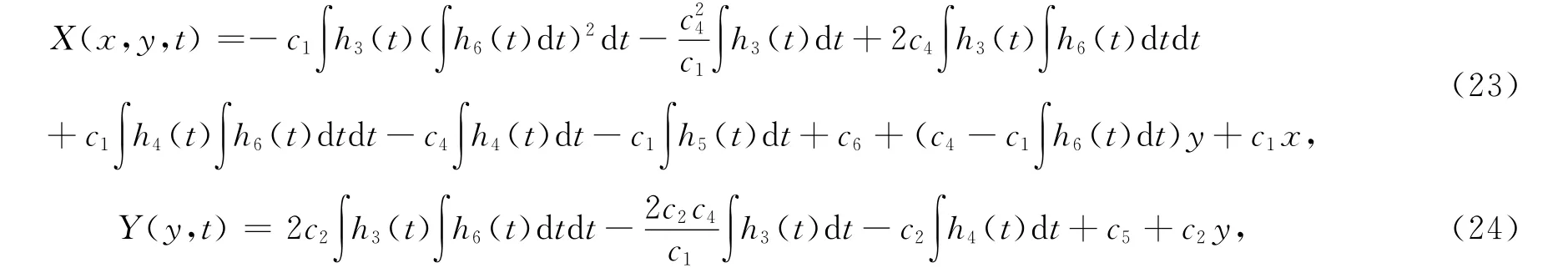
T(t)和H(t)分别满足关系式(20)和(21),这里,为任意常数,h3(t),h4(t),h5(t),h6(t),h7(t)为任意关于变量t的函数关系式.将单孤子解(22)中的参数做如下的赋值,

并取h3(t)=h4(t)=h5(t)=h6(t)=h7(t)=t,当t分别取1.5和2时,描绘出波动三维图像,见图1.

图1 参数t=1.5(a)和t=2(b)时单孤子解(22)的三维图
结合图1分析,该孤波是单孤波,并且随着时间的推移,孤波由y轴的正半轴向负半轴方向进行传播.
广义变系数Kadomtsev-Petviashvili方程(2)的双孤子解为

其中


并将关于t的函数h3(t),h4(t),h5(t),h6(t),h7(t)全设为t,现分别将t取为1.9和2.3,绘制这两个时刻的波形图及二维平面的密度图,见图2和图3.
结合图2、图3中的三维图以及二维密度图分析,随着时间的推移,两列孤波分别沿着y轴的正、负两个方向延展性地传播.
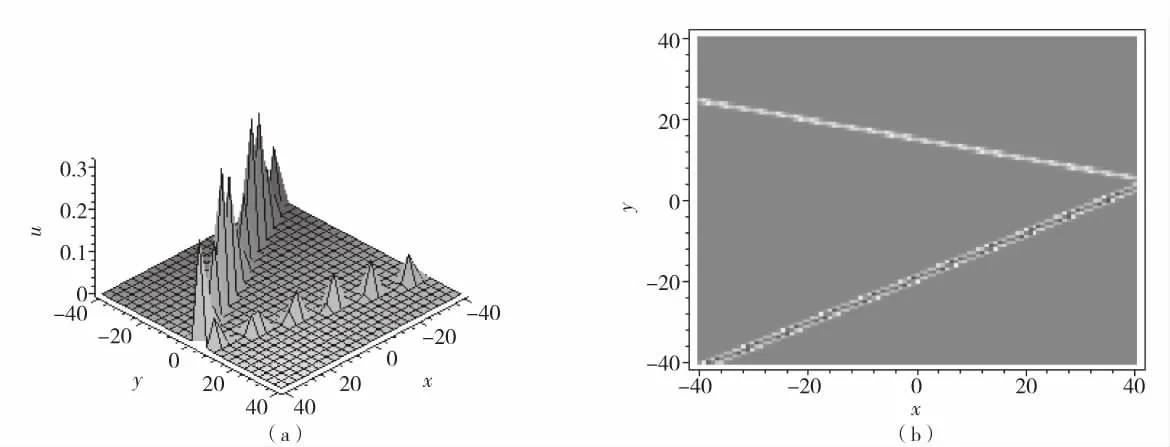
图2 参数t=1.9时双孤子解(25)的三维图(a)和灰度图(b)

图3 参数t=2.3时双孤子解(25)的三维图(a)和灰度图(b)
将以上变系数孤子方程(2)的单孤子解(22)、双孤子解(25)进行推广,通过归纳可以得出广义变系数Kadomtsev-Petviashvili方程(2)的N孤子解
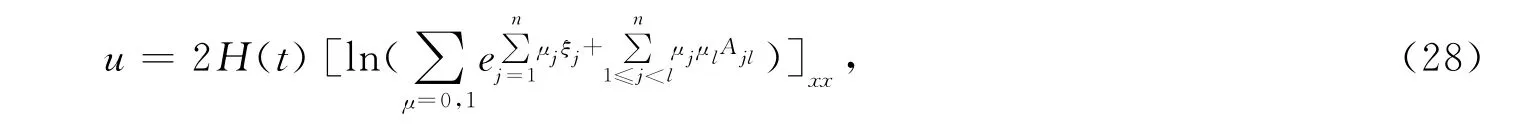
其中,

这里,对μ求和是取μj为0或1的所有可能组合,X(x,y,t),Y(y,t)满足关系式(23)、(24),T(t),H(t)满足关系式(20)、(21),为任意常数,h3(t),h4(t),h5(t),h6(t),h7(t)为关于变量t的函数.
综上,对于广义变系数(2+1)维Kadomtsev-Petviashvili方程(2),本文首先引入多元变换(3)和(4),将其与经典的(2+1)维Kadomtsev-Petviashvili方程(1)联系起来,通过确定多元变换中的待定系数,将变系数方程(2)约化为常系数方程(1).借助Hirota双线性方法,再结合多元变换(3)和(4),构造出方程(2)的单孤子解(22)、双孤子解(25)以及N孤子解(28),并将解中的参数赋以特殊值,勾勒出具有代表性的单、双孤子解的三维波形图及二维平面上的密度图,从而贴近实际地展现孤波的波动特征,为进一步研究孤波的各种物理性态打下基础.

