变系数波方程系统的能观测性不等式

白忠玉

（海口经济学院 网络学院，海南 海口571127）

0 引言

考虑变系数波方程：

其中Ω⊂ℝn（n≥2）是具有C2边界Γ的非空有界开区域，ν是Γ上的单位外法向量，∂i（aij∂j）是二阶椭圆微分算子，aij=aji∈C1（［0 ，+∞）；W1，∞（Ω） ）∩W1，∞（Ω×［0 ，+∞） ），存在常数λ＞0，使得

关于波方程系统的能控性问题，许多学者进行过研究.文献［1-3］在Dirichlet或Neumann边界控制下，用黎曼几何方法建立了波方程的可观测性不等式.文献［4］用乘子法和紧唯一性，证明了弹性波动方程的内部可观测性.文献［5-6］主要使用Riesz基性质和紧致微扰方法，考虑了耦合波方程的边界可控性与可观测性.文献［7］利用相同的控制函数，研究了阻尼波动方程的精确可控性.文献［8-12］研究了具有运动边界区域的波方程的可观测性和可控制性.文献［13-14］讨论了非圆柱域上具有混合边界条件的波方程的可控性.

受文献［1-4］的启发，本文讨论了更一般的情形，在Neumann边界的一些几何条件下，建立了系统（1）的能观测不等式.

1 预备知识

系统（1）的对偶系统：

解的能量定义为

且

取定点x0∈ℝn，令记边界Γ上两个不相交的开集Γ1，Γ2分别为

设η，ε＞0，μ≥0，∀ζ∈ℝn，使得

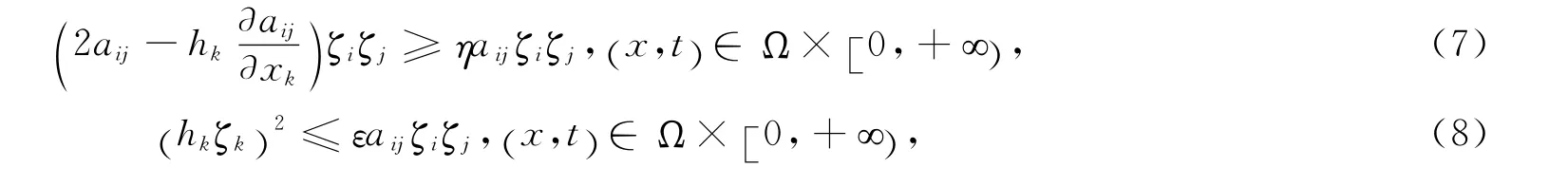
及

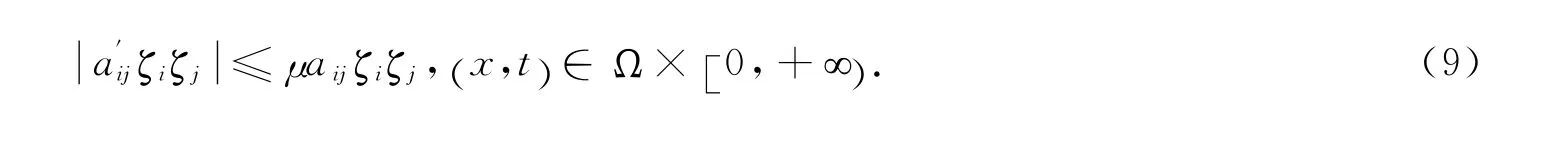
令

使

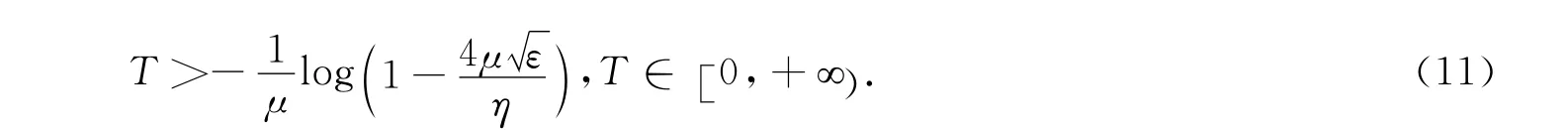
当μ=0时，取

2 主要结果及证明

首先，证明下面的引理.

引理1

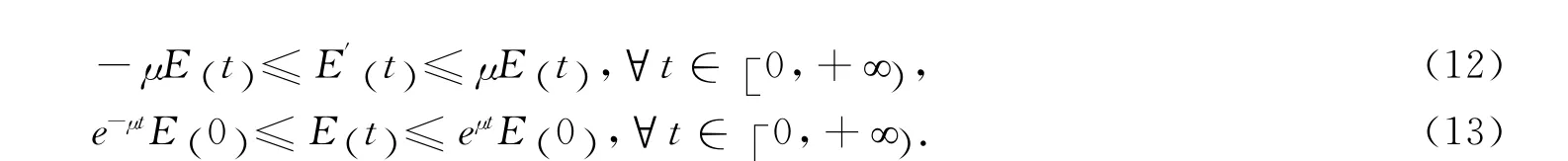
证明 由（4）、（5）和（9），得（12）.

利用Gronwall不等式，从（12）可推出（13）.

定理1若（2）、（6）、（10）和（11）成立，则存在两个正数C，C′，使得系统（3）的解满足不等式

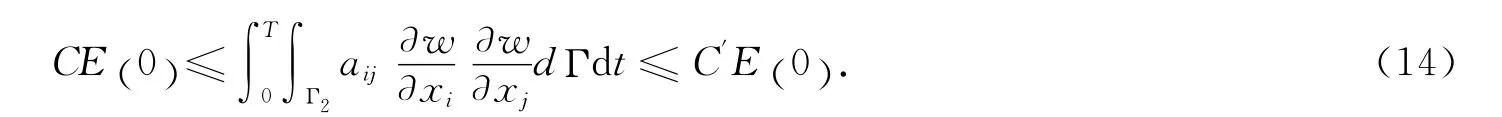
证明 任取函数p∈ （W1，∞（Ω））n和常数T＞0.由（3），得

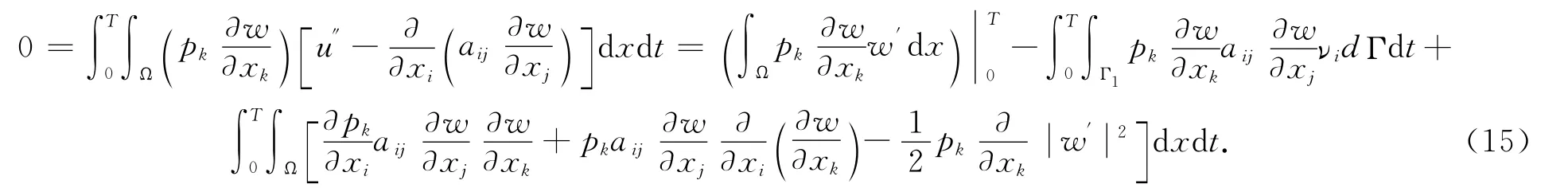
由aij的对称性，得

（15）中第二个积分的最后两项乘以2，并分部积分，得

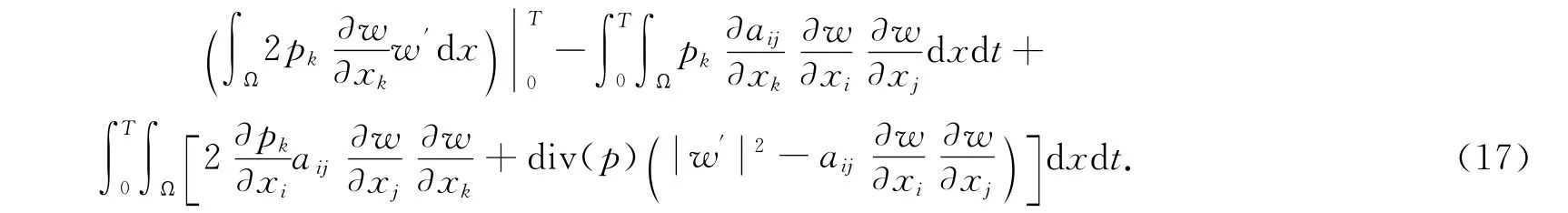
利用假设pk∈W1，∞（Ω）、aij∈W1，∞（Ω×［0 ，+∞） ）、（2）和估计（12），知（17）右边能被C0E（0）放大，其中C0＞0.

此外，由系统（3）中的齐次Neumann边界条件，有

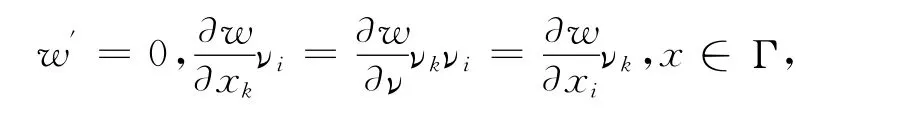
和

因此，（17）的右边化为

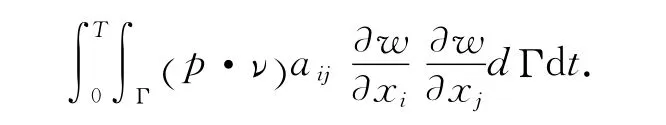
选函数p，使p=ν，x∈Γ，则（14）第二个不等式中C′=C0.

现在取pp（（x））=h（x），（17）化为

进一步，由（3）推出

由（4）、（6）和（7），得

对（18）最后一个积分，有

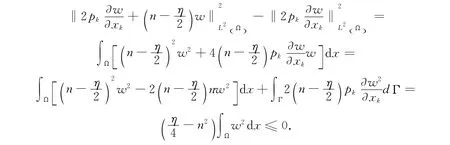
所以，由（4）、（8），得

于是，由（18）、（19），得不等式

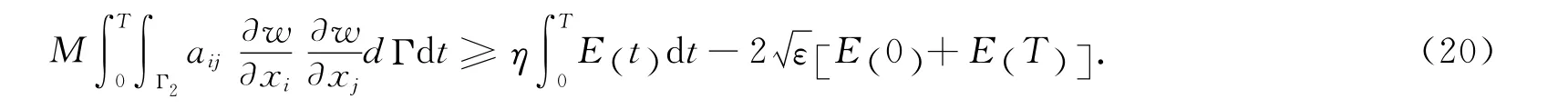
若E（T）≥E（）0，由（12），有

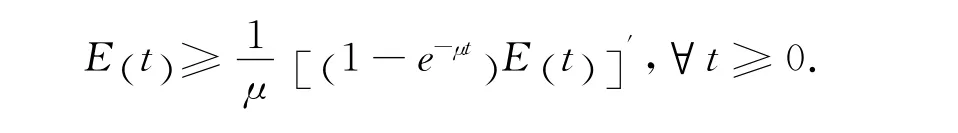
再由（20），得

和（14）式的第一个估计

同理，可讨论E（T）≤E（）0的情形，得（14）式的第二个估计.证毕.