一种非光滑函数的二阶梯度微分方程求解算法

姚爱娣，王 林

（安徽理工大学 数学与大数据学院，安徽 淮南232001）

0 引言

当前在物理学和工程学中，很多问题都可以归结为微分方程的数学形式，基于此二阶梯度微分方程求解算法也逐渐广泛地应用于函数优化、组合优化、自动控制和机器学习等科学技术领域.非滑移函数的二阶梯度微分是非滑移分析的重要组成部分，是二阶梯度微分算法优化问题研究的基础［1］.考虑到当前的经典二阶梯度微分算法缺少防滑特性，导致该算法不适用于对防滑问题的优化解决方面.在此基础上，提出了一种非光滑函数的二阶梯度微分方程求解算法，通过对各种防滑概念和微分理论进行调查分析，建立二阶梯度微分方程求解的优化算法，通过优化非光滑函数及分析力学结构特征，实现对二阶梯度微分方程求解算法的防滑性能和精准度进行提高的研究要求.

1 二阶梯度微分方程求解算法

1.1 凸函数的一阶和二阶性质定义

在二阶梯度微分方程求解算法中，必须考虑目标函数的二阶泰勒数值及凸函数性质特征，以此作为二阶导数性质研究的判断依据.在一般函数中，由于缺少特征导数，所以有必要把微分方程中的凸函数性质转换为非线性的二阶导数［2］.在进行转换的过程中，需要考虑到其收敛性x及收敛速度v，进一步结合Alexandrov定理对二阶梯度微分方程凸函数性质的一阶梯度特征和二阶梯度特征进行分析判断，并利用Mignote定理分析二阶梯度微分方程中的凸函数梯度映射参数ω和梯度的关系A，同时利用二阶梯度微分方程中的次微分外半连续性特征对凸函数的二阶广义导数进行定义，记为f（x）.进一步对差商函数的一致收敛性及其相关性特征进行规范，并制定相应的规范定理，具体如下：

定义1假设一阶梯度微分方程中的凸函数为f，在节点x∈intdomf处有一阶梯度特征展式，且满足：

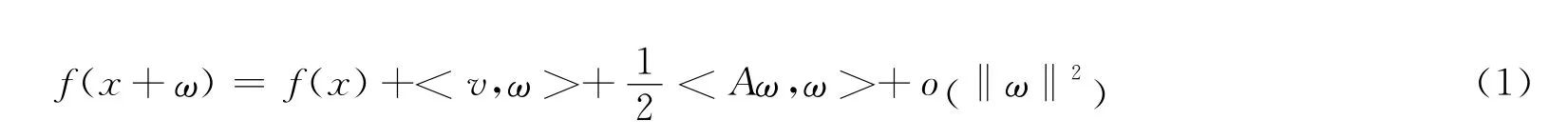
在上述算法中，凸函数的一阶偏导数几乎处处存在，若在点x∈R时，上述算法成立，则进一步在二阶偏导数在intdomf中对将凸函数次微分的外半连续性进行推导和转换，从而得到凸函数的二阶性质特征，在二阶梯度微分方程中，∂f点在函数中的定义可记为：

定义2设在二阶梯度微分方程中的凸函数收敛性能为f：Rn→R，在每个节点中都存在y∈intdomf，则有凸函数的二阶线性特征展式，具体为：

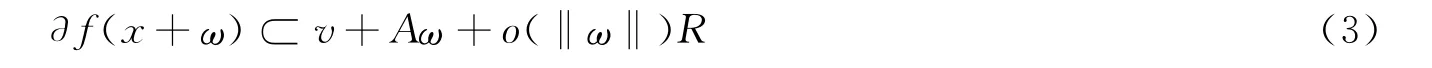
定义3进一步将gx设置为凸函数的映射函数.g表示点x的微分状态，则根据公式（1）可得u=Tv＊fx.且满足f（x+ω）≥0，b为二阶梯度微分方程中的欧氏闭环，s为雅可比矩阵.则：

定义4在符合一般微分概念的情况下，根据定理2对凸函数特征集合进行规范，记为E［3］.且满足E的取值范围始终在Dmaxf（x+ω）和Dminf（x+ω），且二者差集为零.则：

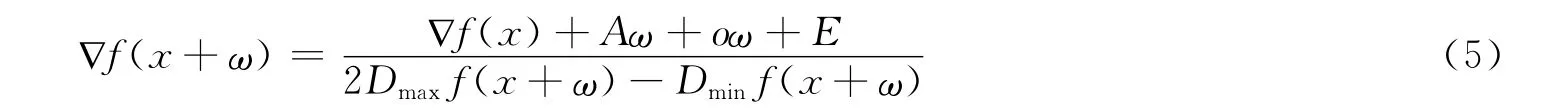
基于上述定义进行凸函数的二阶梯度特征采集和判断，以此更好地保证对二阶梯度微分方程求解的准确性［4］.

1.2 非光滑函数导数求解算法

基于凸函数的一阶和二阶性质进一步对非光滑函数的导数进行求解，通常情况下，偏微分方程存在无限多个解，在求解过程中极易出现误差，为解决这一问题，须利用非光滑函数算法在二阶梯度微分方程中添加附加条件，进行结果筛选［5］.进一步结合偏微分方程对非光滑函数导数的普遍规律进行分析，在进行导数求解的过程中，每个凸函数都存在一个方向导数，在方向导数范围内的有效域中通常缺少非凸函数，基于此需要进一步将凸函数的方向导数推导至非凸函数上，并引入一阶广义导数和非凸函数次导数的概念对其性质及相互关系进行优化，具体为：

其中，τ为凸函数在d点处沿方向，且d∈R.f°（x，d）为狭义方向导数，进一步对其广义方向导数进行求解，具体为：

进一步对其方向次导数进行求解，可记为：

进一步对二阶梯度微分方程中的完全凸函数及局部Lipschitz函数进行优化求解，若Df导数中的二元微分方向为z，凸性函数的次差为p，局部函数为k.则进一步从一阶方程的一阶展开和一阶广义展开出发，讨论二阶偏微分方程动力学模型中凸函数的非光滑性，并以一维空间中一阶偏微分方程的状态空间表示为例，分析了凸函数的性质，具体如下：

为保障研究结果的有效性，进一步对二阶梯度微分方程的边界光滑数条件进行规范，可记为：

其中，C1n（a，b）及C2n（a，b）分别表示一阶、二阶倒数中的及初始条件，且：

在上述算法中，a表示状态变量，b为无穷参数.若在进行非光滑函数导数求解的过程中z∈［a，b］，非光滑函数的偏导数的非线性项为m，ui（y）表示光滑参数，则进一步对最优导数进行筛查，具体算法为：

基于上述算法对二阶梯度微分方程的定解问题进行求解，需要先求出其一般解平滑性导数，再根据定解条件确定微分函数［6］.结合分离系数及非光滑线性算法对二阶偏微分方程进行求解，并采用傅立叶级数求解傅立叶变换积分，以此推导出一维数学物理方程的定解，并将其转化为常规微分方程，以此进一步对二阶梯度微分定解进行推导.考虑到微分方程的非光滑性特征，在求解的过程中需要对导数的二阶梯度初始条件进行反演.由于当前采用的经典方程在求解过程中，求解方法大多采用近似值模式进行定解的筛选，因此定解求导结果容易出现差异，因此需要进一步进行优化，基于一阶偏微分方程进行二阶梯度状态的求导，若一阶初始条件满足：

则进一步对非光滑函数的常规微分方程的定解进行推导，具体算法为：

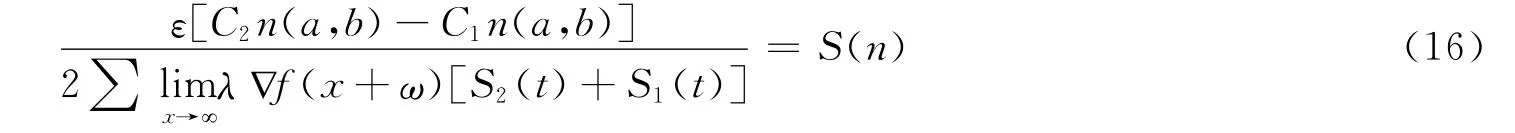
基于上述算法进行推导假设，若一阶微分方程中的微分算子是线性的，则导数的非光滑性扩散特征为线性或仿射状态，因此需要进一步对方程求解方法进行条件附加，以实现对二阶梯度微分方程的有效求解.

1.3 二阶梯度微分方程求解的实现

在二阶梯度微分方程的可行域中，结合非光滑函数算法进行目标函数值的规范计算，提高非光滑函数的适用性.在初始解条件不变的情况下，对二阶梯度微分方程特征的联合性特征进行连接，并提供相应的交换样本，从而更好地对微分交叉和变异算子进行采集计算［7］.在计算过程中易出现交叉算子部分位元交换现象，需要进行替换，以此求解非光滑函数二阶梯度微分方程的最终结果.为避免传统的求解方法中常见的惯性流变量问题，结合特征变量与线性加尔金法对求导结果进行配点比对，以提高计算精度.在二阶梯度微分方程中，若收敛性变量拟稳态为win，非光滑性动态信息特征数值为Gin，梯度惯性流动近似比为Tin.利用非光滑函数的惯量积分进行奇异性数值的建模，为提高算法有效性，对微分方程的非光滑性特征进行约束.因此需要对微分方程的非光滑特征约束算法进行优化，具体为：

其中，Δx=（x1，x2，…，xt）为非光滑导数惯性流自变量，ux=u（x1，x2，…，xj）表示未知参数，m=m1+m2+…+mt表示约束值.

进一步对最大阶偏微分方程的组阶进行计算，基于微分变量特征可知，未知参数与偏微分方程简洁性的关系，导致偏微分方程有无限多个解，为此需要对其定解预先设置定值条件.利用迭代算法实现对定解的快速逼近及误差控制处理.通过引入多个非光滑特征，进行迭代，并不断缩小取值范围，降低误差数值，具体算法为：

进一步结合非光滑函数的局限性，进行最优定解取值范围推导，具体推导原理如下：

基于上述算法，可有效实现对二阶梯度微分方程的进行多次迭代获取最优解的研究目标，更好地提高计算结果的精确度.

2 实验结果分析

为验证本文提出的非光滑函数的二阶梯度微分方程求解算法的实际应用效果，通过正交分解统计方法（即经典算法）进行对比分析，得到二阶梯度微分方程的全局离散空间基函数.结合传统的正交主元分解算法进行对比.假设，K：｛y（zi，t）｝＊Nm-n表示梯度微分方程的动态性质的测量数据，｛y（zi，t）｝N表示非光滑性特征，k｛i（za，t）｝n为奇异性数值，且可以转化约束参数，则对二阶梯度的内积时间平均值进行定义，具体如下：

进一步在有限的约束状态下进行参数调整，获取奇异值并进行非光滑性分解.将光滑性偏微分方程模型的动态正交变量进行定义，具体为：

为保障研究结果准确有效，通过电子设备进行求解计算，在计算过程中，输入两种求解算法，并分别进行计算，为保障计算结果准确，对实验设备及运行参数进行统一规范，具体如表1所示.

表1 实验参数设置

基于上表信息进一步对实验内容进行了对比分析.由于二阶梯度微分方程的求解结果常常受到静态误差和动态误差的影响，基于此，分别对两种误差影响下的计算结果进行对比记录，其中，对两种方法下的静态误差检测结果进行记录和分析，具体如图1所示.

图1 静态误差结果对比检测

基于上图检测结果进行分析不难发现，相对于经典算法而言，本文提出的非光滑函数的二阶梯度微分方程求解算法在实际应用过程中，静态误差检测数值明显更低，且收敛性也明显优于经典算法.进一步对比两种方法下的动态误差检测结果，并进行记录，具体检测结果如图2所示.

图2 动态误差对比检测结果

根据图2可以看出，本文提出的非光滑函数的二阶梯度微分方程求解算法，在计算过程中动态误差数值相对于经典算法而言，误差率相对更低且收敛性更好.基于图1、图2的检测结果进行对比分析可以发现，非光滑函数的二阶梯度微分方程求解算法在实际应用过程中，误差明显更低，由此证实，非光滑函数的二阶梯度微分方程求解算法计算结果的准确性相对更高，充分满足研究要求.

3 结语

利用非光滑函数求解二阶梯度微分方程，基本思想是：首先利用最小二乘原理，将微分方程的求解问题转化为优化问题，求出最小值，然后利用非光滑函数进行演化计算.通过算例实验进行对比检测表明，本文提出的非光滑函数的二阶梯度微分方程求解算法具有较高的计算精度，为常微分方程的求解开辟了一条新的途径，既可以得到方程的近似解析表达式，又可以准确得到定义域内任意指定位置的近似解.对比检测证实，文中提出的非光滑函数的二阶梯度微分方程求解算法具有很好的实用价值.研究证实本文提出的非光滑函数下的二阶梯度微分方程算法在实际应用过程中，具有较大的发展空间.但是，目前非光滑函数的二阶梯度微分方程求解算法的在实际应用中仍受到较多局限，算法的精度也仍有待提高，需要继续进行改进和完善.