无限维Hilbert空间中算子方程的正算子解
赵转萍
(山西工程科技职业大学,山西 太原030619)
Hilbert空间上的算子方程作为近代数学的一个重要分支一直被广泛研究,它在线性系统领域,力学和其它领域中都有重要应用.在有限维空间中,矩阵方程X+A*X-2A=Q、X-A*X-tA=I受到众多学者专家的关注,并得到了方程具有正定矩阵解的许多结论[1-4].在无限维Hilbert空间中,一些学者也给出了算子方程具有正定解的条件[5-6].本文在文献[6]的基础上进一步研究了算子方程X-s+A*XtA=B(s≥1,0<t<1),其中A,B∈B(H),B>0有正算子解的条件.
1 预备知识
设H是一个无限维可分的Hilbert空间,B(H)为H上有界线性算子集,算子A的范数、伴随算子、谱半径分别用记号‖·‖、A*,r(A)表示.
定义1设A∈B(H),如果对于任意给定的x∈H都有(Ax,x)≥0,则称A为正算子,记作A≥0.如果A是可逆正算子,记作A>0.对于B(H)上的正算子,下列结论成立:
(1)若P≥Q>0,则P-1≤Q-1.
(2)如果{Xn}是单调有界递增(减)的正算子序列,且有上界C1(下界C2),C1、C2∈B(H),则此算子序列必收敛于一个正算子.
定义2设A∈B(H),如果满足A*=A,称A是自伴算子.
定义3设A∈B(H),称σ(A)=sup{λ∈C,A-λI不可逆}是算子A的谱.
引理1[7]设P、Q是B(H)上的两个正算子,且满足P>Q,如果PQ=QP,则对一切t≥1,有Pt≥Qt.
引理2[7]设A、B是B(H)上的算子,如果A≥B≥0,则‖A‖≥‖B‖.
引理3[7]设A、T、B是B(H)上的算子,且A≥T≥B,则‖T‖≤max{‖A‖,‖B‖}.
引理4[8]设A、B是B(H)上的两个自伴算子且A≤B,则对任意的T∈B(H)有T*AT≤T*BT.
2 主要结论及证明
定理1当算子方程X-s+A*XtA=B存在可逆正算子解X时,则X满足
证明 设X为方程的可逆正算子解,
一方面,因为X-s=B-A*XtA<B,所以
另一方面,由A*XtA<B,变形得
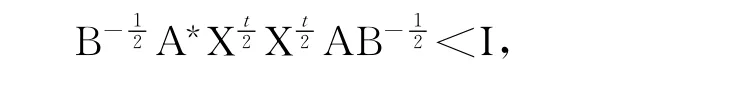
即
所以
综上可知,结论成立.
定理1给出了方程X-s+A*XtA=B存在可逆正算子解时,解的变化范围.
定理2如果当0<t<1时算子方程X-s+A*XtA=B存在可逆正算子解,那么
证明 由定理1知,AB-1A*<X-t,因此

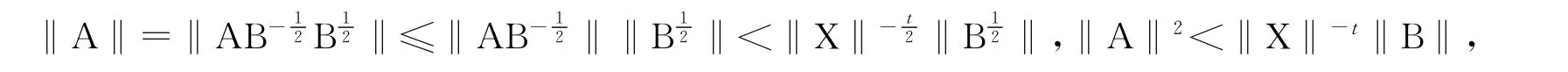
即
定理3如果算子方程X-s+A*XtA=B存在可逆的正算子解,则

证明 由方程知X-s=B-A*XtA<B,故成立,
所以
即
同理
即
因此
由引理3知
又因为A+A*是自伴算子,所以
定理4当s≥1,0<t<1时,算子方程X-s+A*XtA=B有正算子解的充要条件是存在正算子P使得P-s+A*PtA≤B成立.
证明 必要性 因为方程存在正算子解X,显然当P=X时,P-s+A*PtA≤B恒成立.
充分性 给定算子序列{Xk}:

下面利用数学归纳法证明X0<X1<…<Xk-1<Xk<P.
由P-s+A*PtA≤B知

所以
即
又因为
即
另一方面,因为X0<P,则
所以
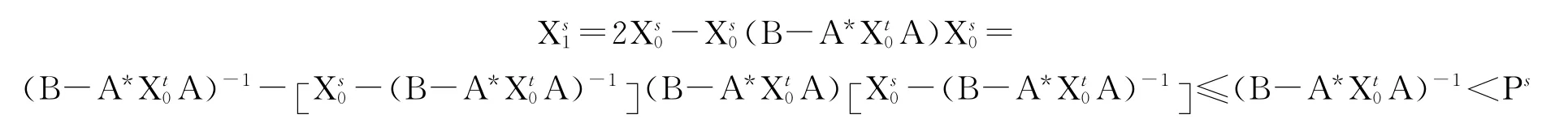
即X1<P,综上知:X0<X1<P.
假设Xk-1<Xk<P成立,下证Xk<Xk+1<P也成立.
一方面

即
另一方面,因为Xk<P,则
所以

即Xk+1<P,综上知Xk<Xk+1<P.
推论 若算子方程X-s+A*XtA=B有正算子解,则当时,

成立.
证明 由定理4中给定的算子序列知

即
所以

证毕.

