二维弹道修正弹修正机构气动特性研究

张德键,张 健,焦志刚,倪庆杰

(1.沈阳理工大学 装备工程学院,辽宁 沈阳 110159;2.辽沈工业集团有限公司,辽宁 沈阳 110045)

目前,将常规炮弹智能化,以提高射击精度、降低成本,是各军事强国研究的重点,二维弹道修正弹就是在这个契机下诞生的[1]。

与常规榴弹相比,二维弹道修正弹在结构上加装了二维修正机构,改变了二维修正弹丸外弹道运动过程中的力学特性,使二维弹道修正弹的运动更为复杂。COSTELLO[2]在1998年建立了双旋二维修正弹的七自由度刚体弹道模型,随后COSTELLO等[3]还给出了双旋弹的陀螺稳定因子和动态稳定因子的表达式。WERNERT等[4-6]对155 mm的双旋弹进行了风洞试验,得到了气动特性的变化规律,并建立了不同坐标系下双旋弹的气动模型,分析了不同坐标系下双旋弹气动参数的变化规律。JE等[7]用CFD仿真计算软件对二维弹道修正弹进行气动仿真,得到了不同马赫数和舵偏角下二维修正弹的气动特性。国内对二维弹道修正弹的研究起步相对较晚,近些年也取得了一定的研究成果。朱少雄等[8]分析了固定舵二维修正弹的气动特性,将CFD仿真计算结果和风洞实验结果进行对比,验证了CFD仿真结果的可靠性。许巍等[9]对有舵弹丸和无舵弹丸进行了数值仿真,仿真结果表明,修正结构使弹丸的升力、阻力和滚转力矩增大,从而影响了有舵弹丸的射程和散布。徐辉雯等[10]使用CFD对修正机构反旋与不旋进行了对比仿真,结果表明修正机构反旋会使阻力系数和升力系数下降,当弹丸攻角不为0时,弹丸存在侧向力。张蛟龙[11]使用CFD软件对鸭式布局双旋弹进行了仿真计算,得到了当来流速度处于亚音速、跨音速和超音速时各项气动参数的变化规律和流场分布规律。吴萍[12]设计了不同舵偏角鸭式布局二维修正弹的风洞实验。观察超音速下的纹理照片,发现弹丸头部和圆弧部出现激波,影响修正能力,对模型进行改进后,采用CFD仿真计算改进后模型的升力、阻力、滚转力矩和压心系数的变化规律。

对弹丸气动参数的研究是求解弹道方程、分析飞行稳定性的基础。现有文献中,对于二维弹道修正气动特性的研究手段,多以风洞实验和CFD仿真计算为主,在前期准备和实施过程中,需要耗费一定的时间。本文结合飞行器气动特性工程计算方法建立二维弹道修正弹的气动计算模型,引入升阻比,探究了二维弹道修正弹气动特性与舵偏角和滚转角的关系,为二维弹道修正弹结构设计和修正控制研究提供参考。

1 修正弹结构

二维弹道修正弹由修正机构和弹体组成,修正机构置于头部,装有4个固定舵偏角的舵片,两两成对,一对同向舵,一对差动舵,舵片为矩形对称薄翼。弹体分为圆弧部(尖拱形)、定心部、圆柱部(忽略弹带)和船尾部。弹体与修正机构通过滚动轴承连接,修正机构和弹体可以独立旋转,如图1所示。

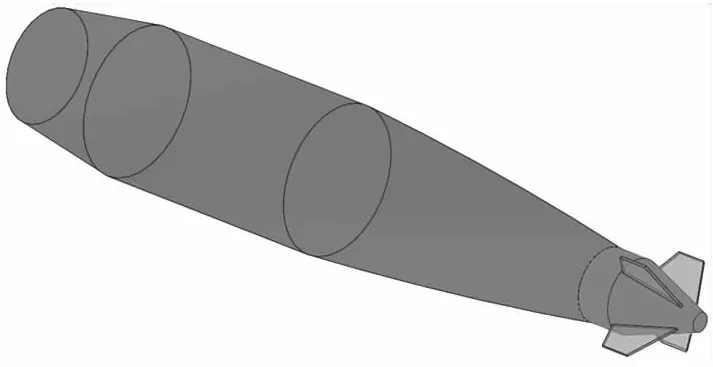
图1 二维弹道修正弹结构

2 受力分析

无控时,修正机构舵片与弹体绕弹轴高速旋转,舵片在舵机的作用下减旋且旋转方向与弹体相反。有控时,修正机构固定不转,滚转角为φ,舵偏角为δ,全弹攻角为α,弹体仍保持旋转。全弹的受力情况可视为两部分,即修正机构舵片的受力和弹体的受力。

2.1 舵片间的干扰

修正机构采用十字型舵片组合体,如图1所示,舵片两两垂直,水平方向为舵片1,同向舵,竖直方向为舵片2,差动舵。当气流通过舵片时,舵片1的下洗流平行于舵片2的翼面,则舵片1与舵片2不产生相互影响。如式(1)所示,当舵片相互垂直时,上反角ψ为45°,此时Kψ=1.0,则进行十字型翼的受力时,可单独分析一对舵片,再将两对舵片叠加。

Kψ=2cos2ψ

(1)

式中:ψ为上反角[13]。

2.2 舵片受力分析

当攻角不为0时,气流在攻角平面关于翼面不对称,舵片迎风一侧为高压区,背风一侧为低压区,总的空气动力在攻角平面内可以分解成垂直舵片面的法向力和平行于翼面与攻角平面交线的轴向力,再将法向力和轴向力向竖直方向和水平方向分解,得到舵片的升力和阻力,且升力向上为正,阻力向右为正。

一般二维弹道修正弹的两对舵片,一对为同向,舵偏角方向相同,即两侧同为正或同为负。一对差动,舵偏角方向异向,即一侧舵偏角为正,一侧为负。下面将以舵片升力为例,对舵片的受力情况进行分析。

2.2.1 正舵偏角

当舵偏角为正时,舵片的有效攻角为α+δ,如图2所示,法向力FN分解产生的升力Fy1,方向竖直向上。轴向力FA分解产生的升力Fy2,方向与Fy1相反。总升力大小Fw+=Fy1-Fy2,为方向竖直向上的正升力。

图2 舵偏角为正时舵片的受力情况

根据空气动力学线性理论,小扰动下机翼升力特性的计算方法,当舵偏角为正时,舵片升力的表达式为

Fw+=C′ypdSw(α+δ)

(2)

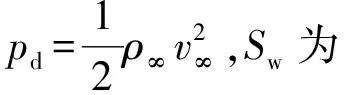
2.2.2 负舵偏角

当舵偏角为负时,舵片的有效攻角大小变为α-δ,如图3所示。法向力FN和轴向力FA沿竖直方向分解产生的升力分别为Fy1和Fy2,二者方向相反，且合力方向竖直向上,为舵片提供正升力,升力大小Fw-=Fy1-Fy2,方向竖直向上。

图3 舵偏角为负时舵片的受力情况

舵偏角为负时,舵片升力表达式为

Fw-=C′ypdSw(α-δ)

(3)

综上分析,二维弹道修正弹同向舵为2个舵片的舵偏角同为正,其升力Fwt表达式为

Fwt=C′ypdSw(α+δ)

(4)

差动舵为2个舵片舵偏,舵偏角一个为正,一个为负,其升力Fwc表达式为

整理得:

Fwc=C′ypdSwα

(5)

2.2.3 滚转角

滚转角对舵片的受力情况如图4所示。

图4 滚转角对舵片受力情况

如图4所示,滚转角对二维弹道修正弹的气动特性的影响由两部分组成,一部分为攻角与滚转角的组合,另一部分为舵偏角与滚转角的组合。

2.2.4 攻角与滚转角组合

当舵偏角为0时,将舵片的升力分解为垂直翼面1的分量FN1和平行于翼面1的分量FN2,平行于翼面1的分量FN2垂直于翼面2。FN1=Fy,wcosφ,FN2=Fy,wsinφ。再将FN1和FN2沿竖直方向分解,得到翼1和翼2的升力为

Fy,w1=Fwtcos2φ,Fy,w2=Fwcsin2φ

(6)

则舵片升力表达式为

Fw=Fy,w1+Fy,w2=C′ypdSwαcos2φ+C′ypdSwαsin2φ

整理得:

Fw=C′y,wpdSwα

(7)

2.2.5 舵偏角与滚转角组合

当攻角为0时,舵片1为同向舵,舵片2为差动舵,左右两片差动舵产生的升力方向相反,数值相同,此时的升力仅由舵片1提供,舵片的升力表达式为

Fw=Fy,w1+Fy,w2=C′ypdSwδcosφ

(8)

综上,当考虑舵偏角和滚转角时,修正机构舵片升力系数为

Cy,w=C′y,w(α+δcosφ)

(9)

式中:a+δcosφ为舵片的合攻角。

2.3 弹体的受力分析

二维弹道修正弹弹体为旋成体,当攻角不为0时,其受力情况与普通榴弹相同,可参考文献[14]。

3 气动力计算

3.1 升力系数

弹翼之间存在相互干扰,致使二维弹道修正弹的升力系数不单纯等于弹体升力系数与舵片升力系数之和,计算过程中需要考虑干扰的影响。当攻角不为0时,通过舵片的气流在舵片上下表面形成了一个压力差,使舵片产生升力。同时气流通过舵片产生的自由涡系和附着涡系映射在弹体内部形成的镜像涡系,使弹体产生了附加升力,这个附加升力就是舵片对弹体的干扰升力。

同样,弹体对舵片也造成一定干扰,当气流的垂直分量v∞sinα通过弹体时,在弹体两侧形成了上洗流,越靠近弹体,上洗流速度越大。在舵片和弹体结合位置,靠近弹体的上洗流作用在舵片上,对舵片的升力产生干扰。

综上,可得二维弹道修正弹升力系数为

Cy=Cy,B+(Cy,wSw/Sm)

(10)

式中:Cy,B为弹体的升力系数,Cy,w为矩形舵片的升力系数,Sm为弹体横截面积。

(11)

式中:Kα和Kδ为干扰因子,求解公式根据参考文献[13]为

(12)

式中:舵片所在位置弹体直径D与舵片展长l之比s=D/l。若设舵片展长为定值,可通过s的值分析舵片安装位置对全弹气动特性的影响。若舵片安装位置为定值,则可通过s的值分析舵片展长对全弹气动特性的影响。

3.2 阻力系数

全弹的阻力系数等于零升阻力系数与诱导阻力系数之和,加装了修正机构后,其零升阻力可视为弹体零升阻力系数加上舵片的零升阻力系数,诱导阻力也可视为弹体诱导阻力系数加上舵片的诱导阻力系数。

Cx=Cx0B+(NCx0wSw/Sm)+CxiB+(CxiwSw/Sm)

(13)

式中:Cx0B为弹体的零升阻力系数;Cx0w为单独舵片的零升阻力系数,等于舵片的摩阻与波阻之和;N为舵片数(对);CxiB和Cxiw分别为弹体的诱导阻力系数和单独舵片的诱导阻力系数,舵片的诱导阻力系数包含弹体对舵片干扰产生的诱导阻力和舵片对弹体干扰产生的诱导阻力。

3.3 可靠性分析

以某型号固定翼二维弹道修正弹为算例,计算二维弹道修正弹气动特性随马赫数的变化规律,与CFD仿真结果进行对比,验证工程算法的可靠性。

全弹的结构参数:弹径D=0.122 m,弦长b=0.046 2 m,舵片面积Sw=0.004 6 m2,弹体最大横截面积Sm=0.011 7 m2,弹体横截面积与侧面积之比Sc=11.067 6,长径比λ=5.97,弹头部长径比λn=3.2,圆柱部长径比λc=2.06,弹尾部长径比λt=1.0,弹尾收缩比st=0.5,根梢比η=1.0,展弦比λw=2.16,声速为340 m/s,舵片数2对。

当攻角α=6°,舵偏角δ=4°,径展比s=0.5,升力系数、阻力系数随马赫数的变化曲线如图5所示。从图5可以看出,随着马赫数的增大,升力系数呈先增大后减小再增大的变化趋势,阻力系数呈先增大后减小的变化趋势。将计算得到的升力系数曲线、阻力系数曲线与CFD仿真结果对比,升力系数的误差为8.1%,阻力系数的相对误差为9.5%,均小于10%,对于二维弹道修正弹气动计算模型,满足计算的可靠性。

图5 气动力系数与马赫数关系图

分析产生误差的原因:进行工程计算时设置的环境参数为定值,致使雷诺数等参数在计算时存在一定误差;在工程算法中的需要查公式中的系数(如弹体的法向力系数)与弹丸结构的关系图,查图存在一定误差;对于跨音速段的忽略也会造成一定的误差。

4 舵偏角和滚转角的影响

4.1 升阻比

为分析舵偏角和滚转角对二维弹道修正弹气动特性的影响,引入二维弹道修正弹升阻比ζK=Cy/Cx。

当二维弹道修正弹以最大的升阻比运动时,其气动效率最好,气动能力最佳[15]。

遗传算法是一种模拟生物进化过程的计算模型,是一种搜索最优解的方法[16]。基于遗传算法,对在舵偏角δ=0°且无控时的二维弹道修正弹的最大升阻比和最佳攻角进行寻优。设置种群数为1 000,进化代数为60,交叉概率为0.7,变异概率为0.01。求解结果,最大升阻比约为1.45,对应的最佳攻角约为13.7°,如图6和图7所示。

图6 遗传算法图像

图7 升阻比与攻角关系图

4.2 舵偏和滚转的影响

4.2.1 舵偏角的影响

图8为修正机构舵片的舵偏角对二维弹道修正弹最大升阻比和最佳攻角的影响。由图可知,通过对比遗传算法的寻优结果,随着修正机构舵偏角的增大,二维弹道修正弹的最大升阻比在减小,对应的最佳攻角也在减小。由此可知,当攻角较大时,较小的舵偏角可使二维弹道修正弹获得更高的气动效率和更好的气动能力。当攻角较小时,较大的舵偏角可使二维弹道修正弹的气动效率和气动能力更好。当进行修正时,攻角越大,可控制舵偏角变小;若修正时攻角较小,可控制舵偏角变大。以保证修正时,弹丸有最好的气动能力。

图8 舵偏角与升阻比关系图

4.2.2 滚转角影响

采用遗传算法对修正机构有控时(修正时)的滚转角进行寻优,如图9所示。

图9 最佳滚转角

图9为攻角和舵偏角固定时,升阻比、滚转角和最佳攻角关系图。当滚转角为180°时，全弹的升阻比最大。考虑滚转角后,二维弹道修正弹全弹的升阻比随攻角变化规律如图10所示。

图10 滚转角与升阻比关系图

从图10可以看出,当攻角小于8°时,无控的二维弹道修正弹全弹具有更大的升阻比,当攻角大于8°时,滚转角为180°时,二维弹道修正弹全弹具有更大的升阻比。最大升阻比对应的最佳攻角出现在攻角大于10°的区域,且其数值均大于无控时的数值。由此可见,当滚转角处于180°时,二维弹道修正弹具有更好的气动效率和气动能力,此时对弹道的纵向修正效果更好。

5 结束语

本文通过对二维弹道修正弹进行受力分析,采用飞行器气动特性工程计算方法,对二维弹道修正弹升力和阻力进行了仿真计算,分析了其力学特性的变化规律。计算结果与CFD仿真结果对比,相对误差不大于10%。综上说明本文使用的气动计算模型能够用于计算二维弹道修正弹的升力系数和阻力系数,分析结构参数对其气动特性的影响,可为二维弹道修正弹气动特性的研究和结构设计提供参考。

基于遗传算法,分析了修正机构舵偏角和滚转角对二维弹道修正弹气动特性的影响。得出如下结论:全弹的最大升阻比和最佳攻角均随修正机构舵偏角的增大而减小。当攻角较小时,舵偏角越大,全弹的气动效率越好,气动能力越好。若修正时,攻角较大,可控制舵片的舵偏角变小,攻角较小时修正,可控制舵偏角变大,使二维弹道修正弹在修正时气动能力处于最佳状态,以达到最佳的修正效果。在进行修正时,全弹的最大升阻比出现在滚转角为180°时,且在攻角大于10°时,全弹的升阻比更大,气动效率更高,弹道纵向修正能力更好。