弹道修正迫弹制导方法与制导精度研究

孙希彤,罗兴柏,高 敏,周晓东

(陆军工程大学 1.弹药工程系;2.导弹工程系,河北 石家庄 050003)

迫击炮弹是陆军步兵极其重要的常规武器,是伴随和支援步兵作战的压制性武器,能够打击敌前沿、浅近和一定纵深的各类有生力量,装甲目标及炮兵阵地。现役迫击炮弹多为无控,受各类随机干扰影响,落点散布大,难以满足现代战争需要[1]。迫击炮弹制导化改造成为了当下发展的重要方向,制导迫弹由于空间体积有限,制导元件有限且多小型化。控制执行机构以小体积的气动力执行机构居多,探测元件采用卫星接收器、惯导及导引头复合的方式[2]。伴随着迫击炮弹硬件上的制导化改造,各类制导方法层出不穷。

文献[3-4]在传统比例导引的基础之上,根据目标特性和作战要求,设计偏置项,实现对攻击角度的约束,达到大落角攻顶的目的。文献[5-6]研究了摄动落点预测制导方法在制导弹药上的应用,分析了摄动落点预测基本原理,设计了相关仿真试验,验证了算法的有效性。文献[7-8]以弹道修正炮弹为研究对象,应用落点预测制导算法,采用卡尔曼滤波进一步提高预测精度,仿真验证得出落点预测算法可以有效提高落点精度。文献[9-13]基于传统的比例导引算法,针对制导弹药战技指标要求,分别从撞击角度约束、视场角度约束、过载约束、初始前置角等条件出发,采用过重力补偿、偏置项改进、拦截角模型设计等方法,对比例导引算法进行改进,仿真验证了所设计算法的有效性。文献[14-15]采用最优制导律或滑模控制等方式,针对落角约束、姿态约束等要求,对制导算法进行研究设计并验证,但该类算法比较复杂,需求参数较多,对硬件要求较高,对于低成本的制导弹药来说并不适合工程应用。

摄动制导和比例导引可以有效提高制导迫弹射击精度,但目前摄动制导主要围绕预测偏差的收敛速度、准确度及单独使用摄动落点偏差制导律的制导效果方面的研究。比例导引的研究中,如前所述,多围绕约束条件或运用最优控制等理论设计比例导引律,主要用于目标机动或落角约束的情况。对于打击地面固定目标且弹道弯曲的迫击炮弹来说,通常不必进行复杂设计。为实现由卫星和惯导进行探测的组合导航制导迫弹弹道修正的工程应用,本文基于比例导引,设计了纵向平面自适应比例导引和横向平面自适应比例微分导引。对比分析摄动落点偏差预测法、自适应比例导引法、自适应比例微分导引法在弹道横、纵向平面的修正效果。设计了复合修正算法,采用蒙特卡洛模拟打靶仿真对比了几种算法的修正效果。

1 弹丸运动模型建模

1.1 弹丸质心运动的动力学方程

在弹道坐标系中建立的弹丸质心运动的动力学方程为

(1)

式中:m为弹丸质量;v为弹丸速度;θ为弹道倾角;ψV为弹道偏角;Gx2,Gy2,Gz2为重力在弹道坐标系下的分量;Fx2,Fy2,Fz2为空气动力在弹道坐标系下的分量。

1.2 弹丸绕质心转动的动力学方程

在准弹体坐标系中建立的弹丸绕质心转动的动力学方程为

(2)

式中:Jx4,Jy4,Jz4为弹丸对于准弹体坐标系各轴的转动惯量;ωx4,ωy4,ωz4为转动角速度ω在准弹体坐标系各轴上的分量;Mx4,My4,Mz4为空气动力矩在准弹体坐标系的分量。

1.3 弹丸质心运动的运动学方程

(3)

式中:x,y,z为惯性系下弹丸在3个坐标轴上的坐标。

1.4 弹丸绕质心转动的运动学方程

制导迫弹转速较低,通常为几转,因此在时间很短的情况下,认为转动角速度是常值,可由角度求导而得:

(4)

式中:ϑ为俯仰角,ψ为偏航角,γ为滚转角。

1.5 几何关系方程

(5)

式中:α为攻角,β为侧滑角,γv为速度倾斜角。

1.6 控制关系方程

迫击炮弹采用双通道舵机实现制导控制,舵机由两对舵片组成,不控滚转。通过弹载角速率陀螺测量滚转角γ,根据滚转角γ,建立弹体坐标系x1y1z1和准弹体坐标系舵偏角的转换关系,得到实际输出的舵偏角指令:

(6)

式中:δy1,δz1为弹体系下需用舵偏角;δy4,δz4为准弹体系下需用舵偏角。

受机械结构的限制,舵片偏转最大幅值限制,当所需偏转幅值超过最大幅值δmax时,对δy4,δz4进行限幅:

(7)

2 摄动落点偏差预测制导方法

在只考虑影响射程偏差和横向偏差主要因素条件下,射程偏差ΔL和横向偏差ΔH的计算公式为

(8)

式中:L为射程函数;H为横向偏差函数;vx,vy,vz为弹丸在惯性系3个坐标轴上的速度分量;Δvx,Δvy,Δvz,Δx,Δy,Δz为舵机作用Δt时间后相应参数在惯性系各坐标轴上的分量。

摄动落点偏差预测制导方法的纵向平面制导回路以ΔL为控制变量,横向平面制导回路以ΔH为控制变量。俯仰舵控角和偏航舵控角的计算方法为

(9)

式中:kL为纵向放大系数,kH为横向放大系数,K1为导引系统增益。

3 比例导引律

3.1 比例导引律制导原理

弹丸与目标点在惯性系纵向平面内的相对运动关系如图1所示,假设目标点为T,坐标为(xt,yt),M代表弹丸的实时位置,q为视线角。

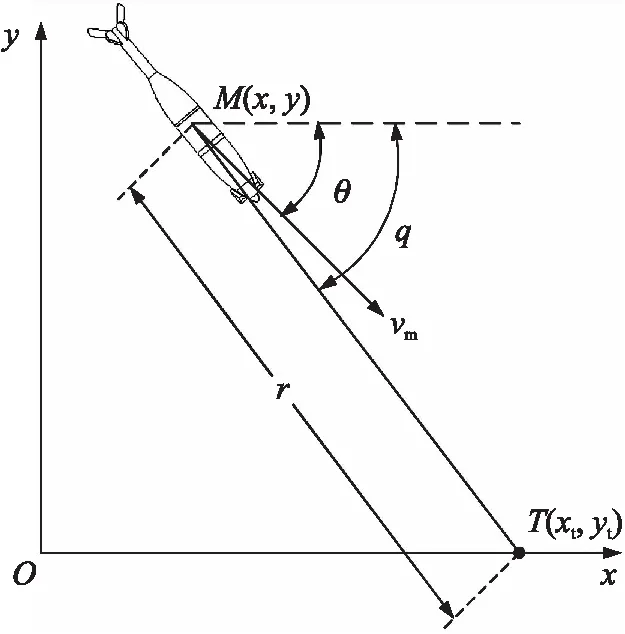
图1 弹目关系示意图

根据比例导引律定义,弹丸速度转动角速率与视线旋转角速率成正比,即应满足:

(10)

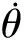
(11)

式中:Δx,Δy,Δz为弹丸位置与目标点位置的偏差;d为弹目距离;vx,vy,vz为弹丸速度。

对式(10)进行积分,为便于计算制导信息,将θ记为指令弹道倾角θc,ψV记为指令弹道偏角ψVc,得:

(12)

式中:θ0,ψV0分别为比例导引开始时的弹道倾角和弹道偏角;qL0,qH0分别为比例导引开始时的纵向平面弹目视线角和横向平面弹目视线角。

通过速度信息计算弹道倾角和弹道偏角的公式为

(13)

根据弹丸弹道倾角、弹道偏角和指令弹道倾角、指令弹道偏角的差值计算纵向、横向制导信号:

(14)

式中:Uθ为纵向制导信号,UψV为横向制导信号。

纵向平面制导回路以Uθ为控制变量,横向平面制导回路以UψV为控制变量,俯仰舵控角δz和偏航舵控角δy的计算方法为

(15)

(16)

式中:KM为弹丸传递系数,kL为纵向放大系数,kH为横向放大系数。

比例导引律中,横、纵向放大系数采用定值,得到的俯仰舵控角并不能在每时刻都最大限度地减小Uθ,进而导致指令弹道倾角不符合弹道倾角变化规律,降低了制导效率。

3.2 纵向平面自适应比例导引律

本节对比例导引律形成的指令弹道倾角不符合弹道倾角变化规律的原因进行分析,提出一种纵向平面自适应比例导引律。

假设弹丸在接近目标过程中弹道倾角变化率与视线角速率成如下关系:

(17)

式中:k′PL为真实弹道所需的比例系数。则实际的弹道倾角可表示为

θ=θ0+k′PL(qL-qL0)

(18)

将式(12)和式(18)代入式(14),可得:

Uθ=(k′PL-kPL)(qL-qL0)

(19)

弹丸的俯仰舵控角可表示为

δz=-kLK1(k′PL-kPL)(qL-qL0)

(20)

式(15)中kL和K1是根据弹道特性设定的,弹目视线角的变化值(qL-qL0)虽然受控制的影响,但是弹道修正迫击炮弹的外弹道相对稳定,弹目视线角的变化(qL-qL0)主要由弹丸与目标的相对运动特性决定。需用过载与俯仰舵控角是对应的,因此需用过载主要取决于比例系数kPL和实际弹道中比例系数k′PL的差别。

分别将大射程(6.7 km)弹道与小射程(2.0 km)弹道的落点设为目标点,计算迫击炮弹接近目标过程中弹道倾角变化率与视线角速率的比值,如图2所示。可以看出,大射程时,弹道倾角变化率与视线角速率比值变化平稳,进入降弧段时为-2.391,弹丸落地时约为0;小射程时,弹道倾角变化率与视线角速率比值变化幅度较大,进入降弧段时为-17.25,弹丸落地时约为0。

弹道修正迫击炮弹弹道弯曲特性明显,从图2可以看出,弯曲弹道导致弹道倾角变化率与视线角速率比值不断变化,对比例导引律指令比值的及时跟进提出了要求。若指令比值与实际比值差别较大,必然降低修正能力,增大落点偏差,针对这一问题,提出一种自适应比例导引律。

图2 弹道倾角变化率与视线角速率比值

3.3 自适应比例微分导引律制导原理

形成横向平面散布的主要因素是射向偏差,横向落点偏差的形成特点是横向落点偏差随飞行时间的增加而逐渐增大,因此减小横向平面落点偏差的有效方式是减小横向位置偏差的同时迅速减小横向速度。因此,横向平面采用自适应比例微分导引律。比例微分导引律中横向制导信号的计算方法为

UψV=kPz+kPtDvz

式中:kP为比例系数,tD为微分时间常数,vz为横向速度,由弹载导航设备测出。

实施横向控制的目的是减小横向落点偏差,而横向速度造成的横向落点偏差与剩余飞行时间有关,因此令微分时间常数等于剩余飞行时间,实现微分时间常数的自适应变化。即

tD=tgo

式中:剩余飞行时间tgo=d/vm,d为弹目距离;vm为迫弹实时速度,可通过组合导航测量得出。

偏航舵控角的计算方法为

δy=-kHK1UψV

4 仿真分析与飞行试验

4.1 模拟打靶中仿真状态的设定

为使模拟打靶的射程以及弹道特性具有代表性,目标射程定为6.7 km,初速为334 m/s,海拔设为265 m,气象采用炮兵标准气象条件。根据目标射程搜索射角为45°,射向为基准射向右偏0.13°。通过在6.7 km射程标准弹道状态上加入各项干扰得到模拟打靶各弹道状态。模拟打靶采用的各项干扰及其分布律如表1所示,表中3σ为各干扰项正态分布的三倍均方差。

表1 干扰项列表

根据以上的模拟打靶流程模拟打靶100次,得到模拟打靶结果见图3。将本次模拟打靶每条弹道(共计100条)的各项干扰的取值记录下来,之后有控模拟打靶各项干扰使用本次记录的数值。确保有控打靶和无控打靶时干扰项相同,剔除干扰项数值不同对落点精度的影响。

图3 无控弹模拟打靶结果

模拟打靶结果显示,弹丸纵向落点偏差范围为-314.461 9～275.860 3 m,横向落点偏差范围为-182.391 4～148.703 4 m,纵向落点偏差标准差为126.535 4 m,横偏落点偏差标准差为84.996 4 m,圆概率误差为126.317 m。

4.2 弹道修正效果仿真

4.2.1 横向修正精度打靶仿真

为避免纵向平面的影响,将纵向平面置为无控。启控条件设为飞行时间≥10 s启控。横向平面分别采用摄动落点偏差预测制导方法、固定系数比例导引律、自适应比例微分导引律进行模拟打靶,舵片偏转最大幅值δmax设定为15°。

几种制导方法的放大系数或者比例系数并无严格的理论计算方法,只能通过设定不同的系数进行模拟打靶,根据打靶精度优选出合适的系数。经过分析,最终确定在横向平面修正时,摄动落点偏差预测制导方法中,kH=0.05;固定系数比例导引律中,kPH=5;比例微分导引律中,令kH=0.05,kP=1,模拟打靶结果如图4和表2所示。采用自适应比例微分导引时的横向标准差最小,100%的落点偏差被修正到-1.5～2.5 m以内,横向标准差为0.660 4 m。

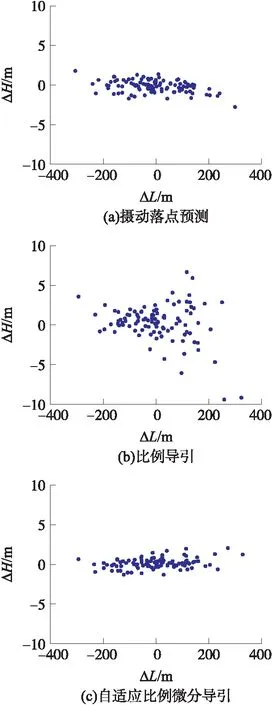
图4 横向落点散布

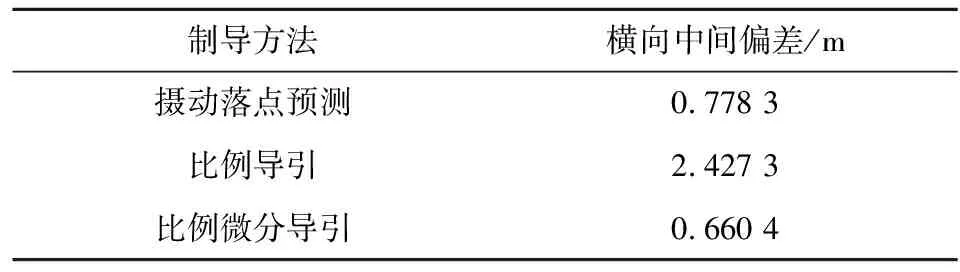
表2 横向落点散布参数

4.2.2 纵向修正精度打靶仿真

为避免横向平面的影响,将横向平面置为无控,启控条件为进入降弧段启控。纵向平面分别采用摄动落点偏差预测制导方法、固定系数比例导引律、自适应比例导引律进行模拟打靶,结果如图5和表3所示。自适应比例导引律采用的比例系数数组按图5所示确定,摄动落点偏差预测制导方法中,kL取0.05;固定系数比例导引律中,kPL取-4.8。

图5 纵向落点散布

表3 纵向落点散布参数

从图5和表3可知,采用自适应比例导引律时的纵向落点散布最小,绝大多数落点偏差被修正到5 m以内,纵向落点偏差比较大的点也得到了充分修正,从结果中可知,自适应比例导引的方法误差最小。

4.2.3 复合制导打靶精度仿真

当同时修正纵向平面和横向平面时,还需研究采用何种复合制导算法。从前述仿真可知,横向平面采用自适应比例微分导引律取得的制导精度最高。纵向平面降弧段自适应比例导引制导效果优于比例导引的制导效果。但摄动落点偏差预测制导方法与自适应比例导引律共同进行纵向修正,以及各自与自适应比例微分导引律结合进行修正,还需再次讨论。

①纵向平面采用摄动落点偏差预测制导方法,横向平面采用自适应比例微分导引律。

②纵向平面升弧段无控,纵向平面降弧段采用自适应比例导引律;横向平面采用自适应比例微分导引律。

③纵向平面升弧段采用摄动落点偏差预测制导方法,纵向平面降弧段采用自适应比例导引律;横向平面采用自适应比例微分导引律。

启控时间定为10 s。纵向平面采用2种制导方法时,升弧段制导方法交班至降弧段制导方法的条件为vy<-10 m/s,以避开弹道顶点,避免引起弹丸飞行稳定性问题。上述5种复合制导算法的打靶结果如图6和表4所示。

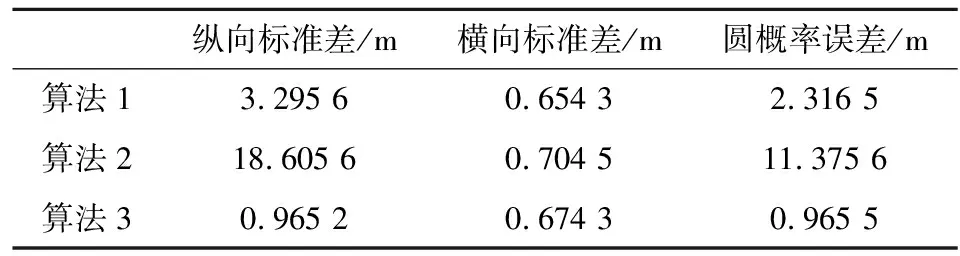
表4 复合制导算法落点散布参数

图6 不同复合制导算法的打靶结果

复合制导算法3的打靶结果要明显优于其他复合制导算法的打靶结果。复合制导算法2中纵向平面采用摄动落点偏差预测制导方法,个别弹道的纵向落点偏差较大,存在一定的方法误差。复合制导算法3的圆概率误差为0.965 5 m,制导方法误差最小。因此,弹道修正迫击炮弹应采用复合制导算法3,即纵向平面升弧段采用摄动落点偏差预测制导方法,纵向平面降弧段采用自适应比例导引。

迫击炮弹射角范围通常在45°～80°之间,弹道呈现大弯曲特性,复合制导算法是在迫击炮弹45°射角且大射程条件下进行的验证。为验证小射程条件下复合制导算法3的有效性,设定初速为270 m/s,射角为78.91°,海拔设为265 m,气象采用炮兵标准气象条件,目标射程为2.0 km,启控时间10 s,采用表1各干扰项进行模拟打靶,打靶结果如图7和表5所示。

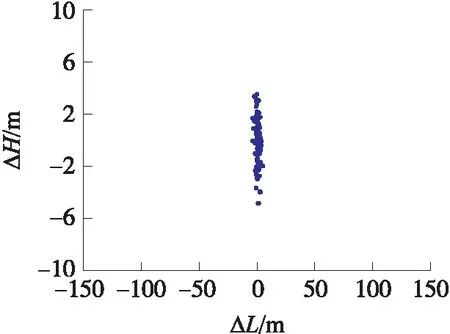
图7 小射程模拟打靶结果

表5 小射程落点散布参数

由表5可知,小射程下复合制导算法3模拟打靶的圆概率误差为1.864 3 m,比大射程模拟打靶圆概率误差略大,这是由于小射程弹道较弯曲,增加了制导的压力所致。不过制导算法在大射角、小射程下,仍具有较好的制导精度。

三次仿真试验的结果表明,所提出的几种制导方法在制导迫弹6.7 km射程下,横、纵向平面都能够起到修正偏差、提高精度的效果。其中,自适应比例微分导引律在横向平面的修正效果优于其他制导方法,横向中间偏差减小到0.660 4 m。纵向平面的仿真中,自适应比例导引的修正效果最好,纵向中间偏差缩小为16.059 2 m,比例导引律修正效果明显不如自适应比例导引律的修正效果,纵向中间偏差达到46.829 8 m,说明弹道倾角变化率与视线角速率指令比值不能很好地跟进实际比值,将会带来落点偏差的增大。复合制导仿真表明,摄动落点偏差预测法、自适应比例导引法、自适应比例微分导引法复合制导方式,可以迅速降低落点偏差,提高制导精度,横、纵向偏差及圆概率误差都小于1 m。通过大射角且小射程模拟打靶,验证了复合制导算法3同样具有较好的制导精度。

5 结束语

本文给出了摄动落点预测制导方法,基于比例导引法,结合弹道特点,在降弧段弹道,纵向平面构建了自适应比例导引,横向平面构建了自适应比例微分导引律。通过横向平面仿真,自适应比例微分导引律修正效果最好,横向中间偏差为0.660 4 m。通过纵向平面仿真,自适应比例导引修正效果最好,纵向中间偏差为16.059 2 m。结合以上制导律,设计复合制导并仿真,结果表明,纵向平面升弧段采用摄动落点偏差预测制导方法,降弧段采用自适应比例导引律,横向平面采用自适应比例微分导引律的制导效果最好,圆概率误差从无控时的126.317 m降为0.965 5 m。大射角且小射程条件下模拟打靶,圆概率误差为1.864 3 m。