弹丸三维速度实时处理方法研究
段鹏伟,宫志华,吕海东
(中国人民解放军63861部队,吉林 白城 137001)
弹丸飞行速度一直是武器试验参数中的一项重要测试内容,是弹道学中不可缺少的基础参数[1],对武器系统定型、射表编拟及弹道理论研究等都具有重要的意义[2]。尤其是随着高新技术的不断发展及其在军事领域中的广泛应用,各种新型武器也逐渐更新换代,以末敏弹、修正弹和制导弹等为代表的智能武器弹药[3]鉴定也成为常规靶场试验的重点。在这些智能武器弹药的试验鉴定中,弹丸的实时三维速度已经成为不可或缺的测量参数,它不仅是判断弹丸飞行状态的主要依据,更重要的是它能够迅速、准确地反映弹丸的实时控制状态和效果;同时它还是安控系统的重要输入参数,其精度直接影响安控系统的辅助判决,进而影响到试验指挥决策。目前,大部分常规武器靶场的测控系统仍然是以弹丸位置信息为主要弹道信息,仅粗略计算弹丸的实时三维速度,这导致无法及时有效地对弹丸测控形成反馈,严重影响指挥系统做出正确判断和决策。在数据融合的研究方面也存在相似的现象,大部分学者主要以目标位置信息为研究对象,对目标速度的数据融合研究相对较少[4]。在常规武器靶场,宫志华等[5]提出了一种基于光雷组合测量的弹丸高精度切向速度求取方法,但是该方法主要用于事后弹道数据融合处理,不适用于实时处理。在航天靶场,李果等[6]提出了短基线干涉仪与测速设备相结合的数据融合处理方法,获得了目标的位置和速度参数,但是在模型的建立过程中,精确获取目标相对测站的角速度较为困难,不易于工程实践。
因此,本文提出将多个测站测得的弹丸径向速度与弹丸位置信息进行二次实时数据融合处理,实现了常规靶场测控系统弹丸三维速度的实时高精度数据处理。
1 数据融合模型构建
在靶场现有测控系统中,对测控弹丸的位置信息进行实时融合处理时,弹丸的径向速度仅作为辅助信息,不参与实时融合处理,这就造成信息资源的浪费,也导致实时融合处理得到的弹丸三维速度精度较差。为了提高弹丸三维速度的解算精度,以弹丸位置信息和精度较差的三维速度为初值,弹丸位置信息和实时径向速度作为观测量,建立以弹丸位置误差和速度误差为待估参数的融合模型[7-8]。
设测站的坐标为(xco,yco,zco),当前时刻目标的坐标真值为(x,y,z),则目标距离可表示为
(1)
取目标坐标初值为(x0,y0,z0),将方程在(x0,y0,z0)处进行线性化展开得到距离误差方程。
(2)
式中:Δx,Δy,Δz分别为目标三维位置初值相对于真实值的误差;R0为目标距离初值。
对式(2)进行偏微分,可以得到径向速度误差方程:
(3)
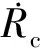
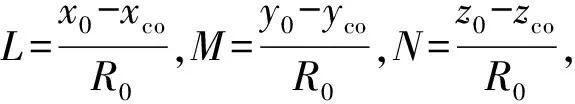
(4)
将n个测速设备的测量值误差与三维位置信息误差联立,形成求取三维位置和三维速度的融合模型。
δc=AΔX
(5)

误差方程待估参数设计矩阵为
在式(5)所示的融合模型矩阵方程中,为保证其解的唯一性,取P为权系数矩阵,可采用各测速设备随机误差方差的倒数的对角阵作为权系数矩阵,以最小二乘为准则,求取待估参数向量也就是三维位置和速度的误差,用误差向量再对三维位置和速度的初值进行修正,经过多次循环迭代,即可得到目标三维位置和速度的融合结果[9]。
(6)
为保证方程的冗余性,一般需要3个以上测速设备的测量值有效,同时为了保证解算的实时性,参与融合的径向速度测元不宜过多。
2 实时数据融合仿真与分析
2.1 仿真条件
假定利用多部测试设备进行组网测试,测试数据可实时汇总参与融合处理。各参试设备标定准确,没有系统误差;弹丸飞行轨迹以某型导弹理论弹道为真值;各测试设备的距离测量值叠加10 m的随机误差,角度测量值叠加1 mrad的随机误差,将带有误差的直接测量值转换为弹丸的位置信息,以初步滤波融合后的弹丸位置信息为原始位置数据;各测试设备径向速度测量误差设定为0.1 m/s;3部测速设备布站方案及弹道轨迹如图1所示。
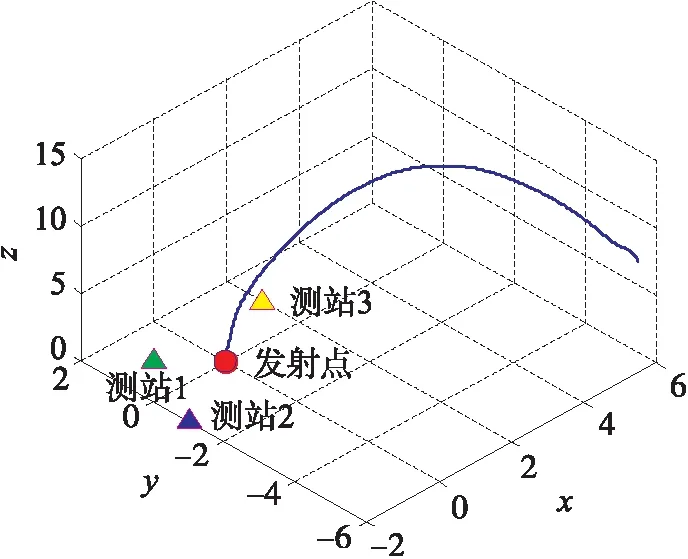
图1 弹丸飞行轨迹及测速设备布站示意图
所有测量数据经过初步滤波和初步融合处理后,得到弹丸实时三维位置信息和实时三维速度信息,作为后续处理的初值,其中三维位置信息精度较高,三维速度是由Kalman滤波的状态方程获得,其实质是位置差分计算得出的,从而导致实时三维速度信息精度较低[6]。实时三维速度解算结果相对于理论真值的误差曲线如图2所示,vx,vy,vz分别为3个维度上的速度。
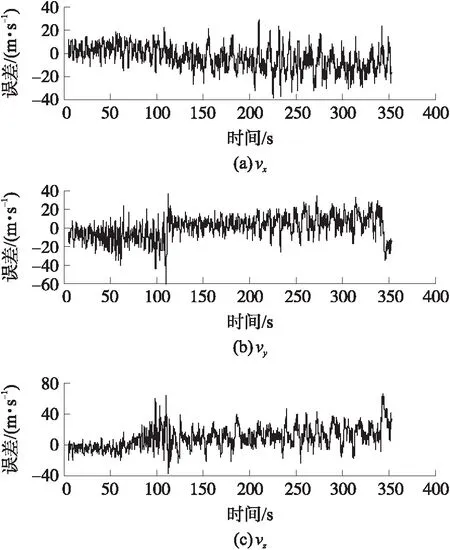
图2 原始三维速度误差曲线
在65 s和110 s左右,弹丸加速度发生变化时,原有处理方法对其不敏感,导致误差曲线突变;同时,还可以看出原有处理方法得出的随机误差很大,而且伴有一定的系统误差。
在上述数据基础上,分别应用直接IMM卡尔曼滤波、增加观测量的IMM卡尔曼滤波和融合处理方法对模拟常规靶场典型试验的测量数据进行实时处理仿真,并进行对比分析,其中2种IMM算法都采用匀速、慢加速和快加速3种模型[10]。
2.2 比较分析
应用IMM卡尔曼滤波[11-12]直接对原始三维速度进行滤波,以下简称IMM-1方法,滤波后的三维速度误差曲线如图3所示。

图3 IMM-1方法得到的三维速度误差曲线
经过多次参数调整,滤波后速度误差方差仍然没有降低,而且在65 s和110 s左右加速度突变时,滤波模型切换会有一定延迟,导致误差较大[13]。
不增加新的观测量,单纯通过改变处理方法,已经很难提高弹丸的实时三维速度精度,为此,增加径向速度作为观测量参与计算。经过线性化处理[14],弹丸的径向速度可与弹丸位置联立进行卡尔曼滤波。经验证,只增加1个或2个径向速度,对三维速度约束能力有限,给结果带来较大的偏差,滤波效果不理想。增加3个径向速度作为观测量再进行IMM卡尔曼滤波,以下简称IMM-2方法,滤波结果的误差曲线如图4所示。

图4 IMM-2方法得到的三维速度误差曲线
滤波后三维速度误差明显减小,但是处理结果存在一定的系统误差,同样在加速度突变时,滤波模型切换还是有一定延迟,导致误差增大。在初始时刻,测试设备与目标形成的空间几何关系较差,而且给定初值并不准确,滤波收敛需要一定的时间,这就导致初始三维速度误差相对较大。
加入3个径向速度作为观测量后,即达到了本文提出的融合处理方法的最低冗余要求,应用融合处理方法得到实时三维速度,其误差曲线如图5所示。
由图5可知,三维速度误差均方差明显降低,且均值趋于0,效果较好。经过对比,不难发现融合处理方法和IMM-2方法计算精度相近,但是IMM-2方法仍然有明显的系统误差残留,系统误差消除效果较弱,因此,应采用融合处理方法实时处理弹丸主动段三维速度。

图5 实时融合得到的三维速度误差
针对测控网络安控系统输入需求,重点关注弹丸主动段三维速度信息。弹丸主动段三维速度处理结果误差曲线如图6所示。

图6 融合求速得到的三维速度误差
在弹丸发射后,由于弹丸高度较低,与测站形成的几何关系较差,导致弹丸垂直方向的速度误差稍大,但是三维速度误差均在1m/s左右,已经达到安控系统的需求。
将上述方法得到的三维速度误差曲线进行统计,得到结果如表1所示。

表1 三维速度误差统计表
对比统计结果可以得出,利用融合处理方法和IMM-2方法都能够有效地实时计算弹丸三维速度,精度提高超过80%,而IMM-1方法无法进一步精确计算弹丸三维速度;从系统误差和合速度误差的角度,融合处理方法优于IMM-2方法;IMM-1方法和IMM-2方法处理结果都和未处理数据一样,含有一定的系统误差,而融合处理方法处理结果的系统误差很小。
3 结束语
基于以上的对比分析,可以得到如下结论:
①融合处理方法能够充分有效利用观测数据,提高了实时三维速度处理精度,且实时性强,易于工程实现;
②融合处理方法和IMM卡尔曼滤波都可以用来减小数据的随机误差,但是融合处理方法在减小系统误差能力上具有一定的优势;
③IMM卡尔曼滤波虽然对弹丸运动模型变化具有一定的自适应,但是模型切换会有一定的延迟,因此,卡尔曼滤波在处理突变数据时,效果并不理想;
④含有误差的位置信息对速度信息约束能力较差,而速度测量原理使径向速度测量精度较高,因此,在解算弹丸速度信息时,可以考虑将直接测量得到的径向速度用于数据处理。

