固定鸭舵双旋火箭弹弹体绕流的数值研究

冯 斌,于纪言,王晓鸣,王 钰

(南京理工大学 智能弹药技术国防重点学科实验室,江苏 南京 210094)

精确制导组件是一种拥有固定舵偏角,通过旋转通道与弹体解耦实现自发电和弹道修正的低成本弹道修正组件[1-2],因此有这种布局的弹丸也叫双旋弹。由于可以通过传统旋转弹药加装组件实现无控到有控的飞跃,因此精确制导组件技术是低成本有控弹药技术的主要发展方向。精确制导组件的气动外形[3-4]通常包括了一对同向偏转的差动舵和一对反向偏转的操纵舵,差动舵用于维持组件的转动,操纵舵则来产生气动修正力。

对于加装了修正组件的传统弹药,其气动外形发生了改变,在传统的旋转弹的基础上加入了鸭舵,因此其气动特性发生了改变。鸭舵对于弹体外流场的影响直接关系到弹丸外弹道飞行的稳定性及修正能力。目前对于双旋弹的气动特性研究主要分为全弹气动特性研究和关键部件设计两类。对于全弹整体的研究,程杰等[5]利用数值计算研究了双旋弹气动外形的改变对于弹道射程的影响;钱龙[6]、徐辉雯等[7]利用数值计算研究了全弹进动时的气动特性;潘雷等[8]研究了迫弹加装修正组件的气动特性。对于部件的设计,汪亚利等[9]利用数值计算研究了鸭舵的高度和舵偏角对于全弹气动力的影响;沈皓敏等[10]利用数值计算研究了双旋迫弹的翼型参数对于稳定储备量的影响;刘琦等[11]同样使用数值计算研究了双旋迫弹的舵偏角的影响。

目前对于双旋弹的研究缺少对于鸭舵-弹体干扰的影响,尤其是鸭舵产生的涡系对于弹体的影响。本文将对某加装精确制导组件的旋转稳定火箭弹外流场进行数值计算,并对鸭舵涡系进行辨识,定性分析其外流场,并对其受力进行定量对比。

1 数值方法

1.1 方法介绍

本文数值计算采用有限体积法(FVM)。选择弹身周围的空气域生成计算域,为了减少弹丸附近的扰动对于远场边界的影响,空气域的尺寸选择100倍特征长度。

本文使用圆柱形的计算域,圆柱的2个端面分别距离弹头和弹尾10.7 m,直径为10.7 m,同时适用于亚音速、跨音速和超音速工况,图1为计算域示意图。

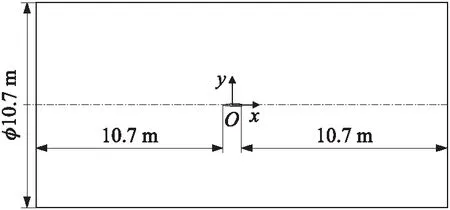
图1 计算域示意图

与此同时建立弹体坐标系,原点位于全弹的质心,x轴与弹轴重合指向弹尾,y轴垂直于弹轴指向上方,z轴与x轴和y轴符合右手关系。本文使用的是固定模型,修正组件的操纵舵位于水平面内,修正力指向y轴方向,即为飞行试验中起控的状态。

将所选取的空气域离散为海量的六面体网格,整体采用“O-C”型拓扑,如图2(a)所示。图2(b)为对称面上在弹体附近处的截面网格,为了对边界层流动进行精确捕获,需要对刚体壁面附近的网格进行加密。目前大量的研究均使用无量纲数y+来描述壁面网格的厚度,其定义为

图2 计算域网格

(1)

式中:uf为近壁面摩擦速度,y为第一层网格的厚度,ν为流体的运动黏度。根据本文选择的相关算法,需要保持y+≤1或30≤y+≤300,本文选取壁面网格高度2×10-6。

为了描述流体运动,配合本文采用的有限体积法,本文使用积分形式的纳维-斯托克斯方程作为控制方程组。对于对流项等空间导数均采用二阶迎风格式,根据前期的相关研究,更高阶的离散格式对于本文研究内容并没有明显的影响。考虑到超音速流场中存在间断的问题,本文采用Roe矢通量分裂格式构造网格面处的通量。对于湍流流动,本文选取雷诺平均方法,为了使方程组封闭,使用单方程的Spalart-Allmaras(S-A)湍流模型。本文使用了全隐式密度基求解器求解控制方程组,隐式方法允许采用更大的库朗数,有利于加速迭代的收敛。

使用无反射压力远场作为来流边界,马赫数1.2,温度300 K,静压101 325 Pa,弹体使用绝热无滑移壁面条件。

1.2 网格密度的研究

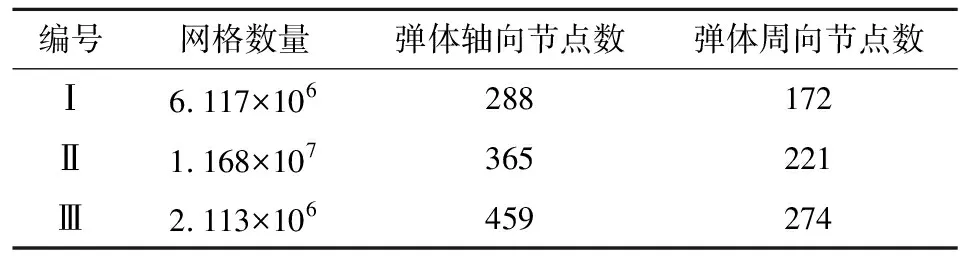
表1 网格主要节点参数

使用上节中提到的算法,在零攻角、马赫数1.2的工况下,分别利用3套网格计算得到流场。图3所示为阻力系数对比图,横轴为计算域网格总数的立方根。从图中看到3套网格得到的阻力系数差异不大,网格Ⅰ的阻力最小,网格Ⅱ的阻力最大,相对误差约为4.24‰。

图3 阻力系数对比图

为了研究网格密度对于鸭舵涡系捕获能力的影响,首先使用Q准则(见公式(2)),对流场中的涡旋进行辨识。根据Q准则,认为Q>0的区域为涡的核心区域。绘制Q=0的等值面图,可以观察到鸭舵尾涡的核心区域,如图4所示。从图中可以明显地观察到,舵片的翼尖涡自舵片附近产生,一直延伸到下游流场,在弹体表面也可以观察到卷起的边界层。

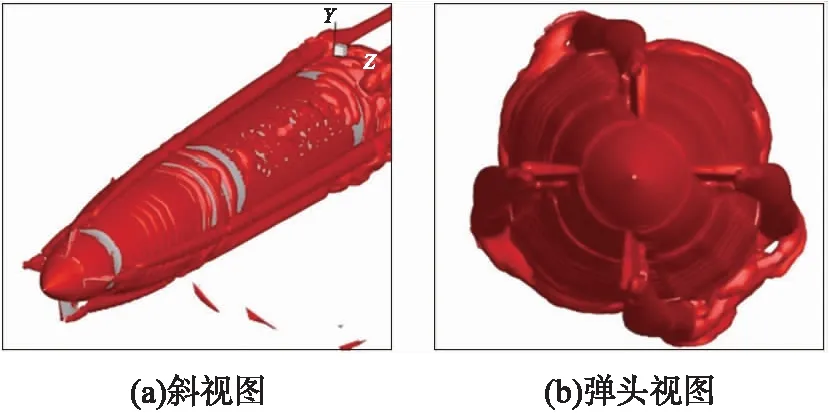
图4 Q=0等值面图

(2)

涡在流场中由于黏性的作用,涡量的强度会逐渐衰减,涡的动量耗散影响周围的区域,其直径会随着流动变大。在数值计算的过程中,将物理空间离散化后会产生不可避免的数值误差。经过数值试验,越稀疏的网格,涡耗散的速度越快,下游流场的涡核直径迅速变大;但是对于过于细密的网格,数值计算结果中的网格累积误差会越来越大,同时消耗巨大的计算资源,因此本文用涡核直径来量化网格质量。

由于弹尾的流动混乱使得翼尖涡不便观察,本文选取距离弹底0.1 m处的截面涡核直径进行研究。图5所示为3种不同密度的网格在该截面处的涡核位置,左侧图为4个涡核的分布,右侧图为顶部的涡核,并统计该涡核的直径。

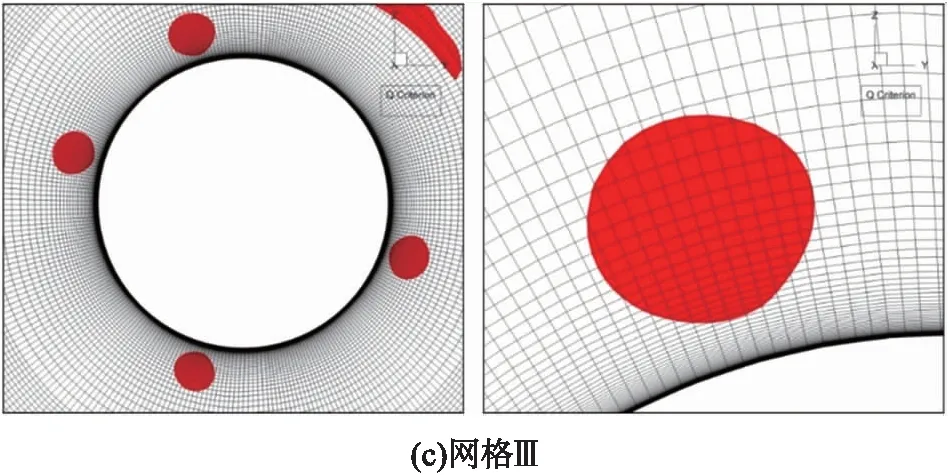
图5 距弹底0.1 m截面处弹体附近涡核

3种网格的顶部涡核里,网格单元数量分别为50,79和143,统计得到的涡核直径d见图6。网格Ⅱ的涡核直径小于网格Ⅰ,但是更细密的网格Ⅲ的涡核直径大于网格Ⅱ的,这印证了前文所提到的数值误差。综合考虑,选择网格Ⅱ作为本文研究所采用的计算网格。

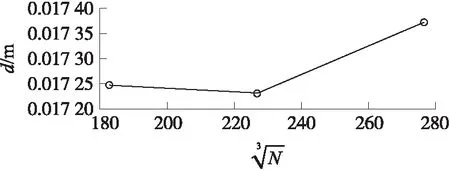
图6 3套网格涡核直径对比

2 流场定性分析

2.1 典型弹体流场分析

由于加装修正组件,回转体弹体受到修正组件的影响,尤其是斜置鸭舵产生的涡系的影响,本节将分析一种典型的双旋弹弹体附近的流场,以零攻角且1.2马赫数的工况下计算得到的流场结果为例。

首先研究弹体表面的压力系数,压力系数定义为

(3)

由于鸭舵涡系分为4个主要的涡,因此绘制4个方向弹体的压力系数云图,如图7所示。

图7 弹体表面压力系数云图

可以观察到弹体上条带状的低压区域,趋势线在图中用虚线绘制出。图中的带状区域分布位置与鸭舵涡系扫过弹体的区域基本一致。定量对比弹体的受力情况,弹体轴向力增大了1%,与此同时,由于涡系的非对称分布,弹体也出现了侧向力,将在第3节讨论。

2.2 弹体旋转运动对流场的影响

作为旋转稳定弹,该弹在飞行过程中弹体高速旋转,带动周围气流转动,鸭舵产生的涡系受到其影响。分别绘制零攻角且1.2马赫数下,距离弹底0.1 m处截面上的涡核以及流线图(弹头视角),如图8所示。弹体的转动角速度ω分别为0,100 s-1,200 s-1和300 s-1。

图8 零攻角下距弹体0.1 m截面处弹体附近涡核及流线图

从图8中可以观察到,随着弹体转速的增大,鸭舵涡系发生了偏转。该截面上涡核的位置出现了逆时针方向的移动(与弹体转动同向),且弹体转速越高,这种现象越明显,偏转的角度越大。值得注意的是,由于弹体的旋转与右侧舵片尾涡的方向相同,在右侧出现了一个诱导产生的涡,其产生机理如图9所示。其余3个舵片的尾涡方向与弹体相反,因此未出现这种情况。

图9 诱导涡产生机理

2.3 弹体攻角对流场的影响

当出现攻角时,弹体除了受到轴向来流的影响,还受到横向气流的作用。继续以距离弹底0.1 m处的截面为例,首先对比弹体零转速的情况,8°攻角的涡核及流线图,如图10所示。与零攻角的情况不同,8°攻角的鸭舵尾涡主要集中在背风侧,迎风侧的涡过于靠近弹体的附面层,在后者的作用下,涡更快地耗散掉了。在背风侧的涡系可以观察到3个主要的鸭舵产生的涡以及一系列诱导产生的次级涡。即使在弹体没有旋转的情况下,流场也呈现出非对称特性。

图10 8°攻角下距弹体0.1 m截面处弹体附近涡核及流线图

在8°攻角的情况下,弹体出现转动时,鸭舵产生的3个涡依旧分布在背风侧,随着弹体转速的提高,左侧的涡更靠近弹体,右侧的涡远离弹体。最靠近弹体的诱导涡向弹体旋转方向发生了更明显的扭转。

3 弹体受力分析

3.1 零攻角弹体受力

在零攻角的情况下,弹体的法向力系数Cy和侧向力系数Cz随弹体转速的变化如图11所示。

图11 零攻角下弹体法向力系数及侧向力系数随弹体转速变化曲线

随着弹体转速增大,法向力系数和侧向力系数的幅值也逐渐变大。弹体受到的垂直于弹轴的合力系数幅值变化如图12所示,弹体转速越高,弹体受到的垂直于弹轴的合力越大。

图12 弹体法向合力系数随弹体转速的变化

为了确定弹体侧向力和法向力出现差异的原因,绘制弹体转速为0和300 s-1条件下,距弹底0.1 m处截面上的压力系数Cp,如图13所示(弹头视角)。

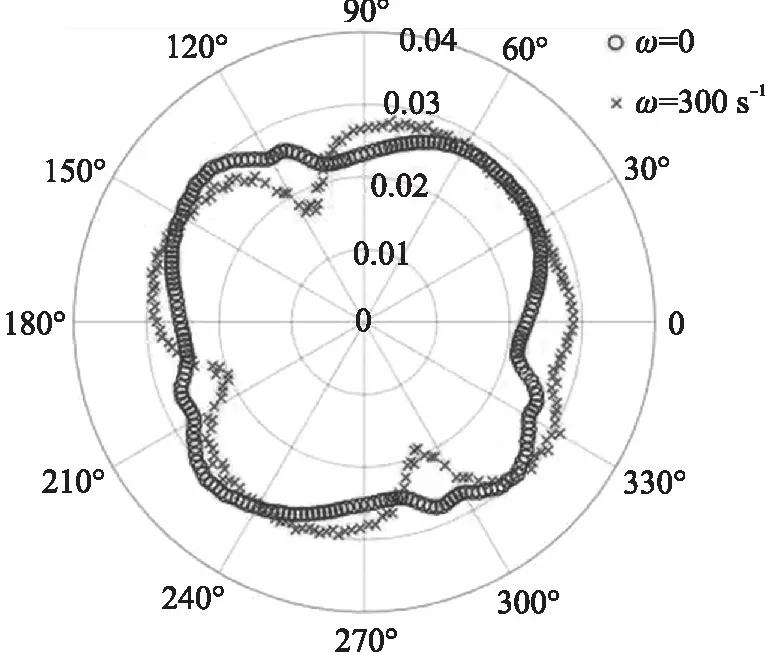
图13 零攻角下弹体截面压力系数Cp(弹头视角)

弹体静止时,弹体表面存在4个低压区域,位置与鸭舵涡系扫过弹体的部分重合。当弹体以300 s-1转动时,低压区域向弹体旋转方向发生了偏转。同时,3个低压区的压力系数明显减小,1个低压区的压力系数上升,这与涡的旋转方向和弹体旋转方向有关,示意图见图14(弹头视角)。

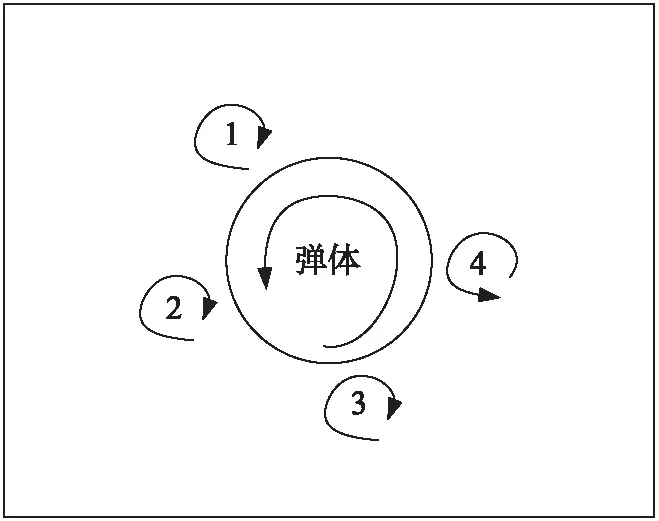
图14 涡系与弹体旋转方向示意图

图14中1号、2号、3号涡的影响受到弹体旋转而加强,4号涡的影响受到弹体旋转而减弱,弹体表面压力分布的非对称性明显加强,这解释了零攻角时弹体旋转导致弹体侧向力变大的原因。

3.2 多攻角弹体受力

对比攻角分别为0,4°,8°时的弹体法向力系数和侧向力系数,如图15所示。

弹体法向力系数见图15(a),其幅度随弹体转速的提高而增大,且呈现非线性,转速越高,法向力增大得越快。当攻角增大时,弹体法向力系数明显增大,且受弹体转动影响越大。

弹体侧向力系数见图15(b),弹体的马格努斯效应十分明显,与弹体的转速和攻角均成正相关。与传统回转体弹丸不同的是弹体转速为0时的侧向力系数不为0,且与攻角相关。

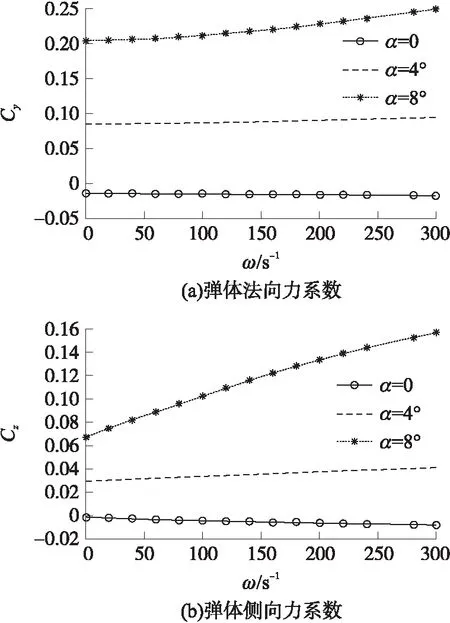
图15 不同攻角下弹体法向力系数及侧向力系数随弹体转速变化曲线

与前节相同,对比8°攻角下,弹体转速为0和300 s-1条件下,距弹底0.1 m处弹体截面上的压力系数,如图16所示(弹头视角)。

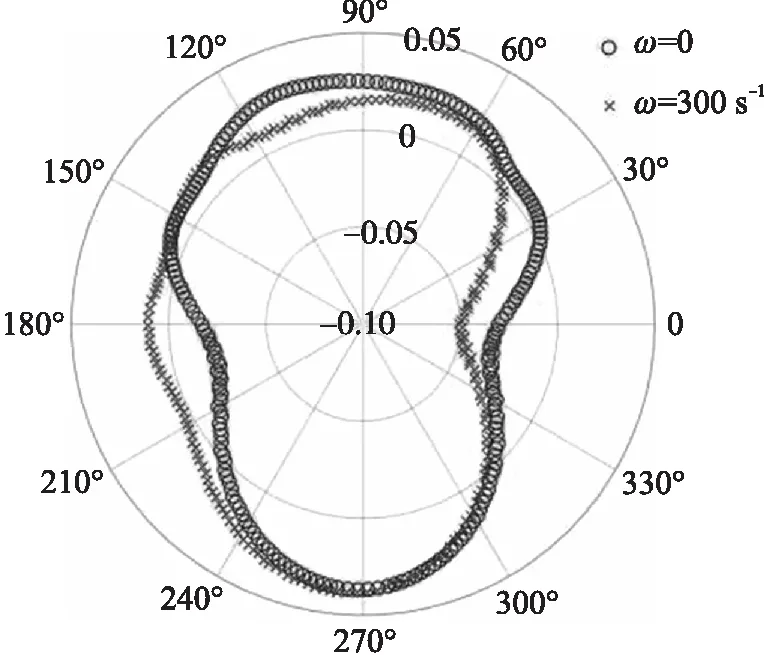
图16 8°攻角下弹体截面压力系数Cp(弹头视角)

弹体在静止时,弹体压力系数的非对称主要由于背风侧的涡系影响所致,弹体转动后,非对称压力分布更加明显,这与弹体侧向力随转速增大的现象吻合。

4 结束语

本文利用计算流体力学方法对某双旋修正火箭弹的外流场进行了数值计算,重点研究了鸭舵的存在对于弹体受力的影响。首先,讨论了网格密度对于数值计算的影响,尤其是对于鸭舵尾涡辨识的影响。选择合适密度的计算域网格,对1.2马赫数多攻角多转速工况的双旋弹流场进行了计算。得到如下结论:

①鸭舵涡系会使弹体上出现条带状低压区域,不对称的涡系使弹体受力不再对称;

②鸭舵涡系会由于弹体的转动而发生扭转,其扭转方向与弹体转动方向一致,因此,弹体的法向力和侧向力均受到影响;

③鸭舵涡系与弹体旋转共同作用下,诱导产生次级涡。

④存在攻角时弹体的侧向力仍然表现出明显的马格努斯效应。与传统回转体弹丸不同的是弹体转速为0时的侧向力系数不为0,且与攻角相关。

高旋弹的飞行稳定性与其马格努斯力矩息息相关,双旋结构的弹丸侧向力和偏航力矩同时受到弹体转动和鸭舵涡系的影响,这种非线性耦合关系的研究对于外弹道稳定性分析和修正组件设计有重要意义。

未来的工作将着重于组件的不同角度、不同转速对弹体乃至全弹气动力的影响,完成相关的模型建立。