基于北斗导航的机器人弹道曲线航道导航系统

李 峰,岳 云,张跃进,张雪松,朱文慧

(1.郑州经贸学院 智慧制造学院,河南 郑州 450007;2.郑州宇通集团有限公司,河南 郑州 450007;3.郑州经贸学院 公共教学部,河南 郑州 450007;4.中原工学院 机电学院,河南 郑州 450007)

现在战争的主要武器之一是导弹,对导弹的导航、控制,主要是通过对其弹道曲线进行控制。弹道曲线是抛物体在空中飞行过程中所经过的轨迹、路径。在理想的情况下,可以用弹道曲线控制各种飞行器的有效运动和打击范围。通过控制弹道曲线,有效保证弹头落点的密集度、空间的有效性,使导弹准确可靠地完成空中飞行动作,飞抵最终目标。因此,在飞行器控制领域,弹道曲线研究是目前的研究热点。相关研究者通过弹道曲线研究深入分析了机动弹道及制导方法,为将弹道曲线应用于飞行器控制打下了良好基础[1-5]。

随着科技的发展,机器人也越来越成为战争的主要武器。美国的机器人战士”Atlas”,日本的机器人士兵“机动战士”,俄罗斯的军用仿人机器人“FEDOR”都已具备一定的实战能力[6-8]。很多国家现在在机器人士兵方面投入了大量的人力、物力和财力,机器人导航控制也越来越成为研究的重点。文献[9-13]以不同方法和媒介研究了机器人的导航控制,但将弹道曲线应用于机器人,特别是人形机器人的导航控制尚是空白,而将比较成熟的弹道曲线控制应用于机器人控制,提高机器人的智能化程度,优势非常明显。一般人形机器人到达预定区域主要通过激光、地磁、地图等方法导航,多以直线航道方式,行动方式比较单一,而人形机器人要成功到达预定区域完成任务,并成功保护自己,躲避敌方打击,就需要以不同的航道和导航方式来实现,因此要提高人形机器人导航的智能化程度。本文以人形机器人弹道曲线航道导航为研究重点,通过北斗系统国家2000坐标下机器人导航实验,成功地实现了人形机器人的弹道曲线航道导航控制,极大地提高了人形机器人导航控制的智能化程度。

1 人形机器人弹道曲线航道北斗导航模型

1.1 人形机器人运动学模型

图1为机器人运动学模型。与人形机器人双足中心连线垂直的中心线为yr,大地的正北方向为y。人形机器人运动时,双足与纵轴yr之间α为机器人转向角,机器人坐标系中yr轴与大地坐标系y轴之间的夹角ψ为机器人现在所处位置的姿态角。图中,O0(x0,y0)为人形机器人初始坐标,Ot(xt,yt)为终点坐标,O0Ot与y之间的夹角ψh为人形机器人此位置的航向角。

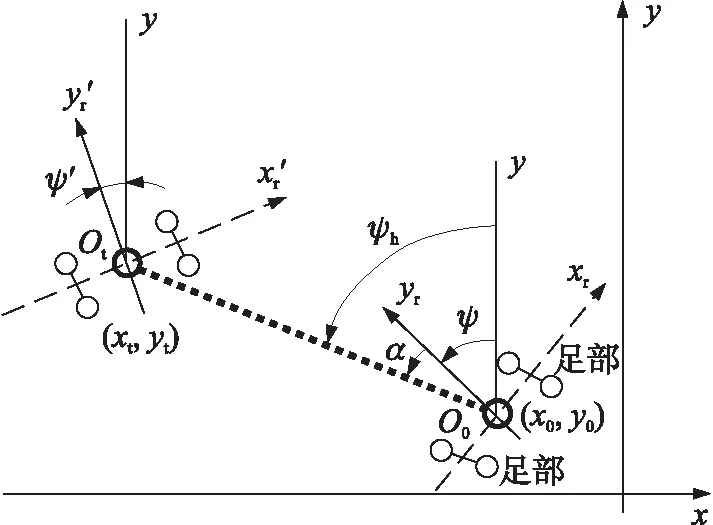
图1 机器人运动学模型

如果机器人达到(xt,yt)处后有姿态ψ′要求,机器人到达目的地后还需要进行姿态调整。O0与Ot两点距离为s,如果人形机器人行进速度为v,转动角速度为ω,则有:

ψh=-arctan((xt-x0)/(yt-y0))

(1)

式中:

yt=y0+scosψh=y0+vΔtcosψh

(2)

xt=x0+ssinψh=x0+vΔtsinψh

(3)

ψh=ψ+α=ψ+ωΔt

(4)

1.2 弹道曲线航道模型

图2为人形机器人弹道曲线航道变换模型。图2中曲线1为普通弹道曲线,从图中可以看出成抛物线样式,左右对称。但机器人遇到特殊环境和突发情况时,人形机器人若需从所在点到任务目标点确定一条基于弹道曲线的航道,安全完成任务,则需对特定曲线1进行变换。如图2,可通过将弹道曲线先旋转,后平移,将曲线1旋转为曲线2,后移动至曲线3,使曲线3通过所在位置和终点位置。机器人弹道曲线航道及导航模型参数的确定需要大量的计算,具体见人形机器人弹道曲线航道北斗导航算法设计。

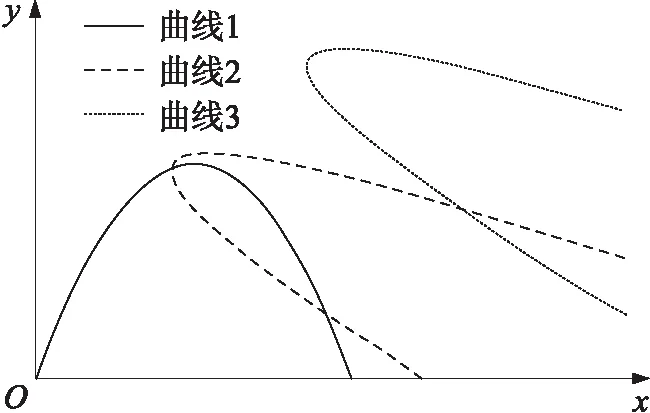
图2 人形机器人弹道曲线航道变换模型

1.3 人形机器人弹道曲线航道北斗导航模型

图3 人形机器人弹道曲线航道北斗导航模型

(5)

式中:nl(i)为第i段内可继续差分nl(i)次,每次位移Δl。

从第i-1段到第i段需进行航向调整,人形机器人转向角为

Δα(i)=nα(i)Δθ

(6)

式中:nα(i)表示第i段转向角可继续差分nα(i)次,每次Δθ。

2 人形机器人弹道曲线航道北斗导航算法设计

2.1 人形机器人弹道曲线方程确定

弹道曲线参数方程为

(7)

式中:vr,ξ为参数项;g为常数项;t(i)为自变量。则图2中曲线1所示人形机器人弹道曲线方程为

(8)

令:

(9)

2.2 初始条件

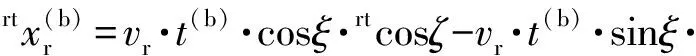
(10)

(11)

rtx(n)=vr·t(n)·cosξ·rtcosζ-vr·t(n)·sinξ·
rtsinζ+[g·(t(n))2·rtsinζ/2]+rtχ

(12)

(13)

2.3 关键参数确定

(14)

所以:

(15)

则有:

(16)

因此:

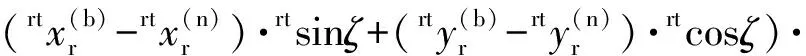
(17)

(18)

将式(17)和式(18)代入式(10)和式(11):

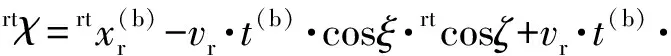
(19)

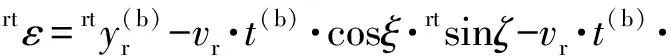
(20)

弹道曲线N点差分,则:

t(i)=t(b)+i·[(t(n)-t(b))/(N-1)]

(21)

rtx(i)=vr·t(i)·cosξ·rtcosζ-vr·t(i)·sinξ·
rtsinζ+[(g·(t(i))2·rtsinζ)/2]+rtχ

(22)

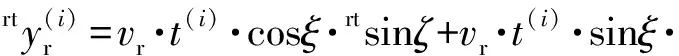
(23)

式中:i=1,2,…,N-1。

结合式(1)～式(6),可完成人形机器人弹道曲线航道规划过程。

3 系统组成与工作原理

根据图4导航系统整体架构,人形机器人弹道曲线航道北斗导航系统主要由被导航人形机器人、弹道曲线航道规划模块、人形机器人位姿规划模块、CPU、控制柜、中间控制器等部分组成。通过北斗导航器得到人形机器人所在地国家2000坐标,通过弹道曲线航道规划模块完成弹道曲线设定,通过人形机器人位姿规划模块规划人形机器人弹道曲线航道中各点位姿,通过控制柜、中间控制器及相关辅助设备具体完成人形机器人弹道曲线航道任务。

图4 人形机器人弹道曲线航道北斗导航系统整体架构

系统在确定机器人所在坐标及目的坐标后,通过弹道曲线航道规划模块自动规划生成弹道曲线,与普通机器人导航系统不同,该导航系统生成点对点的弹道曲线运动轨迹,而非点对点的直线运动轨迹,因此,智能程度更高。在得到弹道曲线后,由人形机器人位姿规划模块规划弹道曲线航道人形机器人位姿变化,然后通过控制柜、中间控制器等设备向人形机器人发出动作指令,控制人形机器人按照人形机器人位姿规划动作,沿弹道曲线到达目标位置,完成任务。

4 人形机器人弹道曲线控制过程设计

4.1 控制过程设计

图5为人形机器人弹道曲线航道北斗导航控制系统流程图。

图5 人形机器人弹道曲线航道北斗导航控制系统流程图

按照图5,将系统初始化后,系统按照人形机器人弹道曲线航道北斗导航算法设计解算弹道曲线主要参数,并生成弹道曲线。弹道曲线生成后,系统结合图1人形机器人运动学模型和图3人形机器人弹道曲线航道北斗导航模型规划人形机器人动作航道和姿态。接着,人形机器人按照规划从第1坐标点(初始位置)调整姿态,确定1到2点(第1段)航向,运动,到达第2点后系统内部参数更新,继续按照规划在第2坐标点调整姿态,确定2到3点(第2段)航向,运动……直到系统到达终点N,系统校核位置,自适应调整位姿。系统通过差分弹道曲线,自动规划人形机器人动作,实现人形机器人弹道曲线航道北斗导航,智能化水平高,自适应能力强。

4.2 主要运动控制原理

根据控制流程,结合导航模型,采用stl语言将人形机器人弹道曲线导航模型及导航算法程序化,主要控制原理见图6和图7。从图6弹道曲线规划过程可以看出,控制系统在输入弹道曲线相关参数后,按照人形机器人弹道曲线航道北斗导航算法,对经过初始点、终点的弹道曲线进行结算,并调用相关子程序,自动生成弹道曲线。

图6 弹道曲线规划过程

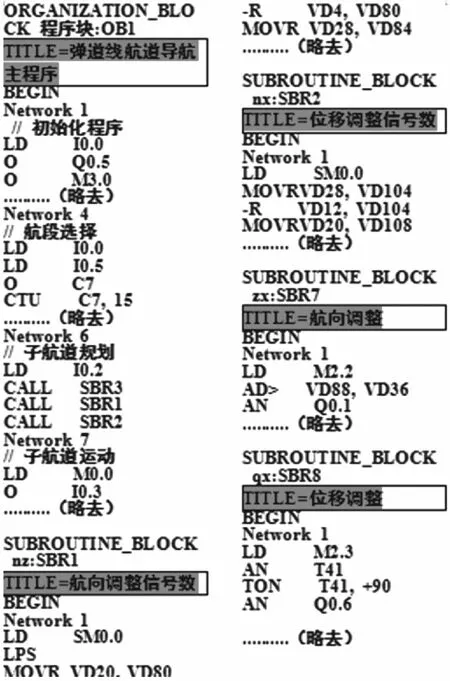
图7 人形机器人弹道曲线航道北斗导航主程序

图7为依据图5人形机器人弹道曲线航道北斗导航控制系统流程图而研发的人形机器人弹道曲线航道北斗导航主程序,因弹道曲线导航过程是一个复杂的过程,程序中略去了大量参数传送和动作程序。图6和图7结合图4人形机器人弹道曲线航道北斗导航系统,即可完成人形机器人弹道曲线航道北斗导航。

5 实验验证

5.1 实验参数

人形机器人弹道曲线航道北斗导航控制过程比较复杂,整个过程包括弹道计算、航道规划、任务实现等,通过实验一方面验证人形机器人弹道曲线航道北斗导航算法的正确性,另一方面验证系统的可行性。实验主要参数见表1。

表1 实验主要参数

5.2 仿真分析与实验研究

为了检验人形机器人弹道曲线航道北斗导航算法的合理性、正确性,根据表1参数,一方面利用METLAB软件对人形机器人弹道曲线航道北斗导航模型进行仿真,另一方面通过导航系统对模型进行实验验证,仿真及实验结果如图8和图9所示。图8中曲线4为弹道曲线仿真结果,曲线5为人形机器人弹道曲线导航航道仿真结果;图9中曲线6为人形机器人弹道曲线航道北斗导航实验结果。

图8 弹道曲线与导航航道仿真结果

图9 人形机器人弹道曲线航道北斗导航实验结果

图10为实验得到的导航轨迹与弹道曲线的误差图。

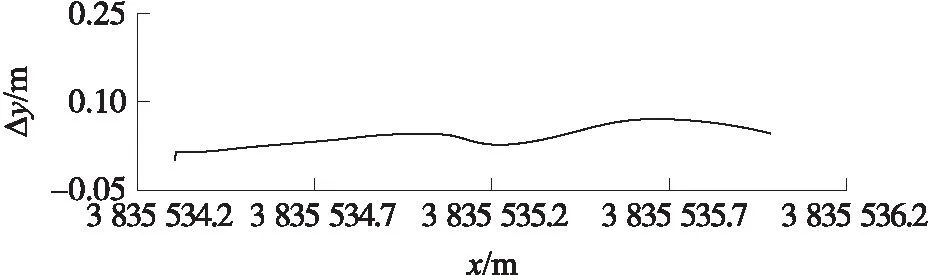
图10 弹道曲线航道导航位移误差图

图8中,曲线4弹道曲线和曲线5人形机器人弹道曲线航道接近,这说明导航算法达到了使人形机器人弹道曲线航道与弹道曲线接近的目的,可以实现人形机器人弹道曲线航道导航。在图9的导航实验结果中,曲线4也逼近曲线6,说明所设计的人形机器人弹道曲线航道导航系统是合理的,可以实现人形机器人弹道曲线航道导航目标。曲线4与曲线5之间的误差主要是因为人形机器人本身航向调整误差、位移调整误差积累的结果,人形机器人每信号调整角为10°,调整位移为0.05 m(见表1),导航控制信号越多,误差积累越大,后期可通过提高机器人本身的动作精度降低误差积累。曲线4与曲线6之间误差一方面是因为控制系统误差,另一方面导航轨迹各处摩擦系数不同,造成机器人在个别位置移动结果差别,从图10中可以看出导航轨迹与弹道曲线误差在-0.05～0.1之间,后期可以通过完善实验环境,提高人形机器人脚部摩擦系数等方法,进一步提高人形机器人导航效果。结合图8～图10可以看出,导航算法及导航系统可以实现人形机器人弹道曲线航道北斗导航,有效地提高人形机器人的智能化程度。

图11～图13所示为弹道曲线导航航道理想航向、仿真航向、实验航向、理想航向与实际航向误差。随着人形机器人的运动,人形机器人的航向需要随着航道及时变化,以满足机器人导航航道要求。

图11 弹道曲线理想航向与仿真航向变化曲线

图12 弹道曲线理想航向与实验航向变化曲线

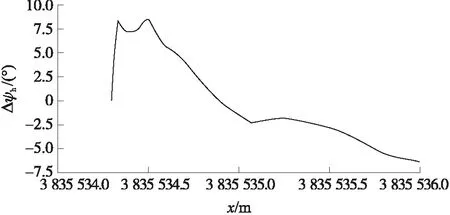
图13 弹道曲线航道导航航向误差图

理论上,人形机器人在整个导航过程中,其航向围绕理想航向上下波动,但波动范围在10°左右,这主要是由人形机器人本身因素造成,人形机器人每信号调整角为10°(见表1),此误差是不可避免的,后期可以通过提高机器人每信号调整精度,但精度提高又增加了计算量,增加了导航控制信号数,提高了控制难度,后期可以通过各种算法对此进行优化。从图13可以看出,航向误差也维持在10°内,在-7.5～8.5之间,部分区域因地面摩擦和规划航向变化有较大变化,但整体在误差范围内。结合图11～图13,再次验证了人形机器人弹道曲线航道北斗导航算法的正确性和导航系统的可行性。

6 结束语

将弹道曲线应用于人形机器人导航控制方面,建立了弹道曲线模型和人形机器人弹道曲线航道北斗导航模型,提出了人形机器人弹道曲线航道北斗导航算法。根据导航模型和算法,研发了一种人形机器人弹道曲线航道北斗导航系统,以stl语言为媒介,将人形机器人弹道曲线导航模型及导航算法程序化,介绍了机器人弹道曲线航道北斗导航控制原理。METLAB仿真分析和人形机器人弹道曲线航道北斗导航实验研究结果表明,人形机器人弹道曲线航道北斗导航算法和导航系统是合理有效的,这为提高人形机器人的智能化程度,增强人形机器人在特殊环境、突发情况下的自适应能力打下了良好基础。