某型弹道修正弹落点散布规律研究

宋谢恩,王伟鹏,丁 锋,尚春明

(中国人民解放军95927部队,河北 沧州 061000)

传统无控弹药射击过程中,影响射击精度的因素复杂多样,且多呈正态分布[1-2],这也就导致了无控弹落点近似服从二维正态分布[3]。无控弹的射击精度分析、毁伤效能评估[4]等均以此为基础。而弹道修正弹射击精度的影响因素不仅包括了无控弹的所有因素,还增加了修正控制这一因素[5],其落点散布是否仍服从正态分布,需要进一步分析。

与传统无控弹药类似,弹道修正弹的射击精度分析以及后续的作战使用等,都需要准确分析落点散布规律。修正弹的落点散布是否服从正态分布,服从怎样的正态分布,亟需分析论证。

为了确定修正弹的落点散布规律,本文通过蒙特卡洛仿真方法[6]模拟打靶,获得大量落点坐标数据,利用统计学的方法,对落点数据进行概率统计分析,给出修正弹的落点散布规律及其分布的概率密度函数。

1 射击精度数值仿真结果

某型弹道修正弹采用“阻力板+脉冲推冲器”进行弹道修正。修正策略是纵向上“瞄远打近”,主要利用阻力板进行修正,只有偏近时才用脉冲推冲器修远;横向修正完全由脉冲推冲器完成;弹道上升段主要进行横向修正,下降段进行综合修正[7]。

基于上述修正策略,建立弹道方程。

弹体质心运动在发射系内的动力学方程为

(1)

(2)

式中:ϑ为俯仰角,ψ为偏航角。

在准弹体坐标系内弹体围绕质心转动的动力学方程为

(3)

式中:J为转动惯量,ω为转动角速度,M为气动力矩,γ为弹体滚转角。

在发射坐标系内建立的火箭弹质心运动方程为

(4)

火箭弹在准弹体坐标系内的姿态角速度方程为

(5)

式(1)～式(5)组成弹体的6自由度弹道方程。

弹体无控飞行时受到的轴向气动力大小为

(6)

式中:ρ为空气密度,S为弹体参考面积,c为轴向力系数,弹道解算时需将轴向力转换到发射系。

设阻力板展开后轴向力系数变为c′,则阻力板展开后,有:

(7)

影响该型无控弹射击精度的主要因素可以分为弹体加工及组装偏差、气动偏差、气象偏差、初始扰动偏差、射击诸元误差等5类,各种误差共同作用造成了落点散布偏差。相应的引起弹道偏差的主要因素的数值见表1。表中,σ为相应参数的标准差。

表1 无控弹散布影响因素初值设置

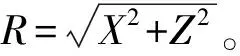
从10 000组数据中随机抽取1 000组,以瞄准点为原点,得无控弹和修正弹的落点散布如图1所示。从图1中可以看出,修正弹较无控弹射击精度有明显提高。由局部放大图2得出修正弹落点多数位于以目标点为中心的一个100 m×100 m的方框内。

图1 无控弹和修正弹落点散布对比图

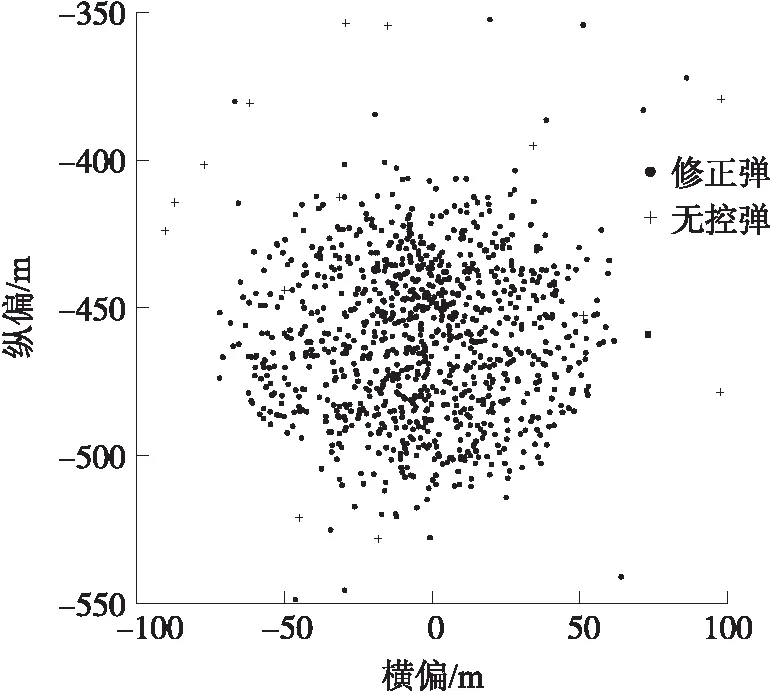
图2 落点散布局部放大图

2 落点散布规律研究

修正弹的落点散布规律可以通过分析仿真打靶数据得到。采用直方图法观察落点纵、横向误差和距离的大致分布,初步判断其分布规律并提出假设。之后通过概率纸验证法、P-P图法、单样本K-S检验、偏度峰度计算等方法分析具体规律,并最终求得落点散布概率密度函数。

2.1 描述性统计指标

首先对落点偏差数据进行基本的描述统计,结果如表2。无控弹的纵向、横向落点散布误差相关系数为0.014 7,修正弹的纵向、横向散布相关系数为0.042 6,可以认为2种弹的落点纵向、横向散布均是不相关的。

表2 落点散布数据描述统计表

由表1可以看出,修正弹的射击精度相比于无控弹有数量级上的提高。

2.2 直方图法

以仿真结果为样本,得到无控弹和修正弹的纵向偏差、横向偏差、距离偏差直方图如图3～图5所示。

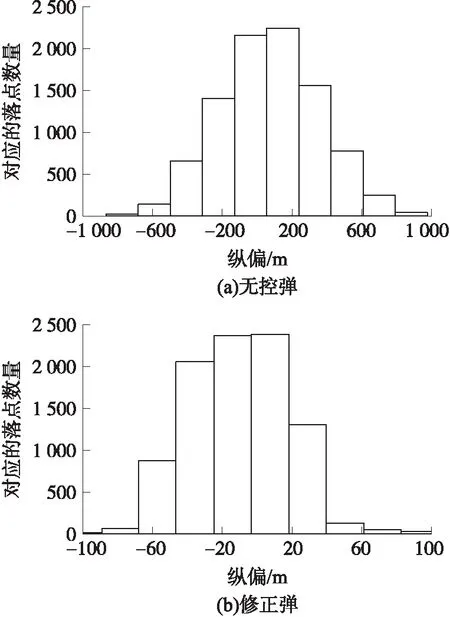
图3 纵向偏差直方图

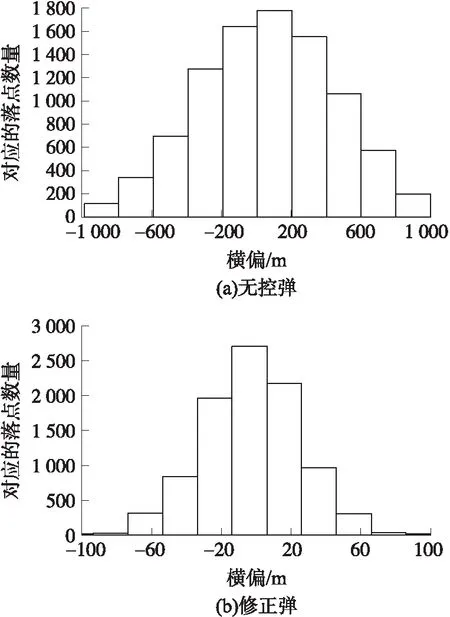
图4 横向偏差直方图

图5 距离偏差直方图

由图3(a)、图4(a)可以明显看出无控弹在纵向、横向散布上的正态性,图3(b)和图4(b)有一定的正态性,需要进一步检验。图5(a)和图5(b)分布不是很确定,需要其他方法来判定其分布规律。

2.3 概率纸法

采用概率纸检验法[8]检验各项散布参数的正态性。将样本值由小到大排列,依次画在正态概率纸上。凭直观画一条直线使其两边点数大致相等。如果各点(尤其是50%附近的点)离直线的偏差均较大,则认为样本变量不服从正态分布。无控弹和修正弹纵向偏差、横向偏差和距离偏差的正态概率纸检验结果如图6～图8所示。

由图6～图8可以看出,无控弹纵向偏差、修正弹横向偏差与正态分布最接近,其次是无控弹横向偏差、修正弹纵向偏差,无控弹距离偏差也与正态分布接近,但其有明显的不对称性,修正弹距离偏差与正态分布相差较大。

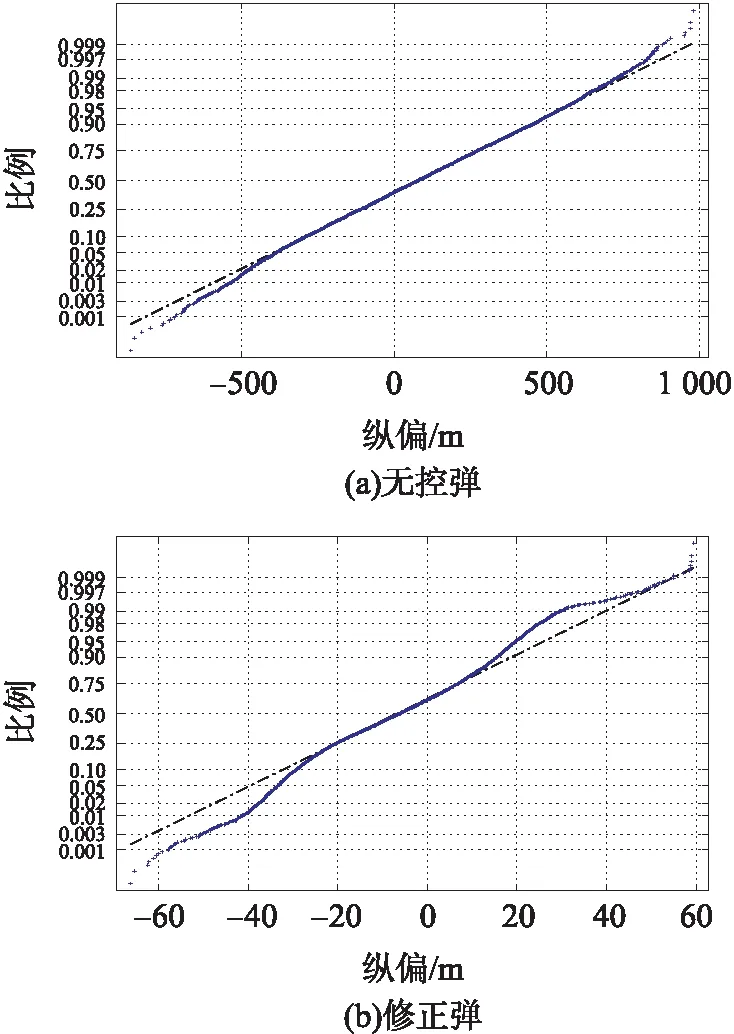
图6 纵向偏差概率纸检验

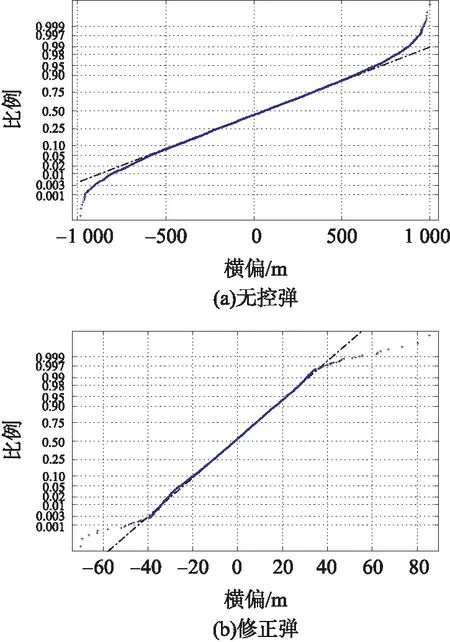
图7 横向偏差概率纸检验

图8 距离偏差概率纸检验

2.4 SPSS软件分析

为了量化各偏差与正态分布的接近程度,利用SPSS软件进行显著性水平为0.05的K-S检验,输出结果:无控弹、修正弹的距离偏差R的渐进显著性均为0,小于0.05,说明二者不服从正态分布,其他几项与正态分布较为接近,无控弹横向偏差、无控弹纵向偏差、修正弹横向偏差、修正弹纵向偏差的显著性依次为0.811,0.565,0.426,0.317。

之后利用SPSS软件画出无控弹、修正弹距离偏差散布对不同分布的P-P图,经过多次尝试,得出两者最接近韦伯分布,如图9和图10所示。

图9 无控弹距离偏差P-P图(韦伯分布)

图10 修正弹距离偏差P-P图(韦伯分布)

2.5 偏度、峰度法

正态检验最常用的方法是偏度、峰度法[9],下面以修正弹纵向偏差为例给出具体过程。零假设H0:修正弹纵向偏差服从正态分布。备择假设H1:没有理由相信修正弹纵向偏差服从正态分布。将修正弹的纵向偏差从-180～180 m以5 m为间隔共分为72组,求出组中值Xi和落入每组中的落点频率fi,i=1,2,…,72,数据总量n=10 000,如表3所示。

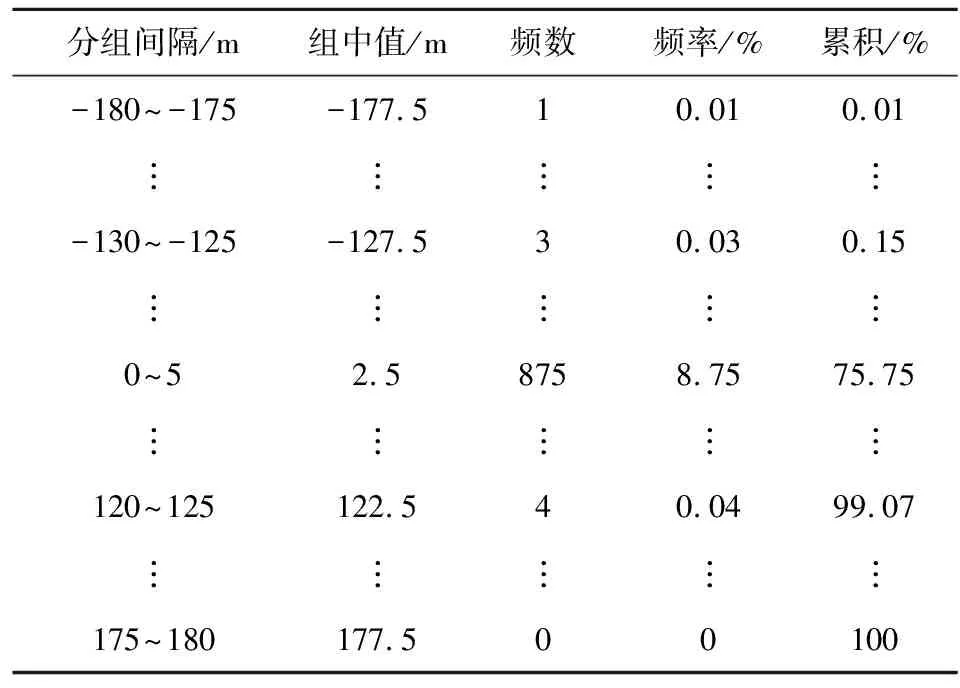
表3 修正弹纵向偏差统计表

(8)

计算样本偏度g1、峰度g2:

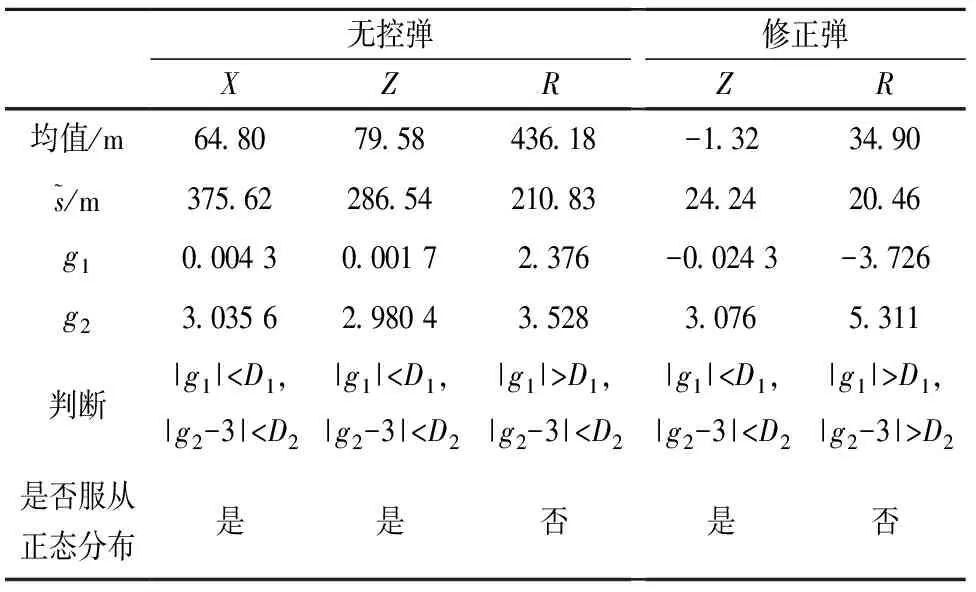
表4 偏差、峰度法正态性检验

2.6 Z标准化方法

为了得到各偏差量的具体概率密度函数,需要将原始数据标准化。采用:

(9)

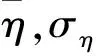
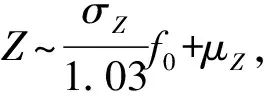
图11 修正弹横向偏差标准化概率密度曲线

对于判断为正态分布的其他几项偏差按照同样方法处理,得到标准化修正后的概率密度曲线如图12和图13所示,各自的概率密度函数为:无控弹纵向散布偏差X～N(80.2,266),修正弹纵向散布偏差X～N(-3.2,30.4),无控弹横向散布偏差Z～N(65.8,370)。

韦伯分布的概率密度函数为

(10)

式中:λ和k分别为标度、形状参数。

通过观察图12和图13可知,除了修正弹纵向偏差外,其他曲线与正态概率密度曲线很接近,这也验证了K-S检验中得出的渐进显著性结论。由图14可以看出,相对于正态分布,韦伯分布能准确描述射弹散布的距离误差,尤其是在距离误差较大的区域,其渐进显著性明显高于正态分布,所以判定其为韦伯分布,由于参数λ≈2,这样的韦伯分布也就是瑞利分布。

图12 横向偏差标准化改进概率密度曲线

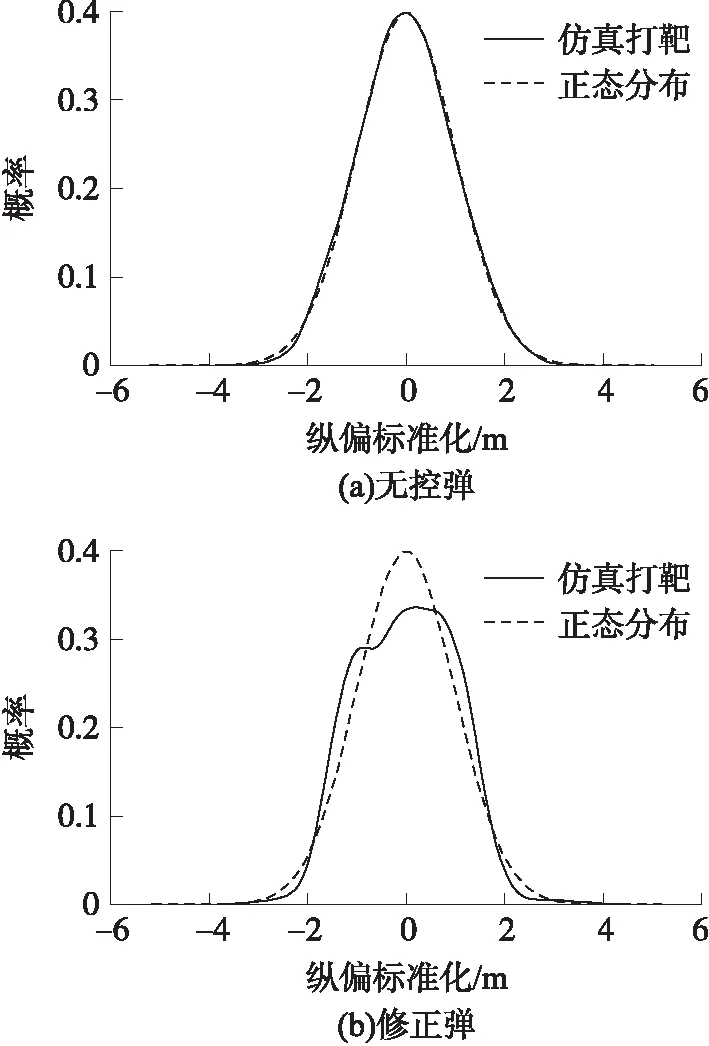
图13 纵向偏差标准化改进概率密度曲线

图14 距离偏差标准化改进概率密度曲线

3 射击精度计算结果

经过上述分析,基本确定该型弹道修正弹的落点散布与无控弹一致,都是二维正态分布。所以二者精度计算可以采用相同的指标和公式。圆概率误差δCEP、纵向散布误差EX、横向散布误差EZ作为常用的精度指标,存在近似的关系式[10]:

(11)

式(11)中炮兵常数为0.674 5。无控弹的射击精度指标还包括散布中心偏差和射击密集度等指标:散布中心偏差是指落点散布中心与瞄准点的偏差;射击密集度通常采用变差系数,即散布中间误差/射程求解。由落点数据可求得修正弹射击精度如表5所示。

表5 射击精度仿真结果对比

综合表2和表5可得,无控弹经过弹道修正后,纵向、横向散布中心偏差降低到原来的7.7%和2.0%,纵向、横向散布中间误差EX、EZ降低到原来的10.6%和6.9%,δCEP降低到原来的8.6%。修正弹除了射击精度较无控弹有明显提高之外,其纵向、横向散布比也发生了变化,从212.8/278.7=0.76变化为20.7/18.6=1.11,说明修正弹对横向(方向)的修正效果要好于对纵向(射程)的修正效果。

4 结束语

本文采用直方图法、概率纸法、偏度峰度法以及SPSS软件处理等,对某型弹道修正弹的落点散布规律进行了分析研究,最终得出修正弹落点纵向、横向偏差服从正态分布规律,落点距离偏差服从韦伯分布规律,可以采用与无控弹相同的射击精度评价指标和计算方法;利用Z标准化方法确立了修正弹落点纵向偏差、横向偏差、距离偏差的概率密度函数,为修正弹射击精度评估以及未来的作战使用和效能计算奠定了理论基础。