高维纵向数据的惩罚广义估计方程分析

尹长明，王亚东

(广西大学数学与信息科学学院，广西南宁530004)

1.引言

广义线性模型(GLMs)在研究响应变量是离散的或非负的回归问题中起着重要的作用[1].纵向数据(面板数据或集团数据)在生物医学，经济和社会科学的研究中经常出现.纵向数据是对一个个体的多次观测的数据是相关的，但相关程度未知，不同个体之间的观测数据是独立的.广义估计方程(GEE)[2]是常用的分析纵向数据下GLMs的方法[3]，GEE估计的一个显著特点是只要均值函数假定正确，即使相关阵(或协方差)假定不正确，得到的回归参数估计仍具有相合性和渐近正态性.若方差也假定正确，得到的估计方差最小.

高维协变量现在越来越普遍，特别是在基因研究和大规模健康研究中.例如酵母菌基因研究有96个协变量[4];心脏病的研究，协变量有年龄，抽烟情况，胆固醇含量，血压等等[5];有时变量虽然不多，考虑到各种交叉因素，协变量就很多.这些变量中有部分协变量与响应变量没有关系或者关系不密切，若将它们包含在模型中，会影响统计推断的精度，因此选择重要的协变量即变量选择就很重要.

关于GEE的大样本性质可参看文[5].当个体数n→∞，协变量维数pn可以趋于无穷时，WANG[5]在没有加稀疏条件下证明了GEE估计的大样本性质.变量选择的文献可参看文[6]，该文献假定协变量的维数pn是不变的，且响应变量是连续.WANG，ZHOU，QU[4]研究了响应变量可以是连续的，也可以是离散的(属性数据和计数数据)，协变量的维数pn可以是发散的纵向数据下广义线性模型的变量选择.本文改进了WANG，ZHOU，QU[4]和WANG[5]的结果.

设(Yij，Xij)是第i个个体的第j次观测值，i=1，2，···，n，j=1，2，···，m，其中Yij是响应变量，Xij是pn×1协变量，m是每个个体的观测次数.当个体数n→∞，协变量维数pn可以无界.假设不同个体之间的观测值是独立的，同一个个体的m次观测值是相关的.记Yi=(Yi1，···，Yim)T，Xi=(Xi1，···，Xim)，i=1，···，n，其中T表示矩阵或向量的转置.

设广义线性模型的期望和方差分别为

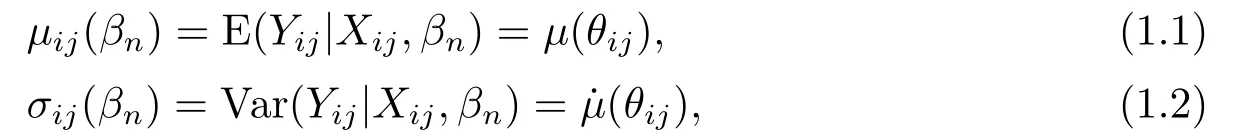
其中μ(θ)是联系(link)函数，˙μ(θ)＞0是它的导数，θij=XTijβn，βn=(βn1，···，βnpn)T是回归参数向量.当μ(θ)=θ，就得到线性模型;μ(θ)=eθ/(1+eθ)，就得到logistic回归模型;μ(θ)=eθ，就得到研究计数数据的对数线性回归模型.

记μi(βn)=(μi1(βn)，···，μim(βn))T，Ai(β)=diag(σi1(βn)，···，σim(βn))，其中，diag(v)表示一个对角矩阵，其对角元素是向量v的元素.类似LIANG，ZEGER[2]，WANG[5]定义方程

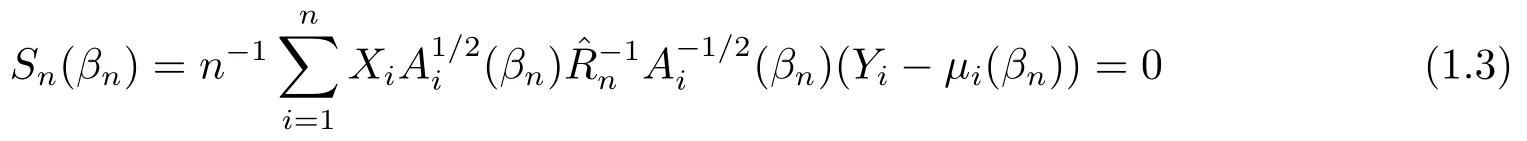
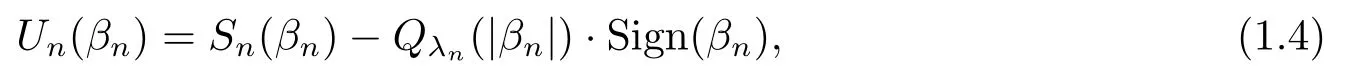
其中Qλn(|βn|)=(qλn(|βn1|)，···，qλn(|βnpn|))T，Sign(βn)=(sign(βn1)，···，sign(βnpn))T，Qλn(|βn|)·Sign(βn)定义为对应元素相乘得到的向量，SCAD惩罚函数为

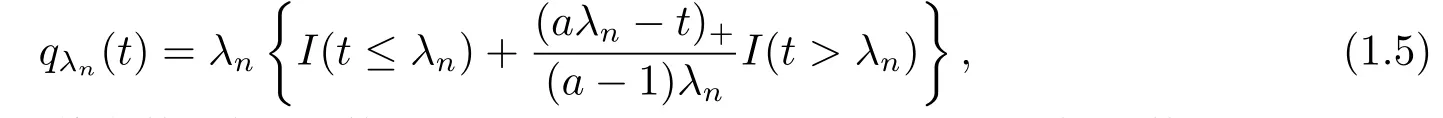
t≥0，a＞2，λn是调整参数，符号函数sign(t)=I(t＞0)-I(t＜0)，I是示性函数.

2.主要结果

在本文中，C，C1，C2，...代表与n无关的正常数，在不同地方可以表示不同值.为了得到我们的主要结果，需要如下假设条件.

(A1)pn维向量Xij，1≤i≤n，1≤j≤m的所有元素关于n一致有界;

(A3)存在与n无关的有限正常数C1和C2使得

其中Xij(1)是Xij的前sn个元素构成的向量，Xi(1)=(Xi1(1)，···，Xim(1))，λmin和λmax分别表示矩阵的最小和最大特征根;

(A4)Yi，i=1，···，n的共同真实相关阵Rn0满足Rn0≥CIm，估计工作相关阵满足其中是任意满足C1Im≤≤C2Im的正定阵，称为工作相关阵(可以不等于Rn0)，Im是m阶单位阵，‖R‖=[trace(RRT)]1/2表示矩阵R的Frobenius范数;

(A5)存在某个r＞2，对所有i≤n有E‖ϵi(βn0)‖r≤C，其中ϵi(βn)=(ϵi1(βn)，···，ϵim(βn))T

(A6)对所有1≤i≤n，1≤j≤m，βn∈Bn，方差满足μ的二阶导数¨μ和三阶导数μ(3)满足≤C，其中δ是任意正常数;

(A7)(i)min1≤j≤sn|βnj0|/λn→∞;(ii)(iii)λn→0;(iv).

定理2.1若假设条件(A1)-(A7)成立，则存在使下面式子成立，

其中Unk(βn)是Un(βn)的第k个元素，αn是任意固定的sn维单位向量，(2.3)和(2.4)经常被称为变量选择的Oracle性质.

注2.1条件(A1)更正了文[4]中笔误:pn维向量Xij一致有界.

注2.2(A3)减弱了文[4]中条件:的最小最大特征根都是n的阶.

注2.3(A5)减弱了文[4]中条件:存在正常数M2，M3使E[exp(M2|ϵij(βn0)|)]≤M3.因为ϵij(βn0)的矩母函数一致有界可以推出对任意r＞2有E|ϵi(βn0)|r≤C.

注2.4(A6)减弱了文[4]中条件:对所有1≤i≤n，1≤j≤m，其中特别当pn是n的高阶无穷大，文[4]中此条件较强.

注2.5(A7)减弱了文[4]中条件:在矩母函数一致有界条件下，文[4]中pn最高可达n2阶，我们的结果pn可达到nr阶，对任意r＞2.

注2.6将文[5]中条件和减弱为在参数真值点成立，即其中βn(1)∈Bn(1)={βn(1):

其余条件与文中[4-5]中条件一样.

3.主要结果的证明

引理3.1若假设(A6)，(A7)(ii)和成立，则其中βn∈Bn.

证由(A7)(ii)和知

由微分中值定理，(A6)和(3.1)，知

由(3.2)和(A6)，知

同理，由微分中值定理，(3.1)，(3.3)和(A6)，知

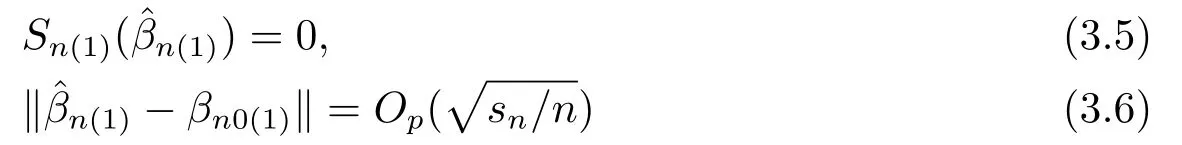
引理3.3[7](微分中值不等式)设D⊂Rn，f:D→Rm.若f(x)在D内可微，则对任何两点a，b∈D，必存在ξ=a+θ(b-a)，0＜θ＜1，使得

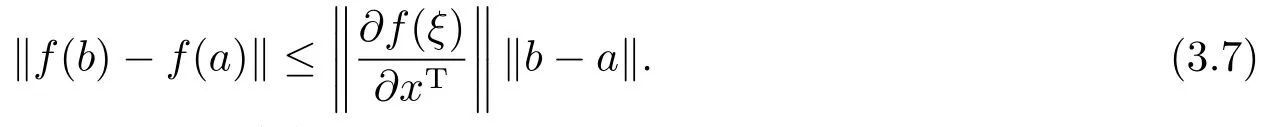
引理3.4[8]设X1，X2，···，Xn是鞅差序列，r≥2，则

引理3.5[4]记epnk表示第k个元素是1，其余元素都是0的pn维向量，

则

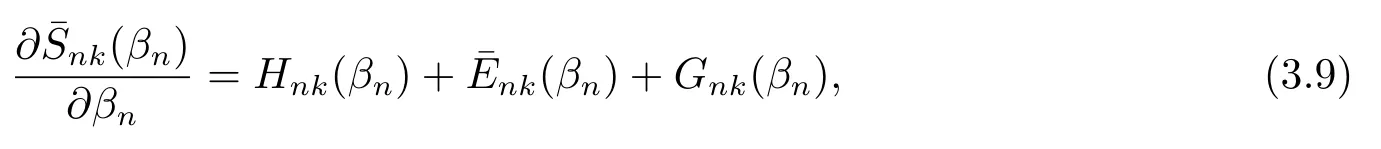
其中

注3.1文[4]中Gnk(βn)与文[5]中(βn)表达式的有笔误，应为

定理2.1的证明由假设条件和引理3.1知，引理3.2的条件满足，因而其结论成立.所以若取即

其中Snk()是Sn()的第k个元素.

由引理3.3，引理3.1，(A1)，(A7)(ii)，知

由(3.12)，(3.13)知

由假设条件(A1)知

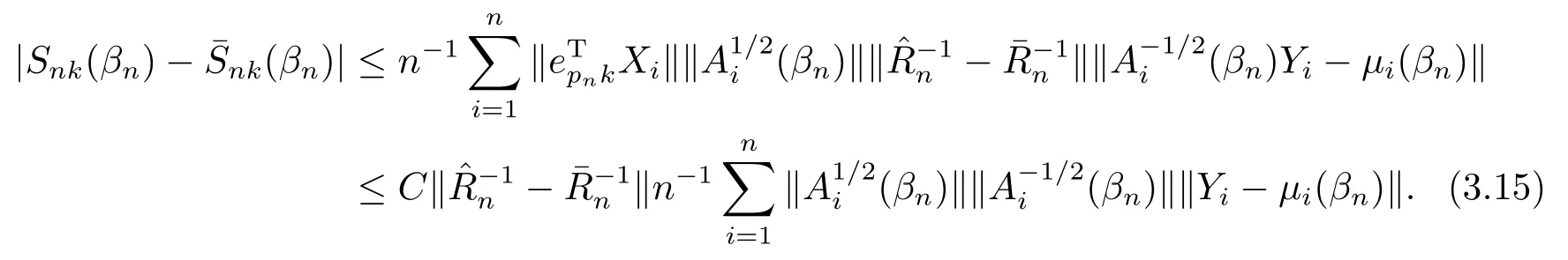
由(3.15)，(A4)，引理3.1，Markov不等式，(3.14)和(A7)(iv)，知

由泰勒公式，知

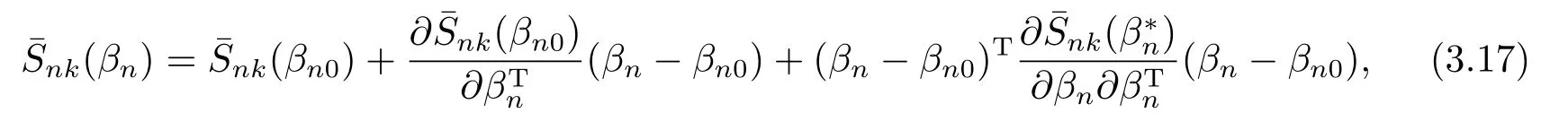
其中在βn与βn0的连线上.特别当有

其中Δnk(1)(βn)是向量的前sn个元素构成的向量，Dnk(1)(βn)是左上角的sn×sn矩阵.

由Markov不等式，引理3.4，(A1)，(A4)，(A5)，(A6)和(A7)(v)，知

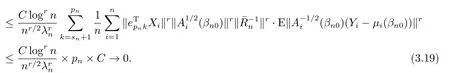
记Hnk(1)(βn)，nk(1)(βn)，Gnk(1)(βn)分别是向量Hnk(βn)，nk(βn)，Gnk(βn)的前sn个元素构成的向量，则由引理3.5知

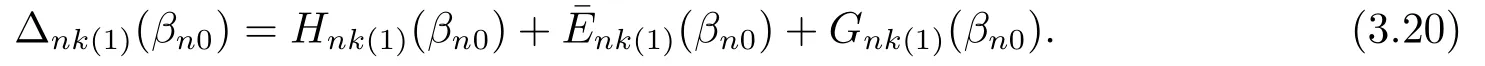
由(A1)，(A4)，(A6)和(A7)(iv)，知

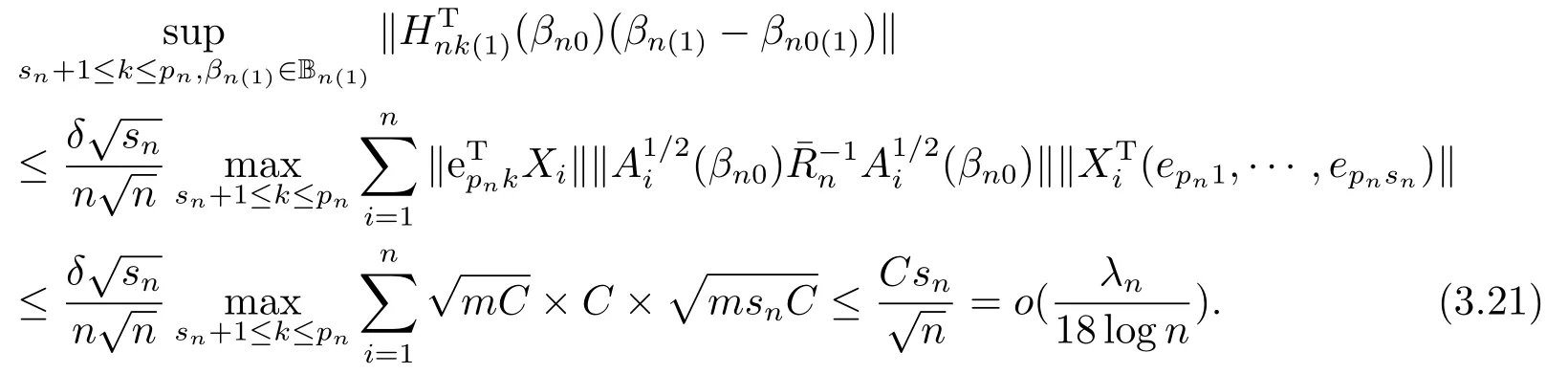
由引理3.4，(A1)，(A4)，(A5)和(A6)，可得

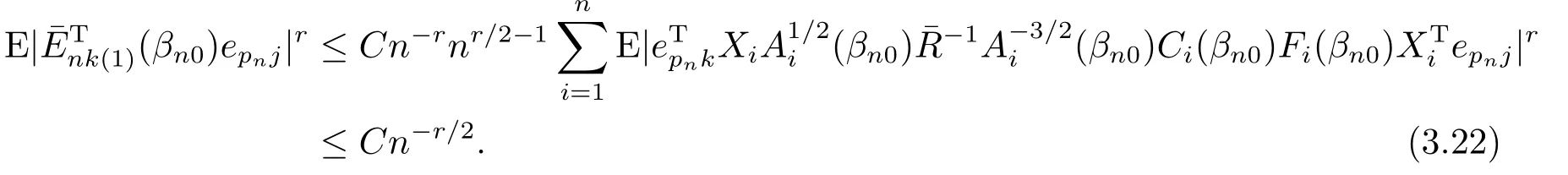
由Markov不等式，Minkowski不等式，(3.22)，(A7)(ii)和(A7)(v)，知

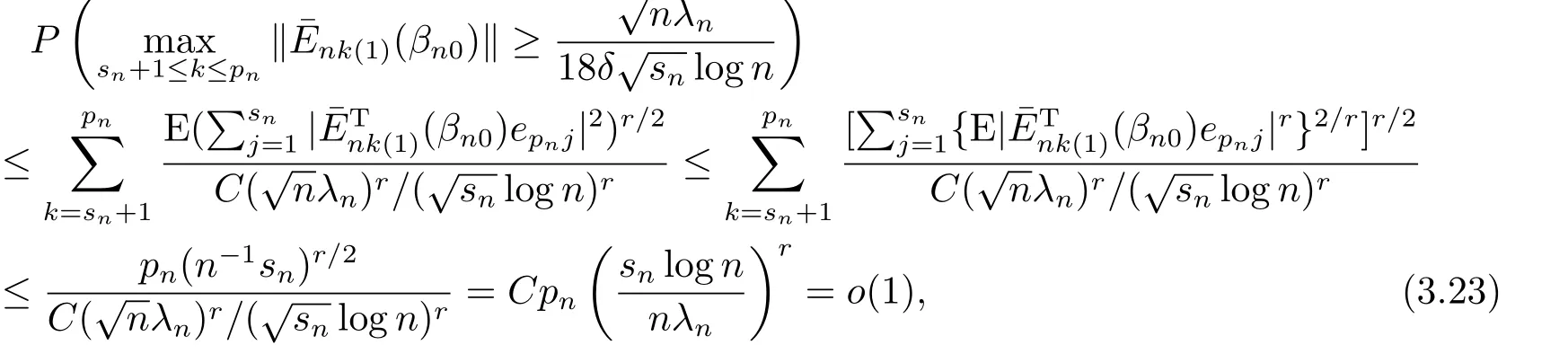
所以

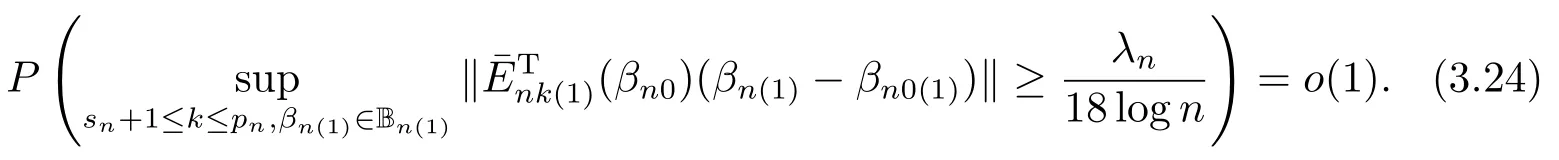
同理，

由(3.20)，(3.21)，(3.24)和(3.25)，得

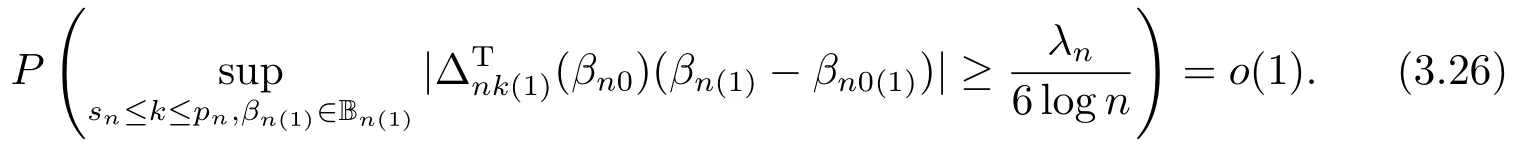
设emj表示第个j个元素是1，其余元素都为0的m维向量，则由可得，

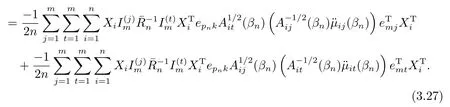
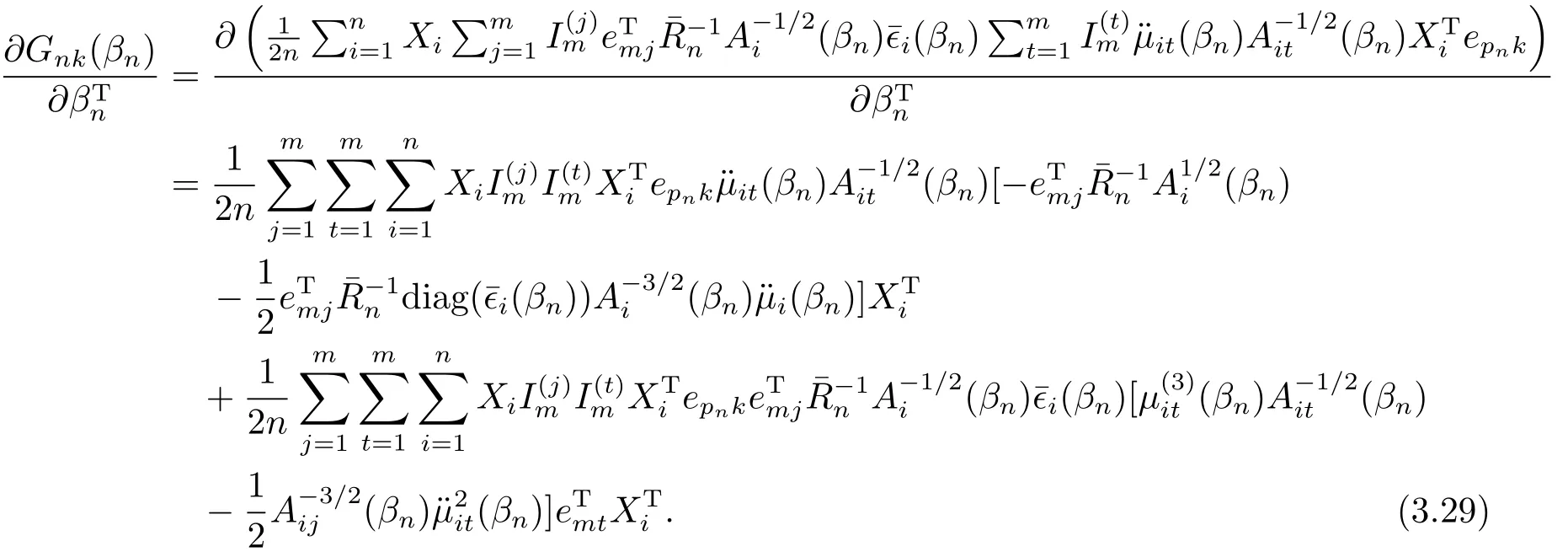
由(3.29)，(3.28)，(3.27)，引理3.5，(3.14)，(A1)，(A4)，(A6)和引理3.1，可证

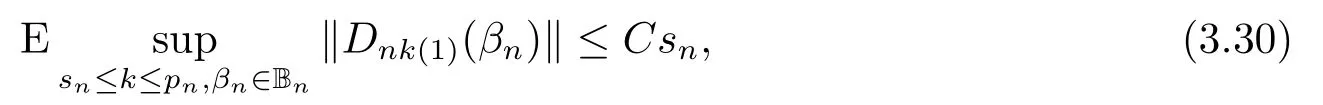
所以

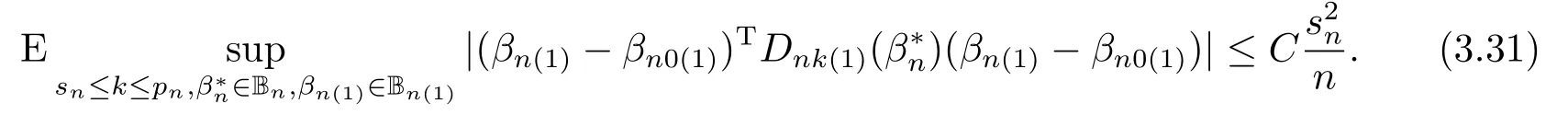
再由Markov不等式，(A7)(iii)和(A7)(iv)知

由(3.32)，(3.26)，(3.19)，(3.18)，(3.16)和(3.6)，知

当k=sn+1，···，pn，=0，所以再由(3.33)知(2.2)成立.由=知(2.3)成立.由假设条件，引理3.1和引理3.2知(2.4)成立.定理2.1证毕.

4.结语

本文只在较弱的条件下证明非零回归系数的个数发散情况下，纵向数据GEE的协变量选择的相合性质和Oracle性质.数值模拟请参看文[4].