考虑时变奖励的多摇臂算法在动态定价中的应用
乔勋双,毕文杰
中南大学 商学院,长沙410000
随着互联网技术的迅猛发展,大数据正以“侵略”式的速度蔓延并占领金融、保险、医疗、零售、物流、电子商务及电信等具有突出代表性的行业[1]。收益管理作为一种以数据分析为基础、以价格策略为核心的现代管理手段,随着大数据等相关技术与应用的发展,正在产生巨大变革。计算机技术的提高,互联网的普及和电子商务的蓬勃发展,大大降低了企业由于调整价格所带来的额外交易成本[2]。动态定价也因此被广泛应用于酒店、金融、互联网、零售业、电信、能源供应和旅游等行业。Jacobson等[3]指出企业定价提高1%,企业的运营效益往往能提高7%~15%。研究与实践也表明,动态定价确实能够显著提高企业的收益[4]。Gallego等[5]最早将动态定价和收益管理联系起来,采用强度控制理论研究了易逝品的动态定价问题。Carvalho等[6]考虑如何动态调整商品价格,使得有限时间段内的收益最大。
在此背景下,越来越多的学者采用算法定价的方法来确定其商品和服务的收费标准[7]。算法可以较好地通过观察消费者的购买过程,并根据其特征动态甚至个性化地制定价格[8],因此研究了多摇臂算法在动态定价问题上的应用。多摇臂是一个简单但非常强大的算法框架,可在需求等相关信息不确定的情况下随时间的推移做出决策[9-10]。其主要用于研究决策者面临探索-利用权衡的经典问题,而动态定价涉及在变化的市场环境中对产品或服务进行最优定价,通常会在最大化即时奖励和学习未知环境属性之间产生权衡[11],这种利用-探索权衡在动态定价领域得到广泛研究[12-13],因此多摇臂算法可以帮助决策者在学习过程中选择合适的摇臂以实现更好的利润。
置信区间上界算法最早由Lai等[14]提出,该算法借鉴类似于贝叶斯学习的思想,将估计的不确定性引入到解决方案中。随后由Rothschild[15]第一次在文章中将动态定价建模为多摇臂赌博机问题。Degroote等人[16]将在线算法的选择问题建模为多摇臂问题,基于Epsilon贪婪算法实现了在线算法自动选择的强化学习算法,并通过实验验证了该算法的有效性。Kleinberg等[17]提出了有限时间水平下动态定价问题的最差后悔公式,并被广泛使用。Chen等人[18]研究了不确定需求下的联合定价与库存问题,他们假设产品的需求分布函数来自一个参数未知的分布族,并在有限的价格变动次数约束下提出了相应的定价算法,并证明了其后悔值。Besbes等[19]研究了在给定初始库存情况下单产品的收益问题,目标是在一个固定的销售层级上动态调整价格以最大化期望收益。随后Besbes等人[20]提出了离散时间框架下无库存约束的动态定价算法,该算法假设产品的需求为线性函数,并根据该线性需求函数来对产品定价,结果表明尽管该需求函数可能是错误的,该算法的期望累计后悔值仍不高于O*(n-1/2)。Braverman等人[21]的研究中将摇臂视为独立的策略型代理人,研究了策略型多摇臂问题。而在一些多摇臂问题的经典研究中,是假设摇臂的奖励分布不随时间变化的,因此考虑时变奖励的多摇臂算法更加适用于动态定价场景中。Vakili等人[22]研究了奖励分布随时间任意变化的多摇臂问题。Garivier等[23]也表明经典的摇臂问题提出的学习策略可被应用于非静态场景中。
考虑到传统的多摇臂问题经常忽略摇臂的奖励分配随时间变化这一特征,因此研究了奖励分布是如何随过去摇臂的选择而变化的,首先对厂商的收益进行建模,其次将商品的定价问题描述为一个多摇臂问题,并构建利润最大化模型。最后,考虑到动态定价是一个非固定性的多摇臂问题,因此构建了利润随时间变化的定价模型,研究更加符合实际场景的动态定价问题,为厂商定价提供相应的决策支持。
1 模型构建
基于置信区间上界算法,研究了需求不确定下,考虑时变奖励的算法在动态定价问题上的应用。算法所考虑的场景如下,在一个多摇臂问题中,赌徒需要从多个摇臂中选择一个,每选择一个摇臂将获得相应的奖励,每个摇臂的奖励分布未知。只有当某一个摇臂被选择时,奖励分布情况才会被观察到,赌徒的目标就是在给定的时间水平下,最大化累计的期望奖励。将该场景对应在定价问题中,摇臂即对应于价格,厂商每次选取一个价格对商品进行定价,消费者将自身对该商品的保留价格与厂商提供的价格进行对比,若厂商提供的价格高于消费者的保留价格,则消费者不购买商品。反之,购买商品厂商获得奖励。这里需要注意的一点是,在定价问题中尤其是动态定价,每个摇臂的奖励分配是随时间变化的,这在传统的多摇臂问题中常被忽略。因此基于传统的多摇臂算法,研究了考虑时变奖励的多摇臂算法在动态定价领域中的应用。
1.1 相关参数及假设
相关使用符号说明与假设如下:
K:价格集合包含的价格个数。
i:价格序号,i∈{1,2,…,K}。
t:时间序列,t∈{1,2,…,T}。
T:时间水平。
p i:商品的价格。
c:商品的成本。
θt:t期到达的消费者商品的偏好,也为保留价格。
r i,t:第t期,价格为p i时所获得的利润。
p I*:最优摇臂,即使得利润最大化的价格。
I*:最优摇臂的索引下标。
μi,t:第t期价格为p i时所获得的期望奖励。
R(T):后悔值。
n i:价格p i被选择的次数。
α:控制探索的程度,即置信区间的宽度。
λi:价格为p i时商品的需求率,λi∈[0,1]。
在文章所描述的场景中,厂商是垄断的,并在与消费者交易的过程中实时制定商品的价格以最大化利润。具体假设为:
假设1假设存在一组包含K个价格的有限价格集合,厂商可从该集合中选择价格对商品进行定价。且当价格p1<p2<…<p K时,有商品需求率λ1>λ2>…>λK,且需求率在整个销售过程中不发生改变。
假设2假设每种商品都有大量的潜在消费者,每个消费者对商品有单位需求量。消费者的保留价格为θ,当且仅当且p≤θ时,消费者购买一单位商品。
1.2 商品定价模型
假设一个垄断厂商向多个顺序到达的消费者销售商品,厂商按照消费者到达顺序提供相应的商品报价,用p表示,且p≥0,消费者可以决定是否接受厂商的报价并购买商品。其中,商品的成本为常数c,由于文章假设厂商只销售一种商品,所以商品的成本c固定不变。每一个顺序到达的消费者对商品有不同的保留价格,由参数θ表示。此外,假设θ是在[0,1]上独立分布的。因此由每一时期到达一个新的消费者可知,当且仅当p≤θ时,消费者会购买一单位该商品,否则不购买。则每一时期,厂商可获得的利润为:

利润r(p)可被看做一个参数为θ的函数,若已知θ和价格p的分布,期望利润可表示为:
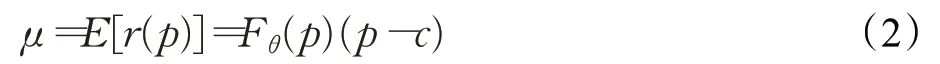
其中,Fθ(p)表示保留价格为θ的消费者接受价格p并购买商品的概率,基于多摇臂算法原理,厂商的目标是动态地调整价格并提供给消费者以最大化期望利润。然而,每一个消费者的θ对于厂商来说是未知的,这使得厂商很难做出最优决策,因此假设Fθ(p)的分布对厂商是已知的。
1.3 多摇臂框架
厂商在与依次到达的消费者进行交互时,通常采用探索-利用均衡来最大化即时利润,即利用当前信息选择迄今为止能够带来最高利润的价格对商品进行定价,或者选择探索在未来时间回合中可能带来更高利润的价格。
在动态定价问题的研究中,对于上述探索-利用均衡问题,通常会设计一个学习策略来动态地调整价格,使厂商利润最大化,该过程被形式化为一个随机多摇臂问题。因此首先介绍多摇臂问题的一些基础知识,然后讨论如何构建一个价格随时间变化的动态定价模型并研究其对利润的影响。
首先将定价问题描述为一个动态优化问题,考虑一个以时间为序列消费者顺序到达的场景,在每一回合t∈{1,2,…,T},消费者的保留价格为θt。根据多摇臂算法,将p i∈P定义为一个摇臂,若消费者的保留价格θt≥p i,则消费者购买该商品,对于每一个摇臂pi∈P,在t∈{1,2,…,T}时获得的期望奖励为:

考虑在事先未知Fθ(⋅)的情况下,厂商采用学习策略来获取最优摇臂,在t时被选择摇臂的下标索引可表示为I t。学习策略的效用可用后悔值regret[24]来评估,由学习策略累计的期望奖励与最优摇臂所累计的奖励之差计算而来。由于这两种奖励和摇臂的选择都是随机的,因此后悔值通常可表示为:

1.4 学习策略
作为统计学的标准工具,置信区间通常用于处理多摇臂中的探索-利用均衡问题。对基础的置信区间上界算法进行改进,构建利润随时间变化的动态定价模型,来处理上文所描述的非固定性的多摇臂问题,以更加精确地估计期望奖励。
1.4.1 置信区间上界算法
置信区间上界算法由Bouneffouf[25]提出,其基本思想是通过将所观察到摇臂的历史奖励进行线性组合来估计每个摇臂的未知期望值。在学习过程中,变量n i=表示截止t期p i被选择的次数,变量表示样本平均奖励,也被看作真实期望奖励的估计,则真实期望奖励r i的置信上界为。其中lnt表示t时期的自然对数(e≈2.718 28的该数次幂等于t),式中的根号项是对摇臂p i估计值的不确定度或方差,α>0控制了探索的程度,即置信区间的宽度。每当摇臂pi被选择时,ni增加,因为其出现在分母中,所以不确定性减小了。在另一方面,每当除摇臂pi之外的摇臂被选择,t增加而n i保持不变,则不确定性增大。
自然对数的使用意味着增长的速率逐渐变慢,但其值依然会趋近于无穷大。在每一期,都选择置信区间上界最大的那个摇臂作为最优摇臂,最优摇臂表示为:

如果忽略摇臂期望奖励的时变性,可以直接将置信区间上界算法应用于定价问题。该策略的详细描述如算法1所示。
算法1 UCB
输入:α∈R+

1.4.2 考虑时变奖励的置信上界区间算法
算法1描述了一个基础的随机多摇臂算法,每个摇臂都与奖励的时不变分布相关联,其中最优摇臂不随时间变化。然而动态定价是一个非固定性的多摇臂问题,即真实的奖励会随时间变化。因此接下来对算法1进行改进,构建利润随时间变化的模型,来处理非固定性的多摇臂问题,以更加精确地估计期望奖励。
对于任意价格p i∈P,厂商都面临着未知的真实需求,对应式(3)中累计分布Fθ(⋅),代表了每个价格p i被消费者接受并产生购买行为的概率,可用表示,其中ni,t表示截止时间t时,价格p i被消费者选择的次数。厂商得到相应的利润为r i=pi-c,则对于每一个摇臂p i∈P,在t∈{1,2,…,T}时获得的期望奖励为:

通过上式可看出每个摇臂的期望奖励是随时间变化的,其变化是视摇臂具体而定的,即最优摇臂并不是固定不变的。基于公式(6),对算法1进行修改,通过构建算法2来描述摇臂的奖励如何随时间变化的。将该学习策略称为VarUCB,算法的详细步骤见算法2。
算法2 VarUCB
输入:α∈R+

2 仿真分析
提出了考虑时变奖励的置信区间上界算法,为了评估其效用,使用真实数据进行仿真分析。接下来的章节,首先介绍了所使用的数据集,并对数据集进行预处理接着对数据进行预处理,对上文提出的两种学习策略进行对比分析。最后基于仿真分析的结果,对比上述两种学习策略的效用,寻得使厂商利润最大的价格,为厂商的定价决策提供相关参考。
2.1 数据集描述
数据来自日本最大的团购网站Ponpare,文章使用的原始数据集包含消费者和各种类型商品的相关数据,包括美食、健康医疗等,一共七个数据集分别为Coupon_list、user_list、Coupon_detial、Coupon_visit、Coupon_area、Prefecture_location、Sample_submission,主要字段为价格、购买时间、性别、年龄等。
通过各数据集的主键如USER_ID_hash、COUPON_ID_hash等将各个数据集进行关联,确定最终有效字段,第一列对应于算法的价格,第二列对应于奖励。整合后的数据集包含3 000多条数据,除去缺失值,使用870条数据对上文两种学习策略的效用进行对比分析。
2.2 学习策略的参数设置
假设每个消费者的保留价格θt服从μθ=0,σ=1的正态分布N(μθ,σ2),考虑θt可能会超出[0,1],因此定义θt为:

K:在所有的仿真过程中,K都设为10。
α:在算法1、算法2中,输入参数α控制了所估计的期望奖励的置信区间的宽度。
T:设置时间水平T=1 000。
2.3 评估方法
在本文前面的章节中提出了UCB和VarUCB这两种学习策略,并对这两者的模型效果进行了对比分析,现令pt表示厂商在t时期提供给消费者的报价。厂商的目标是设置最合理的价格令消费者接受并购买商品以获得最大收益,因此使用实际的收益值去衡量学习策略的效用。假设t时期后不再有消费者光顾,则厂商的总收益为:

2.4 仿真结果分析
2.4.1 参数分析
仿真分析的第一步即要明确所描述的两种算法在参数α不同的情况下其平均奖励值是如何变化的,以及确定每一种算法的最优参数值。因此为了展示上述两种学习算法在每一参数α下随时间变化的学习过程,使用前1 000步奖励的平均值来表示每一种算法完整的学习曲线,这一值与学习曲线下的面积成正比。
结果如图1所示,各个算法的学习曲线呈倒U形:即这两种算法在使用居中的参数值时表现最好。结果表明UCB算法和VarUCB算法的最优参数值α近似等于21,且在α=21的情况下各自所学得的平均奖励值最大。此外图1展示的学习曲线还表示,在不同的参数下VarUCB算法的平均奖励值都高于UCB算法,且在到达最优参数值21之前,VarUCB算法学习曲线的增长幅度更快,表明VarUCB算法相较于UCB算法其收敛速度更快,进一步表明所提出的考虑时变奖励的VarUCB算法表现更佳。
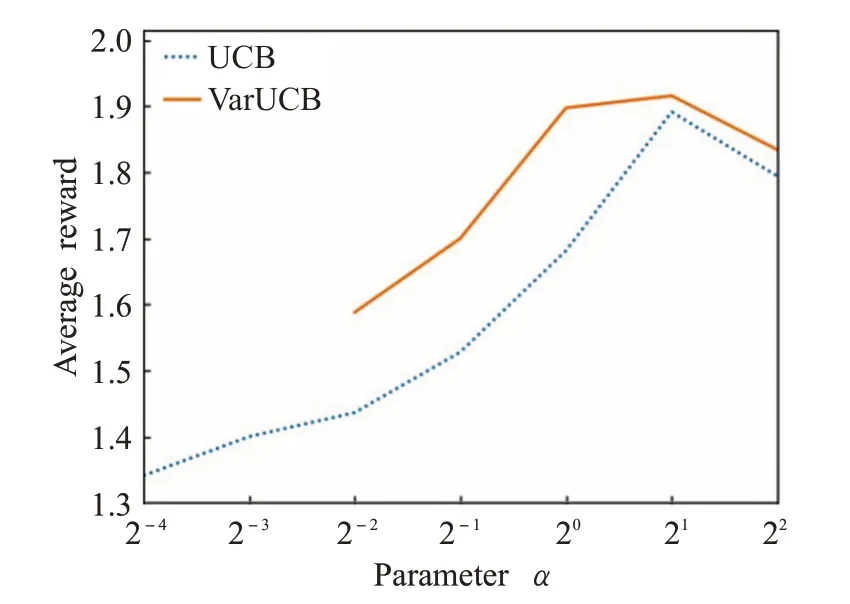
图1 参数审视图
2.4.2 奖励分布
在2.4.1小节中已经学得上述两种算法的最优参数α都为2,因此本小节在分析算法的奖励分布时将只分析α=2时各自的奖励是如何变化的。在参数α=2,T=1 000时,UCB算法和VarUCB算法下厂商获得的平均收益分布状况如图2所示。
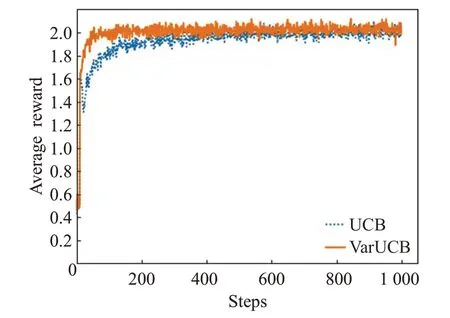
图2 α=2时奖励分布图
由图2可以看出,在消费者保留价格呈正态分布,α=2时,UCB和VarUCB算法有着相似的性质,即随着循环次数的增加,奖励分布逐渐趋于平缓,并逐渐接近真实奖励。但是在整个循环过程中可以发现,VarUCB算法的收敛速度相比之下快于UCB算法,且VarUCB算法所学得的平均奖励是略高于UCB算法更加接近真实奖励的。通过对比分析两种学习策略的平均奖励,结果表明VarUCB算法收敛速度更快,所学得的奖励更加接近真实奖励,能够使得厂商在交易过程中获得更高的收益。
2.4.3 后悔值分析
为了进一步对比上述两种学习策略的效用,通过使用算法计算了两种学习策略的后悔值regret,从另一个角度评估UCB和VarUCB算法的性能。具体步骤为,首先需要通过公式确定最优摇臂,接着对于每个价格pi∈P,在每一时期都设置价格p t=p i,计算出奖励U(t),通过比较两种学习策略的U(t)可以确定最优摇臂。最后通过公式R(t)=U*(t)-U(t)计算出每一时期的后悔值,U*(t)由最优摇臂确定。图3为在时间水平T=1 000,α=2时,两种学习策略的后悔值变化情况。
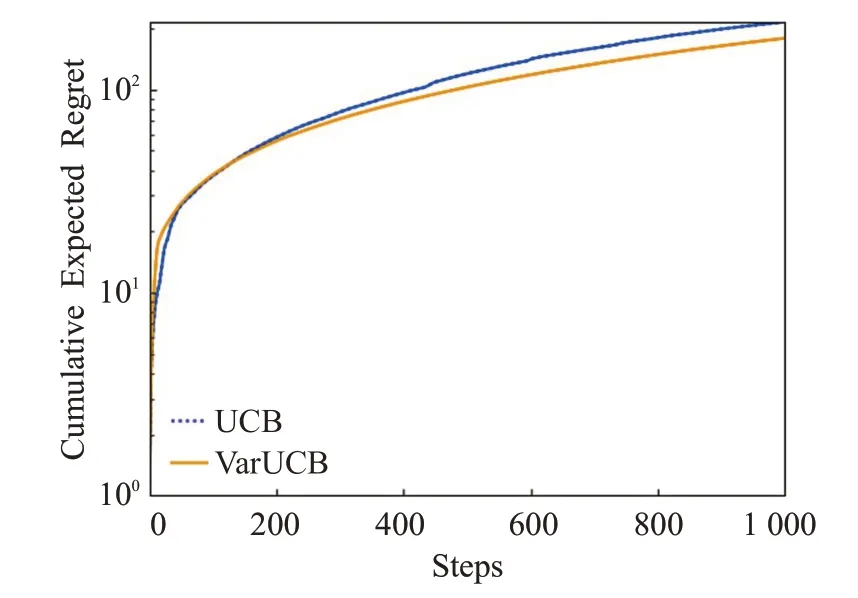
图3 后悔值分布图
通过对真实数据集进行仿真实验,结果表明,当α=2时,每一回合算法所选择出的最优摇臂都为p I*=0.8。对于后悔值分析,所取得的结果越小表明算法的效用更好。如图3所示,VarUCB算法的后悔值曲线收敛比UCB算法更快,且每一时期后悔值都低于UCB算法的后悔值,这表明所提出的VarUCB算法的效用更好。后悔值的评估结果表明,VarUCB算法学得的最优价格更加接近于真实的最优摇臂。
若算法所学得的价格低于最优价格,则厂商可选择一个较低的价格提供给消费者以促使他们进行购买。为了防止消费者感受到不公平对待,厂商可以向所有的消费者提供一个固定的价格。对于后悔值的评估结果,图3可以很好地表明通过采用提出的VarUCB算法,厂商能够以更高的概率学得最优价格,使得利润最大。同时发现学习策略所选取的最优价格对应于带来最大累计奖励的价格,这再次表明所提出学习策略的有效性。
3 结论
研究了在需求不确定情况下的产品动态定价问题,基于基础的多摇臂算法将商品的定价问题建模为多摇臂模型,提出了考虑时变奖励的置信区间上界算法,研究了其在动态定价问题上的应用。通过对真实数据进行仿真,将考虑时变奖励的置信区间上界算法与基础的算法进行对比分析,结果表明通过提出的算法所学得的奖励更加接近真实奖励,收敛速度更快,能够以较高的概率学得最优价格。因此通过仿真分析,在现实场景中,采用VarUCB算法定价可以帮助厂商以更高的可能性获得最高的利润,作出最优的决策。
目前,主要研究了厂商向消费者提供单一产品的场景,该场景容易实施但是多产品定价更加符合现实场景。因此在未来的研究中,会着重分析多产品定价问题,以考虑更加符合实际的场景。另外,考虑到消费者的保留价格可能会影响到厂商的定价策略,即消费者存在策略性行为,因此未来也会研究如何修改多摇臂模型框架和学习策略来应对策略型消费者。

