基于语义的UML类图的集成分类

袁中臣，马宗民

1.东北大学 软件学院，沈阳110819

2.沈阳工业大学 化工过程自动化学院，辽宁 辽阳111004

软件重用能节省开发费用和时间。随着软件复杂性的增加，软件重用开始出现在软件生命周期的每个阶段[1-2]。软件设计发生在软件生命周期的早期，对接下来的开发工作产生重要的影响。所以，软件设计的重用受到关注[3]。UML（Unified Modeling Language）类图由类和类之间的关系构成，用于系统的静态建模。UML类图被广泛应用于软件设计，已成为软件设计事实上的标准[4]。所以UML类图重用成为软件设计重用研究的重点[5-6]。随着可重用的UML类图数量的增加，分类成为一项基础性工作。

服务于软件重用的组件的分类在一些文献中被提出[7-10]。这里的组件是指程序代码、设计模型和规范等。所有提出的方法能被归于同一类，即，通过预先定义的属性（如开发平台和功能等）去描述每个组件，组件被表示为一个属性向量，向量差异（欧式或者余弦距离）用来度量组件相似性，然后应用分类算法实现组件的分类。

人为属性的定义不能完全表达一个UML类图的语义，并且属性的定义需要领域知识的支持。相似性度量是进行分类的重要一步，现有关于相似性度量的研究主要集中在语义[11-16]。文献[11]结合领域本体和应用本体计算类图之间的语义相似性，以增加准确性。文献[11]和[16]在匹配中考虑了关系的特征。文献[13]提出类图的相似性分为浅层（命名）相似性和深层（语义）相似性，并使用邻居类的信息实现关系的相似性度量。在文献[14]中，除去类之外，还将属性和操作列入语义度量范畴。所有以上这些方法都考虑到概念名称，并应用了本体的概念语义相似性。在语义相似性度量中，除了概念语义之外，还包括属性（操作）类型和访问权限等限制。即使是相同类的相同属性在不同项目中也可能被定义成不同的类型。如类“Student”的学号属性“num”在不同项目中可能被定义为“integer”和“String”两个不同的类型。而这些差别在接下来的编码阶段会体现出更多的差异。所以，本文定义的语义相似性度量将把这些因素考虑在内。

在UML类图中，把每个关系称为一个语义单元，即R=[端点类1，关系类型，端点类2]，语义单元之间的相似性计算从端点类和关系类型进行。类图之间的语义相似性即为所有语义单元的相似性均值。同时，在进行类的相似性度量时，除了考虑概念语义名称，把属性、操作及其类型和访问限制等也考虑在内。类图之间的语义相似性被定义如下：

分类在很多领域得到应用，如模式识别和机器学习等[17]。很多分类算法被提出，如决策树（DT）、遗传算法（GA）、逻辑回归（LR）、支持向量机（SVM）、K临近（KNN）和朴素贝叶斯（NB）等。除了这些单个的分类算法还出现了集成分类算法[18]，如随机森林等。由于集成分类能够克服单个分类算法的缺点，本文构建了一个基于KNN的二级分类的集成分类器E-KNN。这里实现的是单标签分类，即，一个UML类图仅能被分类到唯一的类别目录。

本文正是从语义方面提出对UML类图的分类。定义了类图之间的语义相似性度量，提出算法获取中心类图，基于中心类图和改进的KNN算法分别构建E1-KNN和E2-KNN分类器，并组成二级集成分类器E-KNN。实验验证了所构建分类器的有效性。

1 语义相似性度量

现有的基于本体的概念语义相似性计算分为两种方法：语义距离和包含内容[19]。本文选择被广泛使用的基于路径的语义距离来计算概念之间的语义相似性，表示如下：

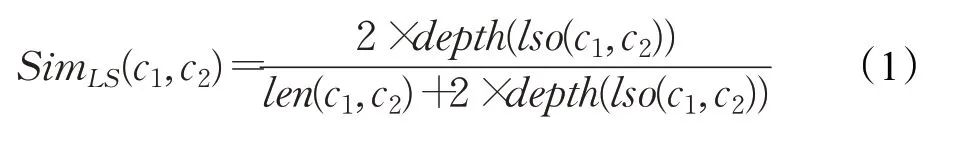
c1和c2分别表示两个概念，lso(c1,c2)表示概念c1和c2在本体（如WordNet）层级结构中的最低公共祖先；len(c1,c2)表示概念c1和c2的最短路径；depth(c)标识概念c在本体层级结构中的深度。

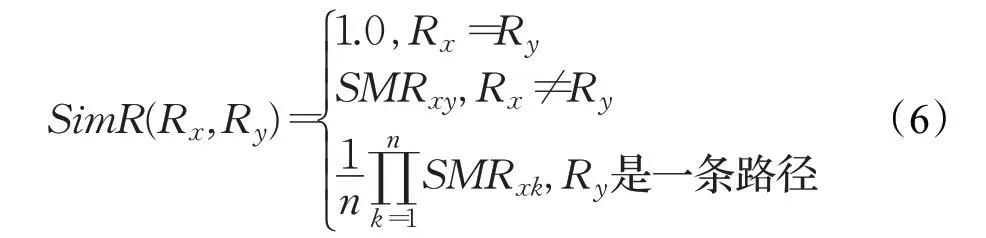
cd1和cd2是两个类图，|cd i|表示类图cd i中包含的关系的数目。类Ci来自类图cd1,A i和O i分别是类Ci的属性集合和操作集合，|A i|和|O i|分别表示包含属性和操作的数目。同理，类C j来自类图cd2,A j和O j分别是类C j的属性集合和操作集合。SimC、SimR、SimA和SimO分别表示类相似性、关系相似性、属性相似性和操作相似性。λ、α、β(β1,β2,β3)、γ(γ1,γ2,γ3,γ4)是权重因子。Root(c)标识一个概念名称c的词根，因为在属性和操作的表达中经常包含很多缩写，如属性“ID”实际上表示的是“i dentity”。SimT标识类型（返回值类型）相似性；SimP标识访问权限相似性。操作有时还包含参数，并且参数的定义和属性是一致的，所以参数的相似性度量(SimQ)采取和属性相同的度量方法。

考虑到建模相同项目可能会出现异构的类图，关系相似性度量SimR被总结为三种情况。当被匹配的两个关系类型相同时，相似性值为SimR=1.0；当匹配的两个关系类型不同时，引入文献[13]的关系相似性矩阵SM R获取相似性值。对于第三种情况，当一个关系被匹配到UML类图中的一条路径而不是一个关系时，定义公式来标识相似性。R i标识路径上每个关系的类型，n表示关系路径的长度。

为了度量属性（操作）访问权限和类型的相似性值，通过邀请软件工程领域专家以访问权限的限定范围差异和类型之间的转换复杂度为基准分别给出相似性值的评分，如表1和表2所示。

表1 访问权限相似性

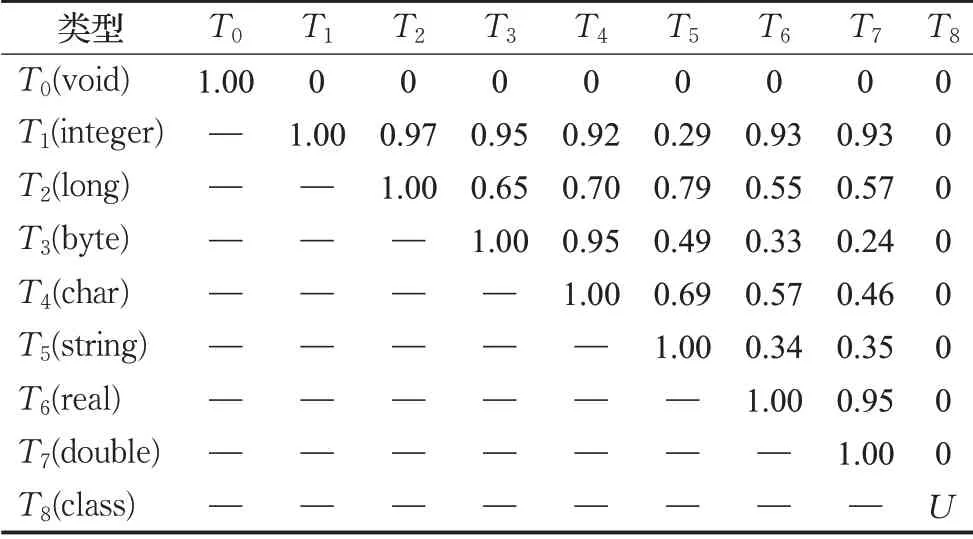
表2 类型相似性

在表2中，U表示两个类的相似性。如果匹配的两个类是相同或者存在继承关系，则U=1，否则U=0。这种相似性度量经常会出现在一些“依赖”关系的类图匹配中。

2 集成分类

2.1 中心类图

每个类别的类图都表现出相似或者相同的特征，找出这些特征是分类的首要一步。这里定义中心类图标识每个类别目录中类图的特征。

定义1中心类图在目录C i中，如果类图cd j和所有其他类图之间的平均相似性值高于其他类图，则cd j被称为中心类图。

取一组中心类图来表示一个目录的特征。接下来的问题变成了如何去获取中心类图集合，这里提出一个行最大值捕捉的算法。假定一个目录Ci中包含的类图的数量是n，那么就会存在一个n×n阶相似性矩阵SM,SMij表示类图cd i和cd j之间的相似性值。行最大值捕捉算法被描述为算法1，描述如下：

算法1获取目录中心类图集合

输入：相似性矩阵SM和中心类图数目center Num

输出：中心类图集合center CDs

其中，中心类图集合centerCDs初始化为空。计算SM每一行的平均值(row SimAVG)，从中找到最大值，该行对应的类图即为一个中心类图cd p，如果中心类图集centerCDs中不存在cd p（有时候目录中会出现两个完全相同的类图），则插入，然后从SM中删除这个类图对应的行和列，继续在SM中查找下一个中心类图，直到找到指定数目center Num为止。

假定一个目录的类图数量为n1，则获取目录中类图的相似性矩阵的时间复杂度为；要寻找中心类图数量为m1，则在目录中查找特征类图的复杂度是O(m1×n1)。所以，总的时间复杂度为

2.2 分类流程

本文构建了一个2级分类的集成分类器E-KNN，如图1所示。

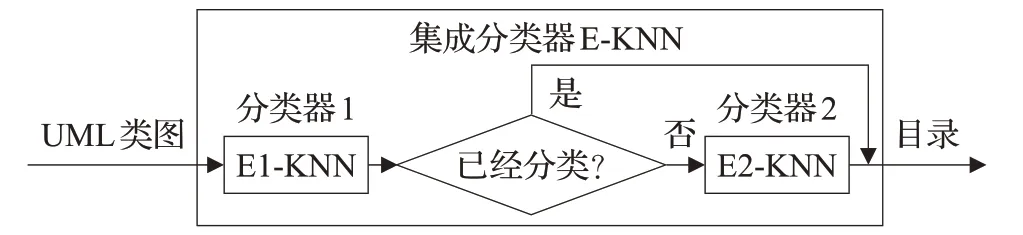
图1 集成分类器E-KNN

分类过程分为两个阶段。UML类图首先进入分类器E1-KNN进行初级分类，产生可能分类的目录。然后，由分类器E2-KNN决定最终分类目录。很多情况下，分类结果也能由E1-KNN直接决定，而不需要进入E2-KNN。E1-KNN和E2-KNN都是基于KNN算法。在KNN中，所有样例参与相似性计算，所以存在分类效率低问题[20]。同时，K的设置和样例分布也影响分类的准确性。这些问题需要在E-KNN中考虑。

2.2.1 E1-KNN分类器

E1-KNN的分类计算是基于中心类图集合，而不是所有训练样例，相似性计算次数明显减少。E1-KNN分类器的分类可能产生3种结果：

（1）类图不能被分类到现有的目录。

（2）类图被分类到一个确定的目录。

（3）输出初级分类目录。

针对结果（1），标记不属于现有分类目录为C0。当在最高的的K个相似性中，属于分类目录的平均相似性值μ＜μ0时，类图不能被分类到现有目录，即分类到C0，分类过程终止。

针对结果（2），这里规定，当在最高的K个相似性值中属于分类目录的类图的数量w≥w0，分类目录确定，分类结束。

表3 训练样例的特征

参数μ0和w0能通过训练获得，训练过程如下：

步骤1获取目录中心类图集合，将所有训练样例分为中心类图(m)和测试类图(n-m)两个集合。

步骤2计算每个测试类图和每个中心类图的相似性，并基于KNN进行分类。

步骤3计算每个测试类图的μ和w。

步骤4统计所有测试类图正确分类的比率λ1，如果λ1＜λ0(λ0为预先设定，一般λ0≥0.90)，重新设定每个目录中心类图的数量（如m0=m0+1），并返回步骤1。否则，获得

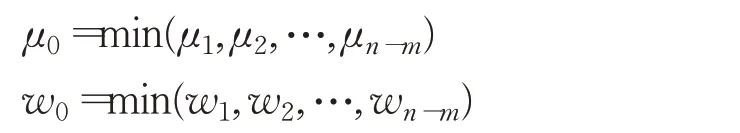
训练参数的时间复杂度为O(r×m×(n-m)),r为迭代次数，一般在3～7次可以完成参数训练。

针对结果（3），取最高的平均相似性值对应的目录（通常不会超过3个）作为分类器E1-KNN的输出。

E1-KNN的具体分类流程如图2所示。

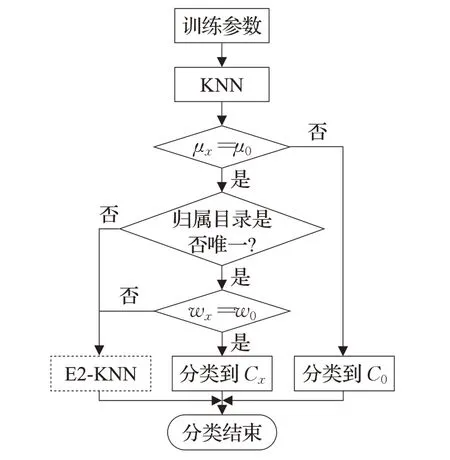
图2 E1-KNN分类流程

在E1-KNN中，类图被分类到现有目录的必要条件是分类目录唯一，充分条件是μx≥μ0和w x≥w0。同时，C0的标识可以为将来扩展未知类别类图的分类提供支持。

2.2.2 E2-KNN分类器

E2-KNN分类计算是基于E1-KNN输出目录的样例而不是所有样例，所以效率明显提高。同时，在处理K（高于E1-KNN中的K值）个最高相似性值中属于不同目录的类图数量相等的问题时，针对训练数据分布情况分别给出解决方案。

（1）K+X。即，扩大K的范围，然后获取分类目录。通常，X=K/2。这种解决方案的前提是不同目录的样例分布均匀。

（2）目录平均值。分别统计属于不同目录的样例对应的相似性平均值μ，类图被分类到平均值高的对应的目录，此方案适用于样例分布不均匀的情况。

E2-KNN主要针对建模交叉领域项目的类图的分类。这些项目的类图包含来自不同领域的语义信息，经常不能通过基于有限的中心类图的分类器E1-KNN给出确定的分类目录。

3 实验结果分析

3.1 实验数据

实验中使用的UML类图来自Google（Searchcode）的Java代码的反向工程[21]。训练样例分为五个领域，分别为教育(C1)、医疗(C2)、金融(C3)、房地产(C4)和电子商务(C5)等。为了验证样例分布和尺寸均匀与否对分类的影响，样例被分成4个组，每组500个，细节如表3所示。此外，200个类图被用于测试，其中，20个测试样例来自非上述领域(C0)。同时，包含交叉领域信息的类图的数目也是20。使用Java语言实现了本文所提出的分类方法，并且在PC机（Win 10，Intel Core i7，RAM 8 GB）上执行。语义相似性计算权重参数设置：λ=0.3,α=0.5,β=0.3,γ=0.2,β1=0.5,β2=0.3,β3=0.2,γ1=0.4,γ2=0.3,γ3=0.2,γ4=0.1。通过训练获得分类器E1-KNN中参数设置，如表4所示。

表4 参数设定

3.2 结果分析

分类质量可以从准确率P、完成率R和二者调和平均值F三个指标来度量。这里设定A表示正确地分类的测试样例的数量；B表示错误地分类的测试样例的数量；C表示应该分类但是没有分类的测试样例数量。P、R和F公式为：

测试样例在4个训练样例组上执行分类获得的分类质量如图3所示。

图3 E-KNN分类质量

可以看出，g1获得分类质量最高，g4最低，总体差别不大。无论哪个样例组，分类的完成率要高于准确率。这是因为，经过两级分类不能最终决定分类目录的样例数量很少。

从分布上看，分类质量受样例分布的影响不大。如由g1和g3获得的分类质量差异很小，同样的事情也发生在g2和g4上。这是因为，在E1-KNN中使用了中心类图，而中心类图在分布均匀和不均匀的样例中的数量差异不大，这也屏蔽了分布差异对分类的影响；在E2-KNN中，提出的平均相似性的计算也避免了分类受分布影响的问题。

样例尺寸差异还是使得分类质量表现出不同，尽管不大。由均匀尺寸的训练样例获得的分类质量要高于不均匀尺寸获得的分类质量，如g1和g3分别高于g2和g4。这是因为，大尺寸的类图就包含了更多的语义信息，而小尺寸的类图包含的信息较少。当一个小尺寸的类图进行分类时偶尔会被分类到错误的大尺寸类图的目录，特别是对于交叉领域的测试样例。如测试样例中关于“医疗学校”的UML类图，有时会被错误地分类到“医疗”领域，尽管它应该被分类到“教育”领域。

接下来，将上述集成分类（E-KNN）获得的分类质量（F值）和分别由一级（E1-KNN）和二级（E2-KNN）分类获得的分类质量进行对比，结果如图4所示。

可以看出，由E-KNN获得的分类质量明显高于仅由分类器E1-KNN和E2-KNN获得的分类质量。E1-KNN在分类交叉领域类图时有时不能决定最终目录，而E2-KNN不能处理C0的问题，且受训练样例分布影响较大。由E1-KNN和E2-KNN结合组成的E-KNN恰好有效地解决了这些问题。

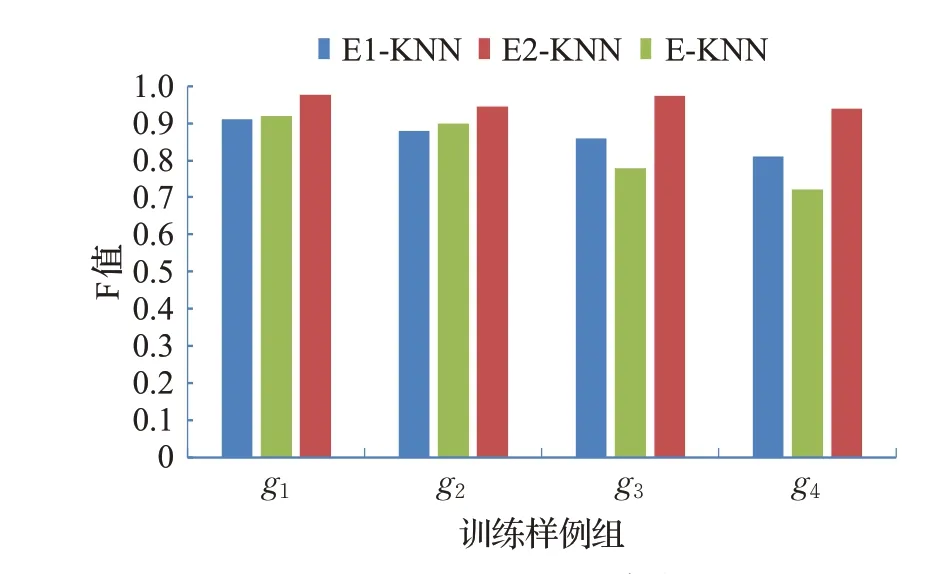
图4 一级和二级分类质量对比

最后，将获得的分类质量（F值）和（平均）效率与由常用分类算法KNN、NB、LR、SVM、EN（KNN（4）和NB（3））获得的结果比较。因为LR和SVM被用于二分类，这里训练样例为5个类别目录，所以，分别训练了5个分类器（一对多）实现多分类，以函数值决定分类目录。分类器EN是分别由基分类器KNN和NB构成的集成分类器，分类结果通过举手表决。中心类图中的类组成NB、LR和SVM的特征。所有分类方法均使用提出的相似性度量。分类质量和效率比较如图5和图6所示。

图5 分类质量比较

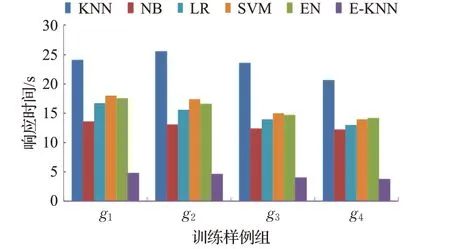
图6 分类效率比较

从分类质量上看，几种分类器在样例组g1获得的分类质量最高，而由样例组g4获得的分类质量最低。提出的分类方法获得的分类质量要优于其他分类器。同时，也能看到，单分类器的分类质量受到分布的影响。集成分类器EN的分类质量要优于单分类器。在单分类器中，KNN分类质量最高。从分类效率上看，提出分类器的分类效率要优于其他几种分类器，尤其是KNN分类效率最低，每次分类都需要大量的相似性计算。中心类图的引入减少了大量的计算。同时，两级分类使得很多测试样例的分类直接由分类器E1-KNN给出结果，而没有进入分类器E2-KNN。所以，无论从分类质量还是从分类效率上比较，本文提出的分类方法都要优于其他分类器。

4 结束语

本文以UML类图的重用为背景，从语义上提出UML类图的分类。定义了类图的语义相似性，提出算法获取中心类图标识目录特征，基于改进的KNN分别构建了E1-KNN和E2-KNN，并组建了集成分类器E-KNN。实验结果表明，本文提出的两级集成分类器解决了其他分类器受计算量影响而产生的效率问题，也解决了受分布和尺寸影响而产生的分类质量问题，和其他几种分类器相比具有显著优势。在接下来的工作中，尝试结合其他算法提高效率是一个主要方向。此外，将语义分类和结构分类相结合以实现类图的混合分类是另一个将要开展的工作。