Map Reduce技术在物资调运与配载问题中的应用
陈元文
武警工程大学 装备管理与保障学院,西安710086
MapReduce是由谷歌公司开发并已广泛使用的一种并行计算编程框架,采用“分而治之”的思想,通过将一个复杂的串行任务分解为多个独立的并行任务而提高计算效率[1],是云计算的重要技术基石之一。MapReduce技术所具备的高度自动化和强大的容错能力,使智能算法摆脱了以网格计算为代表的传统并行化方案对运行环境的繁琐设置过程,摆脱了其对高性能和高稳定性硬件设备的依赖。
基于以MapReduce为代表的云计算技术的智能算法,因其高性价比和高容错性,从2008年逐渐引起学术界的广泛关注。Xu和You[2]为分析多层陶瓷基复合材料在冷却过程中的热残余应力对材料寿命和材料性能的影响程度,设计了基于多次迭代的改进MapReduce的粒子群算法,并结合有限元分析法对优化模型进行了求解。吴昊等[3]使用云计算技术将蚁群算法并行化,提出融入分治思想和模拟退火算法的基于MapReduce的蚁群算法,用于求解较大规模的旅行商问题(Traveling Salesman Problem,TSP)。文献[4-5]针对TSP求解问题,设计了基于MapReduce技术的并行遗传算法,并分析了不同节点下的计算加速比。Hu等[6]针对利用大规模传感器网络进行实时水污染源的识别问题,设计了基于MapReduce技术的小生境并行遗传算法,并验证了算法优秀的计算性能。杨婉婧等[7]为提高BP神经网络算法的运行效率,提出了基于MapReduce的遗传算法用于BP神经网络的并行化设计及实现方法。
在以上研究成果的基础上,本研究提出了将MapReduce技术用于求解复杂物资调度及配载问题的多目标遗传算法的具体部署方法及改进策略。
1 考虑多种约束的物资调度及配载问题及多目标遗传算法实现
本研究以文献[8]所述物资调运及配载问题为研究对象,采用基于优先编码的两阶段多目标遗传算法(Two-Stage Priority-Based Multi-Objective Genetic Algorithm,TSPB-MOGA)为基础算法进行分析。本部分仅介绍其基本问题及TSPB-MOGA算法的核心算子。
1.1 问题简述及分析
如图1所示,战时或应急情况下指挥部门需根据物资储备信息和可调用的运输力量信息,结合物资需求单位(即需求点)所处地理位置与当前交通状况,以单位物资需求为基本条件,以平均送达时间最短、途中损失最小和平均车辆重量和容量利用率为目标,制定多个物资储备库(即供应点)直接向多个需求点进行物资保障的详细调度计划,以解决每个供应点应分别向谁配送、配送什么、配送多少、用什么配送和物资如何装车的问题。
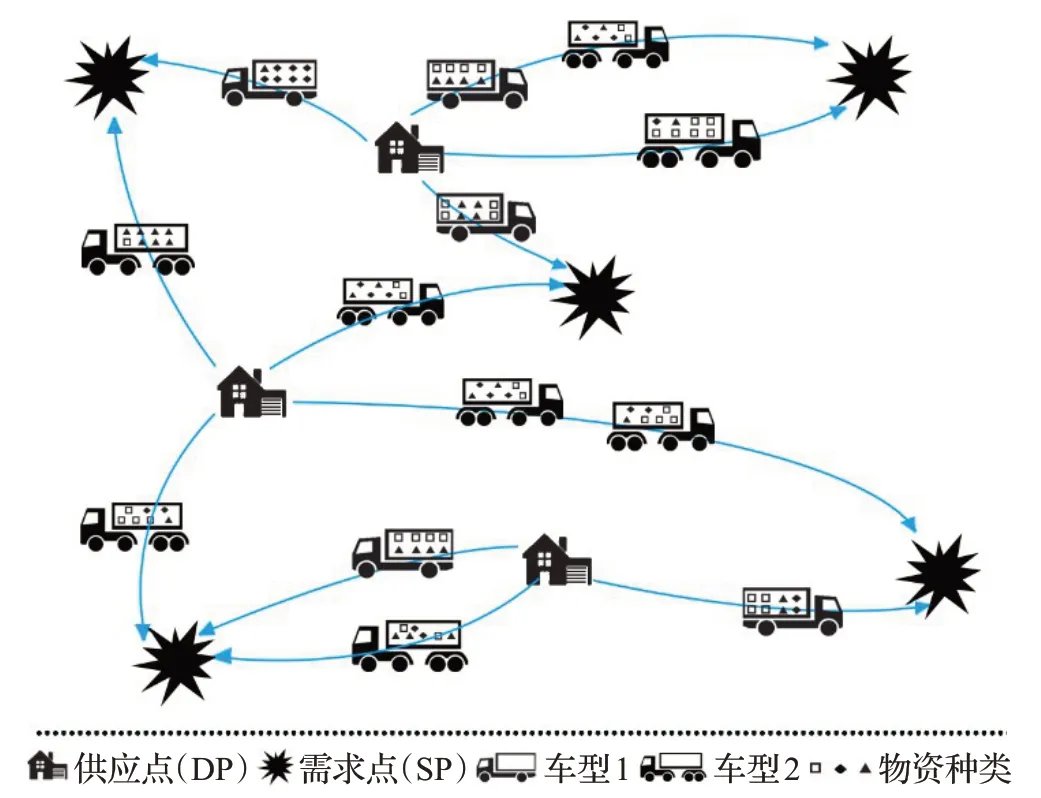
图1 物资调运及配载的基本实施过程
1.2 TSPB-MOGA求解算法
文献[8]在Gen等[9]利用遗传算法求解运输问题的研究基础上,设计了TSPB-MOGA算法对上述物资调运及配载问题进行求解,该算法流程框图如图2所示。
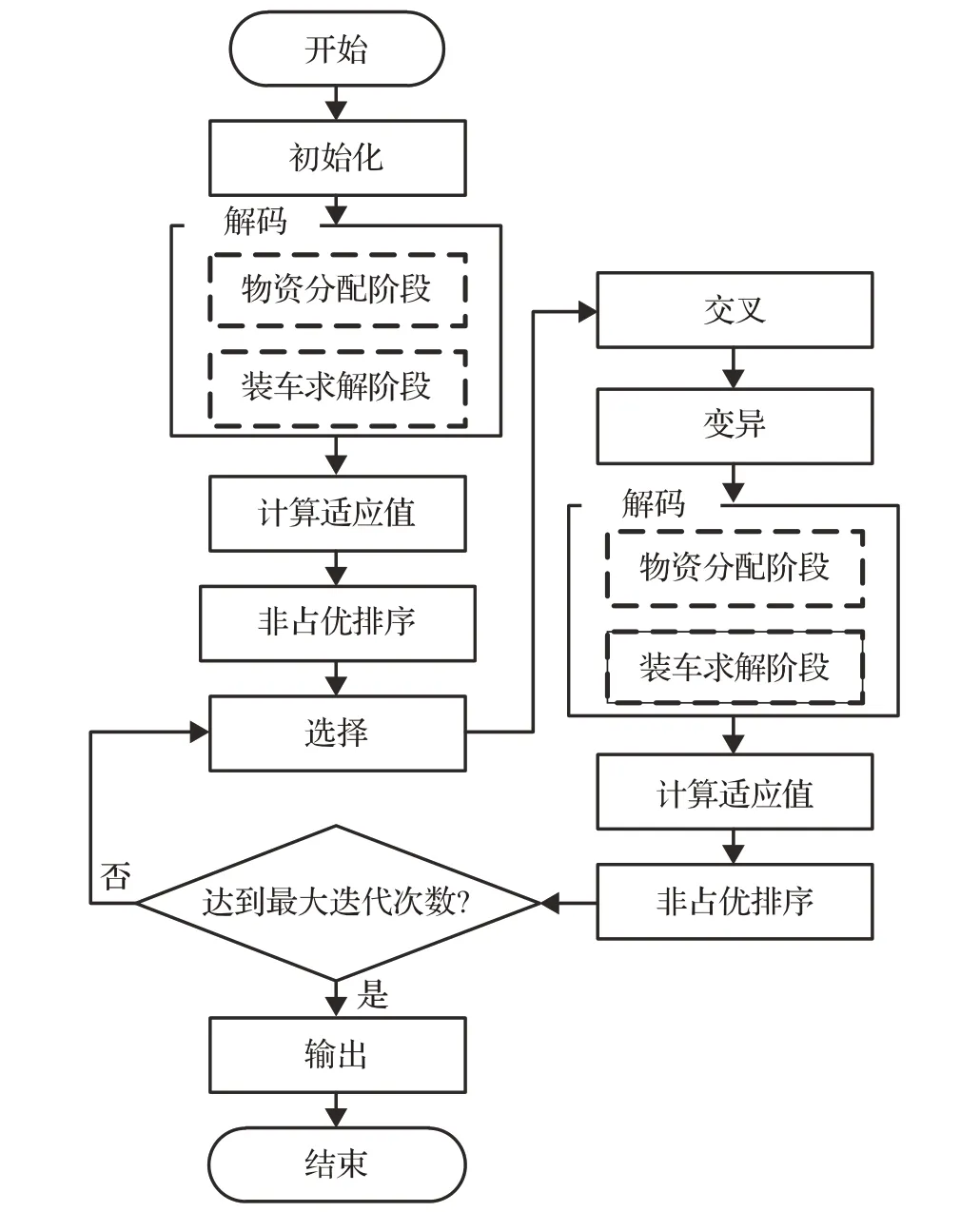
图2 基于优先编码的两阶段多目标遗传算法流程框图
(1)编码
算法采用供需节点总数+1的自然数顺序编码,其基因值代表供需节点的编号,基因位置代表供应点或需求点的保障顺序。比如,对于拥有3个供应点和5个需求点的物资调运网络,染色体“7 9 8 3 6 4 1 5 2”表示位于编码首位的第7个节点(即第4个需求点)有最高的物资保障优先权,位于编码次位的第9个节点(即第6个需求点)拥有第二优先权。
(2)解码
解码的目的是翻译和解释每条染色体所代表的物资调运方案(即物资由谁送、向谁送、送什么、送多少和如何装车的具体问题)。算法解码过程包含两个阶段:
第一阶段:基于优先保障序列的物资分配过程。此阶段对应图2中的“物资分配阶段”,提出了基于最大满足和非占优排序的物资分配算法,以全局配送时间最低和风险最低为目标为每个物资供应点提供详细的物资分配计划(不涉及物资配载优化)。
第二阶段:面向装载利用率最大化的物资配载。此过程对应图2中的“配载求解阶段”。该阶段的重点是获得详细的物资配载计划(对于各供应点而言,就是决定每辆车辆上应该配载各类物资的数量及其运往目的地)。
(3)交叉算子
设计采用面向优先保持的单点交叉算子[8]。
2 TSPB-MOGA算法在云计算环境下的设计
鉴于TSPB-MOGA算法具有较高的复杂度,而云计算技术具有很高的计算性能和运算可靠性,因此可对TSPB-MOGA算法利用MapReduce技术进行并行化编程和改进,形成基于MapReduce的TSPB-MOGA算法(MapReduce for Two-Stage Priority-Based Multi-Objective Genetic Algorithm,MPTSPB-MOGA),该算法具有并行运行、多目标求解、粗粒度模式和高可靠性等特点。
2.1 总体运行过程
图3是MPTSPB-MOGA算法的流程框图(为简化流程,本流程框图未对计算过程中的HDFS分布式文件存储和读取过程进行展示)。如图所示,遗传算法的并行化计算总体上是通过Hadoop各集群中的PC来协同完成的,在这一过程中,MapReduce主要起到了任务管理与并发计算的作用。首先,在初始化过程中读入相关数据并完成种群初始化;在Splitter过程中将种群分为多个相对独立的子种群(Islands)并传输于相应的Mapper;Map过程是实现遗传算法并行化的核心步骤,该过程可承担具有大量计算需求的计算任务,所有Mapper将同步完成各子种群个体的解码、适应值计算、非占优排序和新的子种群个体产生;Shuffle是汇总计算结果并重新分配个体到Reducer的过程;在Reducer中,若满足继续迭代的条件,各Reducer将完成所负责的所有个体间的交叉及变异任务,并执行各子种群间的个体迁移,准备进行下一次MapReduce的过程,若迭代终止,则根据相关条件筛选出当前的Pareto最优解并完成输出。

图3 MRTSPB-MOGA算法流程图
2.2 主要流程模块功能及实现方法
图3 中各主要流程模块的功能及实现方法介绍如下。
(1)初始化和Splitter
该初始化过程除需完成数据读入、参数设置外,还需按顺序地将种群存储于分布式文件系统HDFS中。Splitter的主要作用是将种群分割为P个子种群,并完成各个体的映射。此外,Splitter还会将各目标函数适应值的计算式也一并添加到各个Mapper中。
(2)Map过程
Map过程是该算法的核心,是实现并行计算的关键。在此过程中,位于各个Mapper的子种群并行、独立地实现所有个体的解码、适应值计算、非占优排序和子代种群的产生。鉴于各子种群会顺序执行解码和适应值计算等遗传算子,因此本文考虑采用Hadoop技术的ChainMapper和ChainReducer类[10]来实现多个Mapper的串行执行。
(3)Shuffle
总的来说,Shuffle就是完成整理并输出的过程,是将Map过程中所得结果进行汇总、排序等操作,然后按照设定规则传向Reducer的过程。而作为Shuffle过程的重要组成内容,Partitioner负责将结果分发传送到各个Reducer,是实现各Reducer负载均衡的关键。默认情况下,Partitioner会将指定key值的键值对送往指定的Reducer,但在遗传算法中,随着迭代的进行,种群逐渐向Pareto前沿靠近,这导致大量键值对被送往同一个Reducer而造成负载失衡。此外,由于具有相同或类似显性的个体大量聚集于相同的Reducer,这势必会影响迭代的性能,造成收敛速度大大降低。最后,Partitioner的默认设置为子种群的相对独立的进化过程造成了阻碍。为避免这种情况的发生,本研究设定Partitioner为固定对象分配模式,如图3所示,将Mapper所得结果固定地分配于与其对应的Reducer,使各MapReduce过程能完整保持位于不同集群的各子种群能独立地进化,直至达到最大迭代次数。
(4)Reduce过程
因为TSPB-MOGA算法的交叉和变异操作的计算复杂度和计算资源需求相对较低,所以将其放在Reduce阶段完成。当然,如图3所示,在此过程中还有一个迭代结束的条件判断符。若已达到遗传算法的最大迭代次数,则不再进行交叉和变异操作(也不再进行后续的种群迁移),将位于各集群的子种群进行汇总,进行Pareto最优解集筛选。
(5)迁移过程
通过各子种群间的个体迁移,相对独立和封闭的子种群得以完成遗传信息的交换和流动,该过程促进了种群的多样性,扩大解的搜索空间的同时提升了收敛速度。如图4所示(图中蓝色实心点代表个体,灰色椭圆代表子种群),本研究采用环形迁移的方法。为加快收敛速度,应加大种群间的迁移率,特别是优势个体的迁移,但迁移率的加大势必增加各种群(计算节点)间的通信开销。如图5所示,各子种群在进行迁移前,可参照NSGA II算法的思想[11]按照Rank优先、拥挤距离其次的顺序对各子种群的个体进行排序,将排序靠前的占优群体和靠后的劣势群体(数量为迁移率×子种群数量)迁移至下一个子种群,并按同样方法将下一个子种群的占优群体和劣势群体迁移至另一个子种群,最终实现全部子种群的个体迁移。

图4 环形迁移过程示意图

图5 环形迁移过程示意图
(6)Pareto最优解汇集
此过程的主要任务是将位于各计算节点的子种群的Pareto最优解汇集到一个独立的单机节点,对汇集后的种群重新进行非占优排序,并输出最终的Pareto最优解。
3 案例计算及分析
为详细说明MRTSPB-MOGA算法的综合性能,下面将从计算耗时、收敛情况、种群多样性保持和并行计算能力等角度分别介绍采用不同运行环境和运行架构的多库物资协同调运算法。
3.1 TSPB-MOGA在单机环境下的计算性能
设置算法的种群数量为pop=100,最大迭代次数maxgen=90,交叉概率p c=0.7,变异概率pm=0.25。算法采用Matlab 2015b编程并运行于装有Win7系统(64 bit),配置2.33 GHz的4核处理器和4 GB内存的PC上。
程序经过20次运行,平均耗时639.7(s均方差25.6 s),其中各主要算子的耗时占比如图6所示。从图中可以看出,该算法的解码过程约占计算总耗时的98.7%(分析可知,造成该算子耗时过多的主要原因在于对其的多次调用以及算子本身的计算复杂度),而适应值计算、非占优排序、交叉、变异等算子所耗费的计算资源之和不足2%(计算耗时不足10 s)。因此TSPB-MOGA算法具备并行化部署的基本特征。
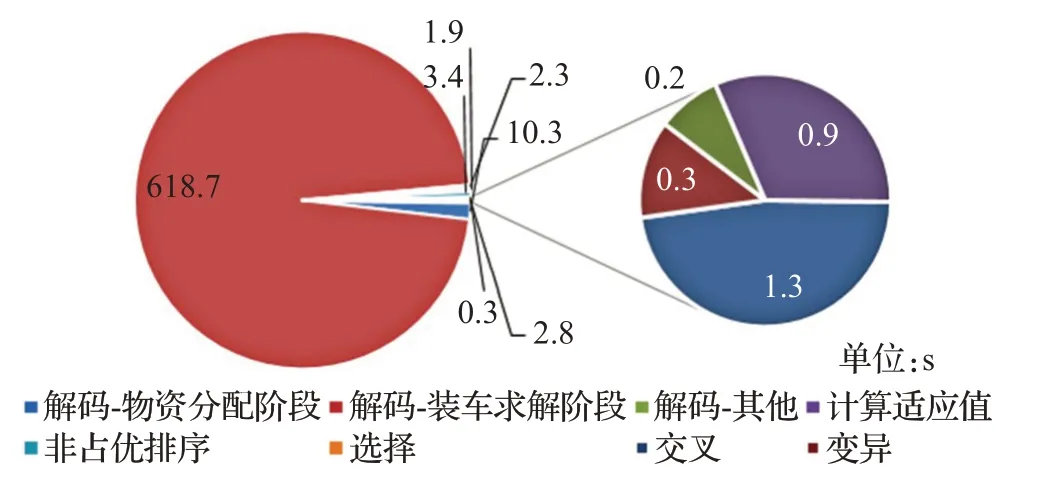
图6 各遗传算子耗时占比图(TSPB-MOGA)
3.2 MRTSPB-MOGA在Hadoop环境下的计算性能
(1)部署环境及参数介绍
虽然Hadoop可部署于Windows或Linux等系统环境下,但目前技术条件下Windows平台上的部署需借助Cygwin等模拟软件虚拟Unix系统。因此,本文考虑直接在Linux系统下部署Hadoop系统。实验环境由6台配置相同的PC搭建,每台PC的主要软硬件配置信息如表1所示。

表1 单机配置信息
MapReduce的过程是一个相对较为复杂的过程,集群通信、数据读写和后台资源调度占有不可忽略的时间消耗(文献[6,12-14]均已证实),因此MRTSPB-MOGA算法参数的选择应考虑减少集群通信和频繁数据读写的占比。设计MRTSPB-MOGA算法的主要参数如表2所示。设置较大的种群总量的原因在于加大单次迭代的计算量,提高有效计算的时间占比;子种群的数量等于种群总量与CPU数量的比值(均匀分配原则);迁移率(mr)是进行迁移的个体与子种群数的比例,一般情况下,迁移率越高,通信消耗越高,但算法收敛性能越好;迁移间隔为2表示算法每迭代两次,进行一次迁移,较低的迁移率有利于通信频率的降低。
(2)时效性分析
时效高低是衡量分布式计算算法性能的主要指标。本研究对以下4组实验进行了对比分析:(1)TSPBMOGA算法的串行执行。采用表2中的主要参数,将其运行于单机串行环境下。(2)MRTSPB-MOGA算法的伪分布式并行执行。采用MRTSPB-MOGA算法的运行环境(表1所示),但采用单机运行和串行执行的方式,只设置一个Mapper和一个Reducer。(3)MRTSPB-MOGA算法的分布式执行(有3台PC的集群)。这是真正意义上的MRTSPB-MOGA算法执行,只是在较小的集群规模下(6个Map-Reduce过程)。(4)MRTSPB-MOGA算法的分布式执行(有6台PC的集群)。不同环境下的算法运行耗时如图7所示。
总的来说,MRTSPB-MOGA算法能取得较好的加速比(相比于串行执行的TSPB-MOGA算法,6核和12核下的算法加速比达到了1.77和2.61)。此外,从图7可知,伪分布式并行执行的算法时耗远大于串行执行的情况,这是由于采用了Hadoop的GFS系统和MapReduce架构的原因,文件的频繁读写和MapReduce协调过程是造成这一耗时增加的主要原因。通过6核集群并行计算,将单个Mapper的计算负载分担于6个Mapper,实现了真正意义的分布式计算,使计算耗时大幅下降。没有使得计算耗时成Mapper数量下降的原因在于PC间通信、GFS文件系统读写、MapReduce过程中任务的协调和同步带来的时间消耗或延迟。
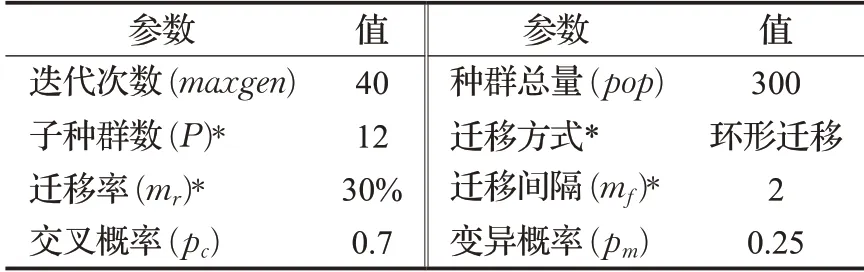
表2 MRTSPB-MOGA主要参数设置

图7 算法在不同运行环境下的耗时对比
(3)迭代性能对比
为跟踪和验证MRTSPB-MOGA算法的迭代性能,本文对TSPB-MOGA算法和MRTSPB-MOGA算法迭代过程中的Pareto前沿演变情况进行了对比研究。图8为初始种群(iter=1)、中期种群(iter=maxgen/2)和末代种群(iter=maxgen)的Pareto前沿的分布及进化情况。图中加注“MR”符号的为MRTSPB-MOGA算法所得的结果,图8(a)为Pareto前沿三维视图,图8(b)~图8(d)为平面视图。从图中可知,尽管进行了分布式架构的改造并采用了子种群间个体迁移的方式弥补多样性的保持,但MRTSPB-MOGA算法仍取得与TSPB-MOGA相似的迭代性能(图中前沿解具有较高重合度),特别是从图8(a)和图8(b)中可以看出,MRTSPB-MOGA取得了更为靠前的Pareto前沿。
(4)求解结果分析
TSPB-MOGA算法和MRTSPB-MOGA算法采用大体相同的多目标遗传算法核心算子(包括编码、解码、适应值计算、交叉、变异和选择等),区别主要在于算法运行环境和是否采用基于MapReduce技术的并行化处理,因此,在最终求解结果上具有近乎相同的体现,图8也正好验证了这一推断。
4 结束语
本研究结合云计算的MapReduce技术,对物资调运算法及部署进行了较为深入的研究。实验证明,MRTSPBMOGA算法具有更为优异的求解性能,对其他并行算子有高耗时的遗传算法的改进或性能提升有一定借鉴意义。
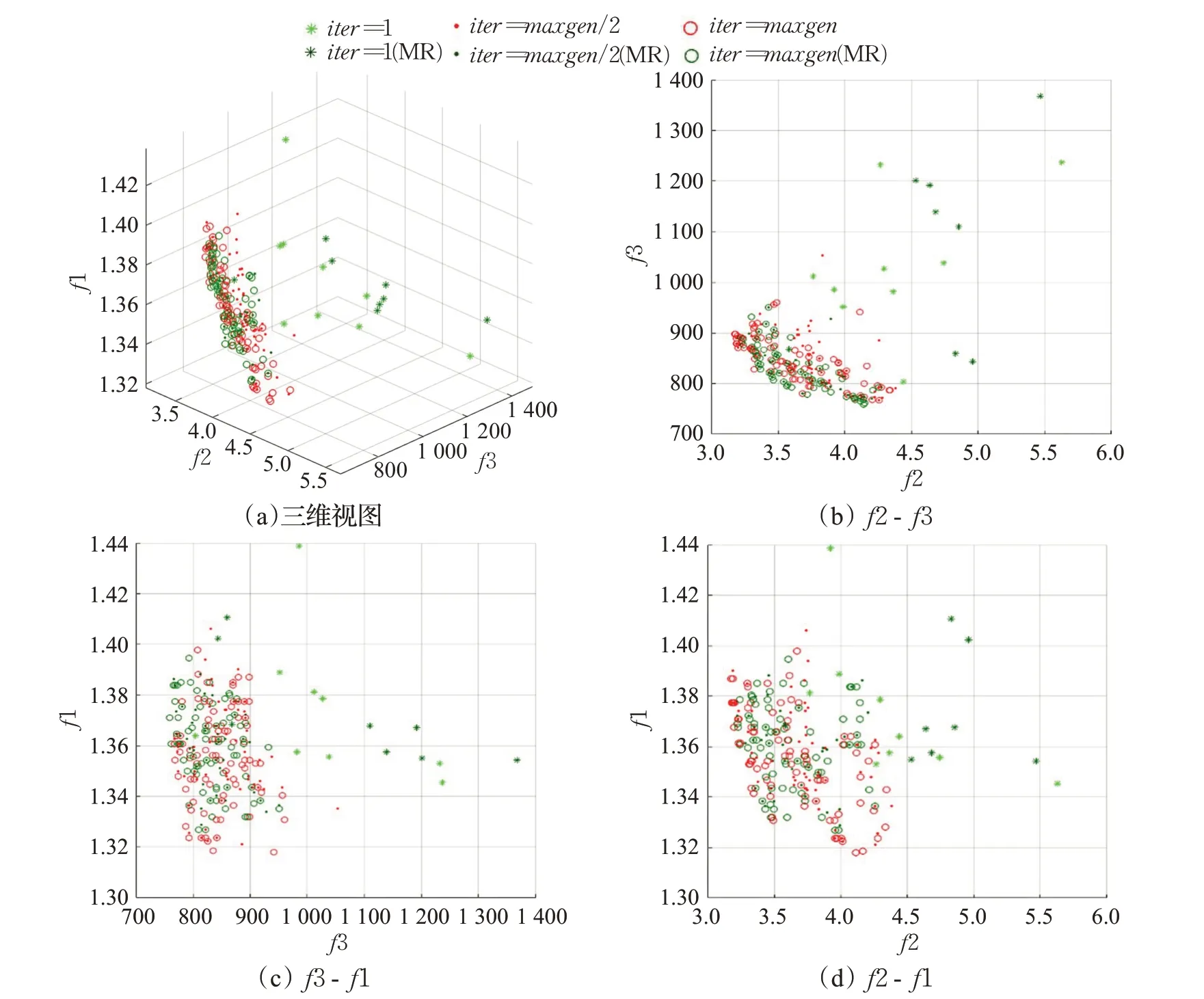
图8 TSPB-MOGA和MRTSPB-MOGA算法Pareto前沿演变对比图

