改进A*算法在路径规划中的应用
王保剑,胡大裟,蒋玉明
1.四川大学 计算机学院,成都610065
2.四川省大数据分析与融合应用技术工程实验室,成都610065
随着中国制造2025的不断推进,对我国工业制造的智能自动化提出了更高的要求。智能自动化仓库系统作为现代工业制造的基础,因此成为智能系统研究的热点领域之一。其中基于自动导引车(Automated Guided Vehicle,AGV)的智能自动化仓库系统是智能仓库系统的重要分支。在由多台自动导引车组成的自动导引车系统(Automated Guided Vehicle System,AGVS)的运行过程中,需要解决任务调度、路径规划和避碰等一系列问题[1-3],其中AGVS的路径规划是研究的热点、难点。
目前主要路径规划算法有Dijkstra算法[4]、A*算法[5-6]等,智能路径规划算法有蚁群算法[7]、遗传算法[8]、Q-learning算法[9]等。其中A*算法是启发式搜索算法[10],其算法本身具有简洁高效,能够快速找到最优解的优点,因此被广泛应用于AGVS路径规划。A*算法有很多局限性,文献[11]提出一种结合跳点搜索算法的改进A*算法,能够有效减少列表中无用节点数量,减少计算量,提高算法效率,解决A*算法在规模较大的AGVS中对多个AGV进行路径规划的应用场景中系统开销大,路径规划速度慢的问题。文献[12]在当前节点的启发函数中加入父节点的启发函数,使启发函数在代价函数中的占比保持在一个合理范围,提高算法的实时性。文献[10]采用新的数据结构将A*算法中的搜索操作并行化,同时实现算法的快速插入操作,提升算法的效率。文献[13]在传统A*算法的启发函数中引入网路负载,能够有效均衡各网络负载,改善出口区域负载过高的情况。但是采用模型较为简单,只考虑特殊情形下局部网络负载过高的情况,与实际应用场景差别较大,改进算法并不能广泛适用于AGVS的路径规划。
AGV寻路过程中避开高负载节点是解决局部拥塞的关键。因此本文在传统A*算法的启发函数中,引入节点负载,从算法层面上解决了多AGV系统采用传统A*算法进行路径规划时容易造成局部节点负载过高的问题,从而避免AGV系统陷入局部拥塞,提高系统效率。最后通过模拟仿真实验,证实了改进算法的可行性。
1 问题描述
本文改进A*算法是应用在基于栅格地图[14]的智能仓库,智能仓库模型如图1所示。仓库模型主要有以下部分:
(1)分拣台:用于存放待分拣的货物,AGV执行任务的起点,位于仓库模型的最左侧。
(2)道路:位于分拣台和货架之间,用于AGV搬运货物。
(3)货架:集中在仓库模型的中间靠右侧,用于存放已经分拣好的货物。
(4)AGV:用于货物搬运的工具,能够根据相应的算法,把货物从起点运送到目标节点位置。

图1 智能仓库模型图
以模型构建的现实性和易处理性为原则,不失一般性[15],提出如下假设:
(1)结合智能仓库的实际应用情况AGV的运动方向只考虑上下左右,可横向或纵向跨越栅格[16]。
(2)不考虑AGV的装载和卸载时间,即AGV的装载和卸载时间均为0。
(3)AGV运行过程中速度不变,不考虑起始点出发时加速,到达目的地减速的过程。
(4)不考虑包裹到达投递区之后的出库过程。
(5)单个AGV只能搬运单个货物,一个货物也只能被一个AGV搬运。
(6)为了最大程度上避免冲突和死锁,本文采用文献[17]的避碰策略,任务优先级高的AGV先行,优先级低的AGV则等待。
2 A*算法
2.1 算法描述
A*算法是一种启发式搜索算法,引入了最优启发式函数,可以在搜索过程中避免盲目性[18],其表达式如式(1):

其中,AGV路径是由各个节点组成,可通过节点集合{d1,d2,…,dn,…,dm}表示,d1表示起始节点,dn表示为当前节点,dm表示目标节点。f*(n)为代价函数,g*(n)是起始节点到当前节点的最短距离,如果g*(n)=0,代价函数所表示的算法是最佳优先搜索算法(BFS)。h*(n)是当前节点到目标节点的最短距离,如果h*(n)=0,代价函数所表示的算法是Dijkstra算法。目前是无法通过该节点预知该节点与目标节点的最短距离,因此使用h(n)代替h*(n),因此替换过后的代价函数表达式如式(2):

h(n)选取原则为h(n)的值不大于h*(n),通常使用欧式距离计算公式、曼哈顿距离计算公式和切比雪夫距离计算公式,其对应表达式分别是式(3)~(5):

2.2 算法流程
A*算法流程的核心就是维护Open和Closed两个集合。其中Closed集合中存放的是已拓展节点,Open集合中存放待拓展节点。节点代价函数值表示该节点的优先级,选取Open集合中代价最小(优先级最高)的节点进行拓展,将已经拓展的节点存放在Closed集合中。如果目标节点出现在Open集合中,则依次返回父节点,最终规划出一条路径。其算法的路径规划过程如图2。
其中橙色节点D1为路径的起点,Dm为目标节点,黑色节点为障碍物,AGV无法通过障碍物节点,绿色节点为待拓展节点,白色为可通过节点。最终生成一条蓝色节点的路径。
2.3 传统A*算法不足之处

图2 A*算法寻路过程示意图
在采用传统A*算法的多AGV系统中,代价函数只考虑起始节点到当前节点的最短路径和当前节点到目标节点的最短路径估计。在很多应用场景中,AGV起点相对集中在一个区域,目标节点相对集中在另一个区域。若是采用传统A*算法,只考虑距离作为单一评价方式的启发函数,执行不同任务的AGV所行走的路径大致相同,这会导致一部分节点繁忙,一部分节点空闲。繁忙节点负载较大,周围常常有多个AGV需要竞争、抢占该节点,因此该节点周围会出现等待或滞留的AGV,容易导致该区域出现局部拥塞甚至是死锁。同样系统中的很多空闲节点就会造成资源的浪费,系统效率低下。多AGV抢占节点如图3所示。

图3 多个AGV抢占节点示意图
图中,箭头表示AGV移动的轨迹,灰色节点表示有多个AGV抢占的节点。然而在传统A*算法的启发函数中,没有引入节点负载,因此无法在寻路过程中避开这些高负载节点,避免局部拥塞的发生。
3 结合节点负载的改进A*算法
本文提出一种结合节点负载的改进A*算法,在传统A*算法的启发函数中引入节点负载,并且提出动态节点负载计算公式,能够动态更新节点负载,有效提高算法的实时性。改进算法的表达式如式(6):

其中,n表示寻路过程中拓展的第n个节点,f(n)是代价函数表示待拓展节点的优先级,f(n)值越大,节点优先级就越低,f(n)值越小,节点优先级就越高。g(n)是起始节点到当前节点的最短距离,l(n)是结合节点负载的节点启发函数,μ是一个常数,对节点负载进行缩放,使算法有更好的表现,如果μ=0,该算法就变成传统的A*算法,h(n)是传统A*算法的启发函数,常用曼哈顿距离或者欧式距离计算公式。k n是此时第n个节点的负载值,存储在一个(M×N)的二维矩阵中,通过维护二维矩阵,动态更新节点负载值,负载值最低是0,其计算公式如式(7)、(8):
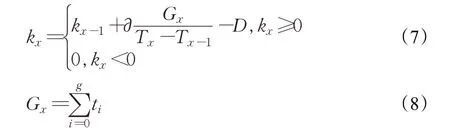
其中,x表示节点负载迭代次数,k x表示第x次迭代过后的节点负载值,T x表示第x次迭代的时刻,迭代从T0时刻开始,并且T0…T x时间间隔相等,∂是一个系数,G x表示T x-1~T x这段时间内所有通过该节点的AGV所花费的总时间,其计算公式如式(8)。g表示T x-1~T x这段时间内通过该节点的AGV数量,t i表示第i个AGV通过该节点花费的时间。D是节点冷却常数,如果T x-1~T x这段时间没有AGV或者有较少的AGV通过该节点,该节点负载就会相应减少,系统每隔T x-T x-1更新一次二维矩阵,并且节点负载值恒大于等于0。
本文提出的改进A*算法,在启发函数中引入节点负载作为评价函数,从而节点负载影响AGV寻路过程中节点的选择。如果节点负载较高,其相应的代价函数f(n)就会较大,对应的优先级就会较小,因此AGV在寻路过程中就会优先考虑负载较低的节点,从而均衡各个节点的负载,达到避免局部拥塞的发生,提升系统效率的目的。
中国—东盟博览会永久落户南宁,不仅为南宁吸引了大量的外部投资,也为南宁的旅游业带来了充足的客源。因此,中国—东盟博览会在推动南宁经济的同时,也使南宁旅游业整体质量的提高。东博会和旅游业的良性互动,使得两者融合发展,促进南宁城市竞争力。在中国—东盟博览会的影响下,南宁的旅游业不断向好向快发展;而南宁旅游业的完善也在一定程度上保证了东博会举办的质量。两者的互动迎来社会和谐发展共赢的局面。
4 仿真实验
4.1 环境模型
实验采用栅格地图对智能仓库模型进行建模,将本文提出的改进A*算法与基于交通规则下的A*算法[19]做对比,证明改进算法能够有效均衡各节点负载,提高系统效率。仿真模拟规则如下:
(1)生成20×20的栅格地图,每个格子长1 m,小车的速度1 m/s。其中灰色方格表示分拣台,为每个AGV分配货物,黑色格子表示货架,AGV执行相应的任务将分拣台上的货物运输到指定货架,黑色小圆点表示正在执行任务的AGV,白色格子表示AGV可以通行的区域。栅格地图如图1。
(2)对应地图生成和维护两个二维矩阵和一个系统时钟记录时刻T x,从T0时刻开始,并且T0…T x间隔相等。第一个矩阵用于存放公式(8)计算出T x-1~T x时间段内所有通过该节点的AGV所花费的总时间。再通过公式(7)计算生成对应的节点负载值并存放在第二个二维矩阵。每隔∆T(T x-T x-1)更新一次二维矩阵,时间间隔∆T设为8 s。其中,节点负载最大值为40。
(3)AGV系统生成150个任务,使用不同数量的AGV分别使用基于交通规则下的A*算法,改进算法完成任务,对应的AGV数量依次是5、10、15、20、25、30。记录系统完成所有任务所需要的时间,AGV行走的总路程和不同时间段节点负载值。
4.2 算法对比
仿真系统分别采用基于交通规则的A*算法(简称算法1)和本文的改进A*算法(简称算法2)进行对比实验,分别记录AGV系统完成所有任务的总时间,单个任务完成的平均时间,AGV行走的总里程和节点负载,从不同维度对算法1和算法2进行对比。
图4所示的是在分别采用算法1和算法2的AGV系统中,完成150个任务所需要的时间。蓝色实线表示算法1,橙色虚线表示算法2。从图中不难发现,随着系统中AGV数量的增加,系统所花费的时间会相应减少。当系统中AGV数量超过15个时候,两种算法都趋于缓和,但算法2优于算法1,总的系统消耗时间比算法1减少了16.18%。

图4 AGV系统完成任务总时间
图5 所示的是拥有不同AGV数量的AGV系统完成单个任务所需要花费的平均时间。随着系统中AGV数量的增加,完成单个任务的平均时间增加。当系统中有较多AGV时,多个AGV抢占节点的概率增加,根据公式(7)、(8),被抢占节点负载增加,从而被抢占节点所在区域中会出现多个AGV等待下一节点释放或一直未能抢占到下一节点而滞留父节点的现象,使得该区域节点负载增加,导致局部拥塞,甚至死锁,大大降低系统效率。算法2在寻路过程时能够有效避开高负载节点,对比算法1能够减少14.24%的时间开销。

图5 完成单个任务的平均时间
图6 所表示的是在AGV系统中,完成所有任务AGV行走的总里程。在采用算法1进行路径规划的AGV系统中,随着系统中AGV数量的增加,AGV行走的总里程变化较小,维持在一个特定值附近。然而在采用算法2的AGV系统中,AGV行走总里程随着系统中AGV数量的增加而相应增加,在算法1的基础上增加了4.67%。这是因为改进算法在算法1的代价函数中引入节点负载,AGV在寻路过程中会避开高负载节点,没有选择最短路径,牺牲了路径长度,减少时间开销,提高了系统效率。

图6 AGV移动总里程
表1对比了算法1和算法2的节点负载情况,系统中AGV数量为30,时间是系统开始运行后80 s。算法2虽然平均负载值相对算法1增加了5.45%,但标准差减少了-29.93%,说明改进算法能够有效避开热点节和利用低负载节点,均衡各节点负载。

表1 节点平均负载和标准差表
5 结束语
本文提出一种结合节点负载的改进A*算法,在启发函数中引入节点负载,对比基于交通规则下A*算法,虽然增加了系统中AGV行走的总路程和节点平均负载,却换了更少的时间开销,以及提高了单个任务的执行效率。通过仿真实验能表明改进A*算法能够有效避开高负载节点,均衡各节点负载,避免局部拥塞,提高系统运行效率。

