定数截尾场合三参数pareto分布参数的最优置信区间
刘 璐, 李云飞
(西华师范大学 数学与信息学院, 四川 南充 637009)
0 引言
Pareto分布是研究收入模型的一种分布,经过不断发展,由两参数pareto分布推广到三参数pareto分布和广义pareto分布.Pareto 分布在社会经济、军事以及可靠性统计分析等很多领域中得到广泛的应用[1].因此,研究 pareto 分布,尤其是研究其参数估计问题,具有重要的理论意义和实用价值.
关于pareto分布参数的最优置信区间,许多专家和学者对其进行了研究,已经形成了丰富的研究成果.Neyman[2]的理论,在给定置信水平,以保证有一定的可靠度下,精度往往用区间长度来衡量,区间长度越短说明对参数估计得越准确.Ali等[3]提出了一种推导广义pareto分布形状参数统计检验的一般方法,并证明了这种方法优于经典的极大似然比检验.Singh等[4]利用最大熵原理,提出了三参数广义pareto分布参数估计一种新的方法.佟毅[5]研究并给出了定数截尾下指数分布平均寿命参数和平均失效率参数的最优置信区间,通过算例分析并得出了小样本场合下用最优置信区间作为未知参数的置信区间更好.王娟等[6]给出Pareto分布中尺度参数的几种区间估计方法,重点研究之前不常见的极大似然估计的渐近正态性法和轮廓似然函数法,并说明这几种方法的适应范围及优缺点.徐美萍等[7]通过对比weibull分布尺度参数的最短置信区间和常用置信区间,发现研究小样本情形时参数最短置信区间的重要性和必要性.王芳等[8]将两参数的pareto分布情形推广到了三参数,并研究了尺度参数和形状参数估计的渐进性质.刘荣玄等[9]在逐步增加首失效截尾样本下,研究了三参数pareto分布族形状参数的一致最小方差无偏估计.秦祖启等[10]讨论了枢轴量服从F分布,而F分布的密度函数是极不对称的,基于此两正态分布方差比优化后的置信区间.蔡洁等[11]用最优假设检验的统计量构造出两正态总体方差比的枢轴量,并从最短置信区间的本质意义出发,构造出求解最短置信区间的条件和证明出其解的存在唯一性,得出用最短置信区间作为方差比的区间估计,精度将会得到显著提高.刘璐等[12]通过构造置信区间的一个枢轴量的方法,求定数截尾场合Pareto分布形状参数的最短置信区间,并将其与传统方法求得的置信区间进行对比分析得出最优置信区间.
本文将在定数截尾寿命试验场合下,针对三参数pareto分布单总体参数的最优置信区间和两总体形状参数比的最优置信区间进行研究.
1 单总体尺度参数σ的置信区间
若随机变量X服从三参数Pareto分布,其密度函数和分布函数分别为
f(x;σ,θ,μ)=θσθ(x-μ)-(1+θ),x>σ+μ,
(1)
F(x;σ,θ,μ)=1-σθ(x-μ)-θ,
(2)
记为X~Pareto(θ,σ,μ),其中θ>0为形状参数,σ>0为尺度参数,μ∈R为位置参数,并假设为已知常数.
抽取来自总体Pareto(θ,σ,μ)的容量为n的一个样本X1,X2,…,Xn,当有r个样品失效时停止寿命试验,失效数据为X(1)≤X(2)≤…≤X(r).
1.1 用枢轴量法求σ的最短置信区间
定理1设T1,T2,…,Tn是来自双参数指数分布总体E(δ,θ)的容量为n的样本,定数截尾数是r,T(1)≤T(2)≤…≤T(r)是前r个次序统计量,则:
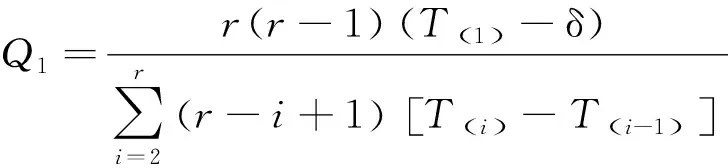
证明令H1=rT(1),Hi=(r-i+1)[T(i)-T(i-1)],i=2,3,…,r,则H1,H2,…,Hr相互独立,且H1~E(r,δ,θ),H2,H3,…,Hr同分布于E(θ),那么H1-rδ,H2,…,Hr独立同分布于E(θ),则:
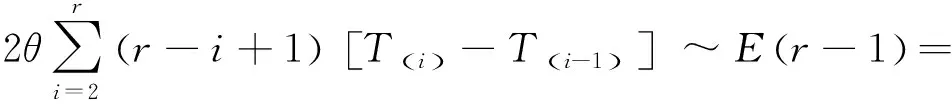
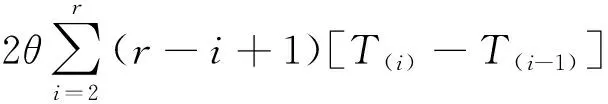
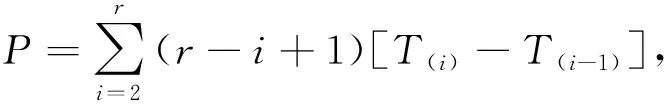
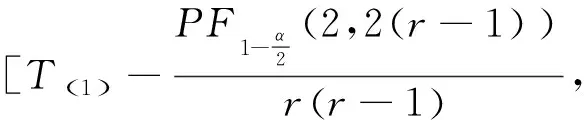
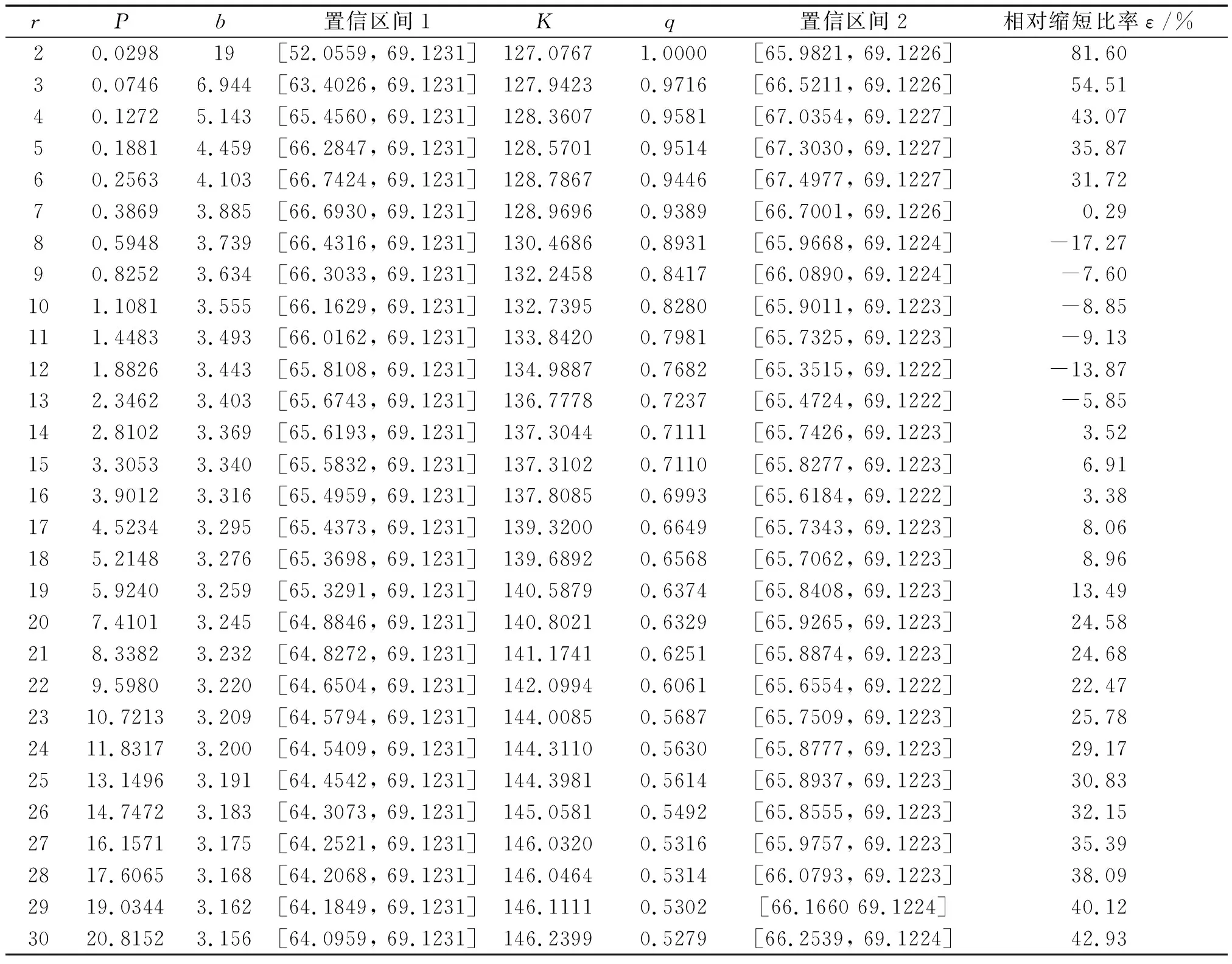
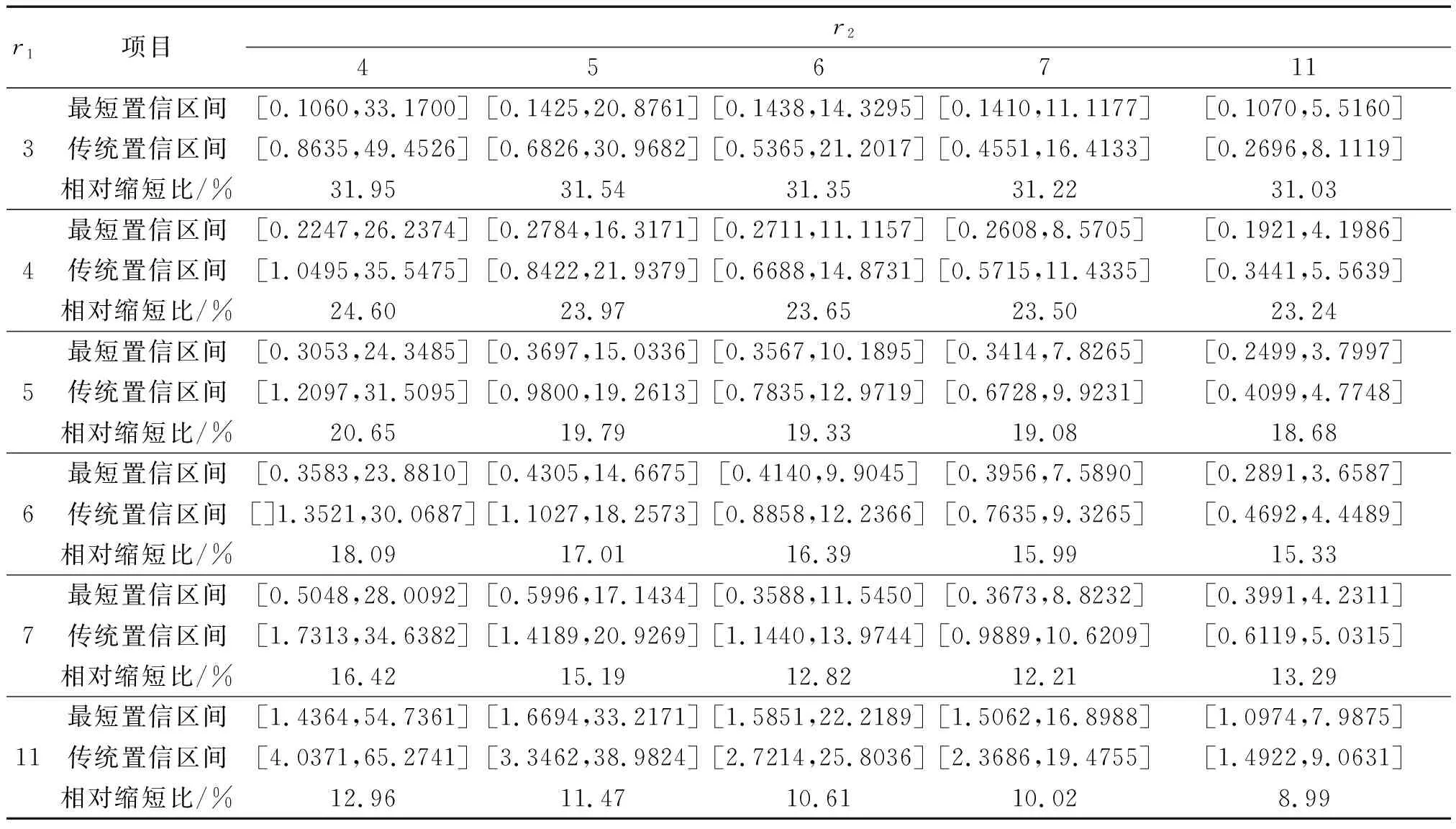
为了求δ的最短置信区间,假设存在a,b(0 此时δ的置信区间为: 这个区间的平均长度为: 定理2当α0=0时,δ的置信度为1-α的最短置信区间为: 设h(α0)=b-a,则 (3) 其中 因为总体Pareto(θ,σ,μ)含有三个参数,而现在只对尺度参数σ进行估计,所以可以通过轮廓似然函数法求其置信区间. 令η=(θ,σ,μ)Τ,根据(1)和(2)得η在定数截尾寿命试验下的似然函数为: 从而η的对数似然函数为: (4) (5) 要使lnL(xi,η)取得最大值,则σ的极大似然估计为: (6) θ的极大似然估计为: (7) 由(4)式可以得到参数σ的轮廓似然函数为: 将(5)式代入lnpL(xi,η)中得到: 又因为参数σ的偏差度函数为: 将(6)和(7)代入上式得到: 所以,对于给定的α∈(0,1),构造σ的置信区间: (8) 定理3设X1,X2,…,Xn1是来自总体Pareto(θ1,σ1,μ1)的样本,Y1,Y2,…,Yn2来自总体Pareto(θ2,σ2,μ2)的样本,两个总体相互独立.对它们做定数截尾寿命试验后,得到失效数据分别为:X(1)≤X(2)≤…≤X(r),Y(1)≤Y(2)≤…≤Y(r),其中θ1,σ1,θ2,σ2均未知. 分别令T=ln(X-μ1),Z=ln(Y-μ2),则: 证明令T=ln(X-μ1),Z=ln(Y-μ2),则fT(t;δ1,θ1)=θ1e-θ1(t-δ1),其中δ1=lnσ1;fY(y;δ2,θ2)=θ2e-θ2(t-δ2),其中δ2=lnσ2.根据定理1的证明,同理可得: ~F(2(r1-1),2(r2-1)). 因为Q2的分布F(2(r1-1),2(r2-1))是已知的,且此分布与θ1,θ2无关.故将Q2作为枢轴量来构造形状参数比θ2/θ1的置信区间.因为枢轴量服从F分布,F分布的概率密度函数非对称分布,利用分位数 构造的传统置信区间 就并非θ2/θ1的最短置信区间.其中 为了求θ2/θ1的最短置信区间,假设存在φ1,φ2满足0<φ1<φ2,使得: 此时θ2/θ1的置信区间为: 这个区间的平均长度为: 当r1=2时,F(2(r1-1),2(r2-1))分布的第一自由度≤2,其密度函数为单调递减,θ2/θ1的置信度为1-α的最短置信区间为: 成立,其中g2(x)为F(2(r1-1),2(r2-1))分布的概率密度函数,那么 (9) 为θ2/θ1的最短置信区间. 利用Matlab软件可以用随机模拟的方法产生一个总体为X~Pareto(θ,σ,μ)的截尾样本,具体步骤如下: 1)产生一个容量为n=30且服从均匀分布U(0,1)的独立同分布样本T1,T2,…,Tn; 2)当σ=b时,给定参数θ=a和μ=c,其中a,b,c均为不等于零的常数. 假设产品的寿命服从形状参数为θ1=2.22、尺度参数为σ1=68和位置参数为μ1=10的pareto分布,现在从这批产品中随机抽取n1个样品进行定数截尾寿命试验.当n1个样品中出现第r1个失效时,所得到的寿命数据(小时)按照从小到大的顺序排列如下: 当r1=1时,X1=79.1231; 当r1=2时,X1=79.1231,X2=81.2175; 当r1=3时,X1=79.1231,X2=81.2175,X3=82.2896; … 当r1=30时,X1=79.1231,X2=81.2175,X3=82.2896,X4=82.8524,X5=83.4619,X6=84.0014,X7=88.7709,X8=95.0987,X9=97.0298,X10=101.7209,X11=107.1334,X12=116.7245,X13=119.8929,X14=119.9307,X15=123.4077,X16=135.4312,X17=138.7833,X18=148.0011,X19=150.4866,X20=155.3181,X21=169.4068,X22=207.0749,X23=214.668,X24=217.2301,X25=241.3268,X26=291.0766,X27=292.0871,X28=298.2338,X29=317.4058,X30=342.9619. 给定置信水平为1-α=0.95,以下通过算例分析给出尺度参数的最优置信区间.具体算例结果如表1所示,其中置信区间1表示运用枢轴量法求得的尺度参数σ1的最短置信区间;置信区间2表示运用轮廓似然函数法求得的尺度参数σ1的置信区间;相对缩短比率ε%表示置信区间2的长度比置信区间1的长度相对缩短百分比. 表1 尺度参数的置信区间的精度分析 从表1中可以看出:对于定数截尾三参数pareto分布,当2≤r≤7和r≥14时,轮廓似然函数法所求得σ1的置信区间比枢轴量法求得的最短置信区间更优;当8≤r≤13时,枢轴量法所求得σ1的最短置信区间比轮廓似然函数法求得的置信区间更优. 在3.1的基础上再进行寿命试验,假设产品的寿命服从形状参数为θ2=4.20,尺度参数为σ2=128和位置参数为μ2=25的pareto分布,现在从这批产品中随机抽取n2=30个产品进行寿命试验.当n2个样品中出现第r2个失效时所得到的寿命数据(小时)按照从小到大的顺序排列如下: 当r2=1时,X1=153.9897; 当r2=2时,X1=153.9897,X2=154.0728; 当r2=3时,X1=153.9897,X2=154.0728,X3=154.4488; … 当r2=30时,X1=153.9897,X2=154.0728,X3=154.4488,X4=156.1522,X5=156.9200,X6=158.5244,X7=159.4624,X8=160.9591,X9=163.2322,X10=163.2730,X11=165.1679,X12=166.3306,X13=168.5161,X14=171.8702,X15=172.2997,X16=175.2410,X17=175.8502,X18=182.8402,X19=188.9387,X20=189.9235,X21=192.8554,X22=194.8000,X23=196.3208,X24=196.7846,X25=203.8605,X26=205.7937,X27=211.7149,X28=218.4335,X29=286.4805,X30=300.0382. 给定置信水平为1-α=0.95,以下通过算例分析给出两总体形状参数比的最优置信区间.具体算例结果如下表所示: 因为,对于F(2(r1-1),2(r2-1))分布,当第一自由度r1≥3时,其密度函数才为单峰非对称.由于篇幅的问题,这里只考虑r1=3,4,5,6,7,11,r2=4,5,6,7,11时,两总体形状参数比的置信区间. 表2 形状参数比θ2/θ1置信区间的精度分析 从表2可以看出固定r1的取值时,随着r2的取值不断增大,最短置信区间下边界值不断增大(φ1的取值不断增大),最短置信区间上边界值不断减小(φ2的取值不断减小),形状参数比的置信区间的精度越来越高;同时还可以看出,两种方法算得的置信区间的长度随着r2的增大差异越来越小,缩小的速度也越来越慢.因此,在样本容量较小时,形状参数比的最短置信区间即为最优置信区间. 利用“枢轴量”和“轮廓似然函数”两种方法,求出了定数截尾场合下三参数pareto分布单总体尺度参数σ的置信区间,通过算例分析的结果,得到当2≤r≤7和r≥14时,轮廓似然函数法所求得σ的置信区间比枢轴量法求得的置信区间更短,所以此时用轮廓似然函数法求得的置信区间即为最优置信区间;当8≤r≤13时,枢轴量法求得的置信区间长度更短,这时用枢轴量法求得的置信区间即为最优置信区间.然后,根据枢轴量法得到了两总体形状参数比θ2/θ1的最优置信区间,由于容易构造形状参数比θ2/θ1置信区间所需的枢轴量,且枢轴量所服从分布的密度函数曲线是单峰非对称,在样本容量较小时,用最短置信区间作为目标函数得到的置信区间比按传统概率对称方法求得的置信区间更优,参数估计精度也得到显著提高.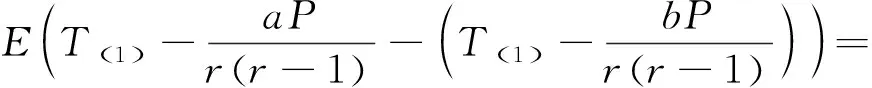


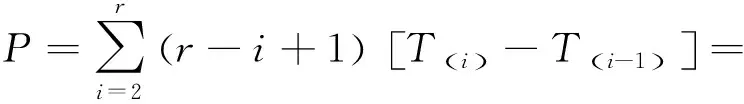
1.2 用轮廓似然函数法求σ的置信区间
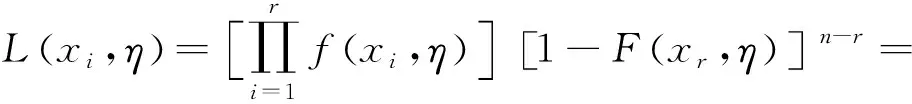



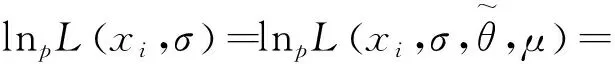
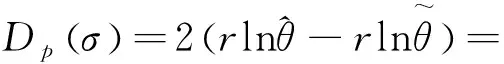
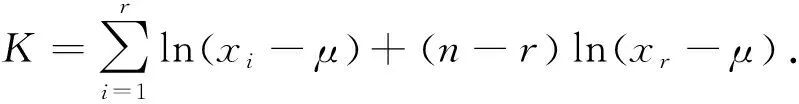
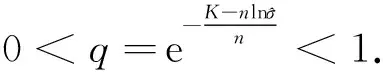
2 两总体形状参数比θ2/θ1的置信区间
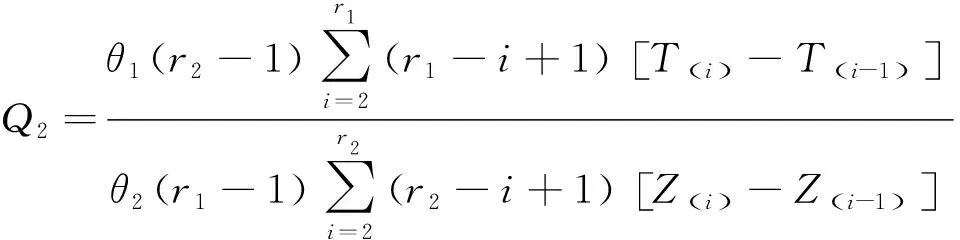
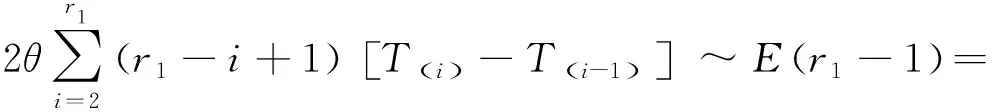
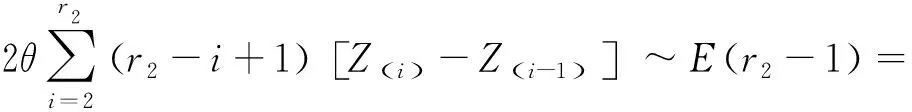
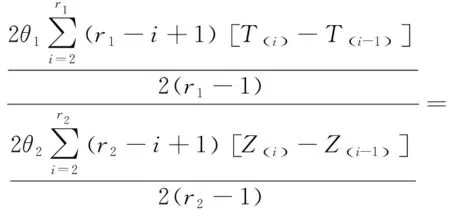
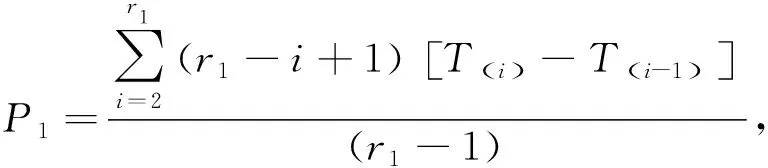
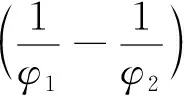
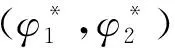
3 算例分析
3.1 随机模拟
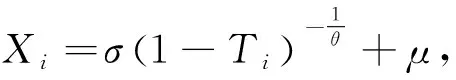
3.2 单总体定数截尾下对比枢轴量法和轮廓似然函数法所求得σ的最优置信区间
3.3 两总体定数截尾下形状参数比θ2/θ1的最优置信区间
4 结论

