两种平方损失下反向帕累托分布形状参数的E-Bayes估计
蓝 海, 徐 宝
(吉林师范大学 数学学院, 吉林 四平 136000)
0 引言
在Bayes统计推断中,先验分布和损失函数的选取是最为重要的环节之一.常用的损失函数有:平方损失函数、加权平方损失函数、LINEX损失函数、熵损失函数.文献[1]使用平方损失函数得到可靠度Bayes估计;文献[2]在加权平方损失函数下研究了幂函数分布参数的Bayes估计与性质;文献[3]利用LINEX损失函数对手术工具标定理论与实验;文献[4]在LINEX损失函数下估计指数种群的位置参数;文献[5]在加权p,q对称熵损失函数下给出了pareto分布形状参数的最小风险同变估计;文献[6]使用加权广义熵损失函数研究了Weibull模型的贝叶斯可靠性.
选取先验分布时往往都会带入新的参数,进而影响了估计的效果,为了减小新参数对估计的影响,文献[7]提出了一种新的参数估计法——“E-Bayes估计法”.基于该估计法的优点,大量学者都相继使用该估计法来对参数进行估计.如:文献[8]带应用的Weibull分布可靠性特征的E-Bayes估计;文献[9]非对称损失函数下指数Lomax分布的E-Bayes估计;文献[10]威布尔模型的E-Bayes和多层Bayes估计比较;文献[11]认为威布尔分布无失效数据的E-Bayes估计是可靠度的估计;文献[12]逆高斯分布形状参数的E-Bayes估计;文献[13]在Mlinex损失函数下得到了几何分布的E-Bayes估计.
本文在第一节中给出反向帕累托分布在位置参数已知时,形状参数在加权平方损失函数下的E-Bayes估计.在第二节中给出了形状参数在平方损失函数下的E-Bayes估计.在第三节中通过随机模拟验证了本文所使用的方法的合理性且E-Bayes估计的仿真性较高.其中反向帕累托分布的密度函数和分布函数分别为
f(x)=αθ-αxα-1;0
F(x)=θ-αxα;0
α为形状参数,θ为位置参数,简记RP(θ,α).加权平方损失函数和平方损失函数的表达式分别为
(1)
L2(α,δ)=(δ-α)2,(α>0).
(2)
1 加权平方损失函数下的E-Bayes估计
在Bayes统计推断中,随着先验分布的选取往往会添加新的参数,为了减小这些新参数对估计的影响,有学者提出了E-Bayes估计.本节首先列出E-Bayes估计的定义,然后结合定义讨论RP(θ,α)分布中的形状参数α在损失函数(1)下的E-Bayes估计.

由定义可以看出:为了求出形状参数α在损失函数(1)下的E-Bayes估计,首先需要求出参数的Bayes估计,因此下面将在Bayes理论框架下,讨论参数α的Bayes估计,进而求出α的E-Bayes估计.
定理1.1设X1,X2,…,Xn为来自RP(θ,α)分布的样本观察值,记X=(X1,X2,…,Xn),在损失函数(1)下,对于任意的先验分布,形状参数α的Bayes估计为
证明设δ(X)为参数α的任一估计,在损失函数(1)下,δ(X)的Bayes风险为
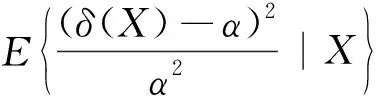
δ2(X)E(α-2|X)-2δ(X)E(α-1|X)+1,
所以将上式关于δ求微分并令其为零,便可得到极值点
又因为该极值点是其唯一的极小值点,所以形状参数α的Bayes估计为
定理1.2设定RP(θ,α)分布的形状参数α的先验分布为Γ(β,γ),其中参数β,γ为超参数,且β>0,γ>0,则在损失函数(1)下,形状参数α的Bayes估计为
证明因为形状参数α的先验分布为Γ(β,γ),则有
又因为RP(θ,α)分布的密度函数为f(x)=αθ-αxα-1;0
因此形状参数α的后验密度为
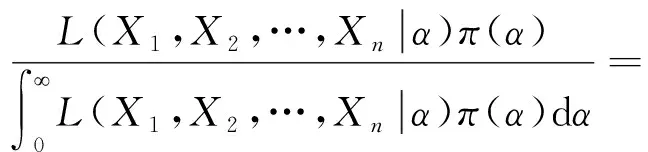

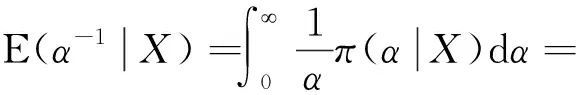
同理可得
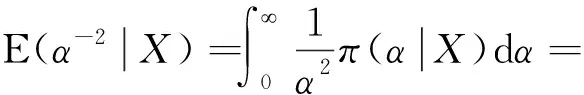
因此由定理1.1易知,α的Bayes估计为
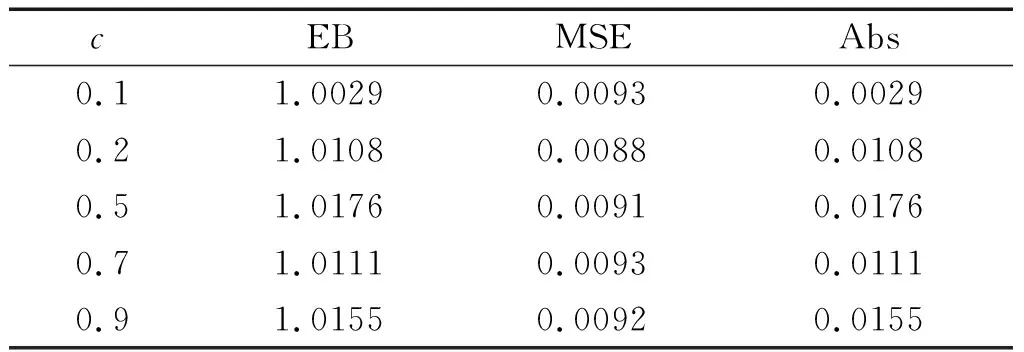
接下来将在先验分布为Γ(β,γ)下讨论形状参数α在损失函数(1)下的E-Bayes估计.根据文献[15],为了使估计的效果较好,参数β和γ的取值应使先验分布密度函数为参数α的减函数.再根据文献[16],考虑估计的稳健性,最终确定0<β<1,0<γ 定理1.3RP(θ,α)分布中的形状参数α在损失函数(1)下的E-Bayes估计为 证明首先由定理1.2可知,参数α在损失函数(1)下的Bayes估计为 本节将研究RP(θ,α)分布在位置参数θ已知时,基于损失函数(2)探讨形状参数α的E-Bayes估计. 定理2.1设X1,X2,…,Xn为来自RP(θ,α)分布的样本观察值,记X=(X1,X2,…,Xn),在损失函数(2)下,对于任意的先验分布,形状参数α的Bayes估计为δB*(X)=E(α|X). 证明仿照定理1.1的证明过程即可证明,因此这里从略. 定理2.2设定RP(θ,α)分布的形状参数α的先验分布为Γ(β,γ),其中参数β,γ为超参数且β>0,γ>0,则在损失函数(2)下,形状参数α的Bayes估计为 因此由定理2.1可知,α的Bayes估计为 定理2.3RP(θ,α)分布中的形状参数α在损失函数(2)下的E-Bayes估计为 证明由定理2.2可知,参数α在损失函数(1)下的Bayes估计为 为了验证本文所使用的方法的合理性以及估计的精确性,本文通过MATLAB进行随机模拟.设定θ=1000,α=1,c=1.其中EB表示形状参数α的E-Bayes估计,MSE表示估计的均方误差,Abs表示偏差的绝对值.模拟结果见表1、表2,表中的结果均为模拟结果的平均值. 表1 加权平方损失函数下EB估计的模拟结果(θ=1000,α=1,c=1) 表2 平方损失函数下EB估计的模拟结果(θ=1000,α=1,c=1) 由表1和表2的模拟结果可以看出,无论是在损失函数(1)还是损失函数(2)下,当样本容量增大时E-Bayes估计的MSE和Abs都在减小, 说明估计量具有大样本性质.在损失函数(1)下的E-Bayes估计的值随着样本容量的增大逐渐递增地接近真值,而在损失函数(2)下的E-Bayes估计的值随着样本容量的增大逐渐递减地接近真值,并发现当样本容量为n=100时,模拟效果最好.因此接下来在样本容量固定为100时,改变c的值进行随机模拟.由于考虑估计的稳健性c的值分别取为c=(0.1,0.2,0.5,0.7,0.9).模拟结果见表3、表4. 表3 加权平方损失函数下EB估计的模拟结果(θ=1000,α=1,n=100) 表4 平方损失函数下EB估计的模拟结果(θ=1000,α=1,n=100) 由表3至表4的结果可以看出,在损失函数(1)下的E-Bayes估计的值要比在损失函数(2)下的E-Bayes估计更靠近真值,因此在研究RP(θ,α)分布的形状参数时,选取损失函数(1)相比损失函数(2)效果较好.还发现在不同损失函数下,形状参数α的E-Bayes估计的MSE和Abs都较小且精度较高,因此可在此基础上对RP(θ,α)分布形状参数α进行更深入的研究与探讨. E-Bayes估计法有效地改善了存在于先验分布中的新参数对估计的影响,鉴于该估计法的优点以及目前反向帕累托分布的理论研究较少,本文在位置参数已知时讨论了反向帕累托分布的形状参数分别在加权平方损失函数和平方损失函数下的Bayes估计和E-Bayes估计,并通过模拟计算验证了E-Bayes估计的合理性,在一定程度上丰富了对于反向帕累托分布的理论研究.

2 平方损失函数下的E-Bayes估计


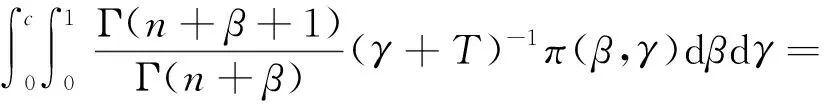
3 模拟计算



4 结束语

