中学数学教学中不可轻视的函数结构

安徽省马鞍山市第二中学郑蒲港分校 陶尚明

安徽省马鞍山市第二中学 刘向兵

在很多次的教学研讨或者公开课中，经常听到教师们称二次函数为基本初等函数，甚至也有的教师很诧异“为什么指数函数会被称为超越函数？”本文将结合运算与解析式谈函数的分类与这两者的联系，给教师备课提供更多的素材，希望能够促进数学教学。

一、运算与解析式

在研究函数分类之前，很有必要了解一下“代数”这门学科。代数是研究数与字母的关系、性质和运算法则的分支学科，是研究实数和复数以及以它们为系数的多项式的代数运算理论和方法的数学分支学科。解方程就是代数的一部分内容，而初等代数的中心内容就是解代数方程，在中学，我们以研究初等代数为主。要讨论代数方程，首先遇到的一个问题是如何把实际问题中的数量关系列成带有未知数的代数式，然后根据等量关系列出代数方程，所以初等代数的一个重要内容就是代数式。那么，代数式与本文中的函数分类究竟有什么样的联系呢？带着疑问，我们先从运算谈起。

1.运算

2.解析式

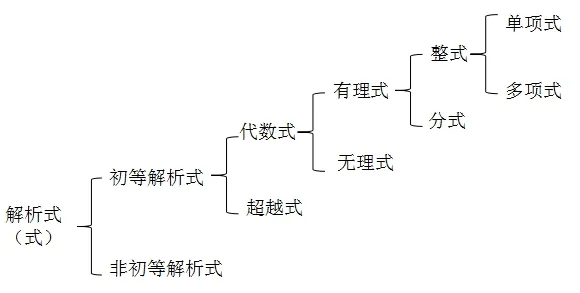
图1

二、函数相等

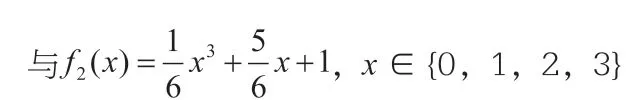
我们一起回顾一下《普通高中数学课程标准实验教科书·数学》中关于函数的定义：“如果两个函数的定义域相同，并且对应关系完全一致，我们就称这两个函数相等。”从教材的这段叙述来看，函数相等的定义很明确：如果函数的定义域和对应法则相同，那么函数相等。笔者同意第二种观点，对应法则本质就是自变量与因变量的配对法则，解析式只是一种表示方式，式的形不同，配对的法则不一定不同，如果表达式可以化简或者等价到同一种形式，那么对应法则就是一样的，这与代数中的式（也叫解析式）不一样，其强调的是形，而函数注重对应关系的本质。例子中的两个函数定义域一样，定义域中每一个数所对应的函数值都是完全一致，如图2，因此这两个函数相等。函数的实际配对没有区别，像这样的两个函数不应该被分成两类不同的函数。

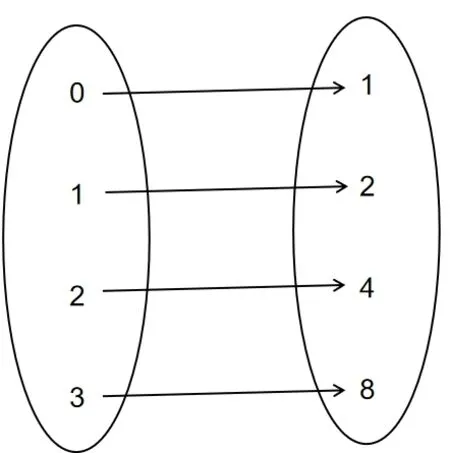
图2

三、函数分类

1.基本初等函数与初等函数

关于基本初等函数的提法，各个文献有所不同，常见的有三种提法。第一种提法：基本初等函数包括常值函数、幂函数、指数函数、对数函数、三角函数与反三角函数六大类函数；第二种提法：基本初等函数包括幂函数、指数函数、对数函数、三角函数与反三角函数五大类函数；第三种提法：基本初等函数包括常值函数y=1、恒等函数y=x、正弦函数y=sinx以及指数函数y=ex这四个函数。先不讨论谁更优，那么怎么形成初等函数呢？文献提出由基本初等函数经过有限次四则运算及有限次复合步骤得到的函数称为初等函数。而第二种提法下，初等函数是由常数与基本初等函数经过有限次四则运算及有限次复合步骤得到的函数。其实第二种提法与第一种提法差距不大，无本质区别。文献中指出，如果是第三种提法，那么初等函数则是由基本初等函数经过数乘、有限次四则运算、有限次复合步骤及求反函数而得到的函数。目前主流说法是第一种提法，之所以是第一种提法，笔者认为有多方面因素，如对数的出现是数学历史上关于数的重大发明，一要突出其地位，二要尊重历史，三是能够让中学生更直接地了解数学中最经典的知识。而且为了给学生减负，很多知识在现有的中学阶段已经淡化，如数乘与反函数，中学教材中仅仅是在平面向量中提及数乘运算，且在学习指对函数时简单提了一下反函数，甚至反三角函数直接不提。以上是笔者自己的观点，不太成熟，有误欢迎指正。

2.初等函数与非初等函数

由于函数注重对应关系的本质，根据运算（与对应法则相对应），可以将函数分为初等函数与非初等函数，至于每一种函数的名称与函数表达式在这里不再详述，如图3是函数的结构分类。

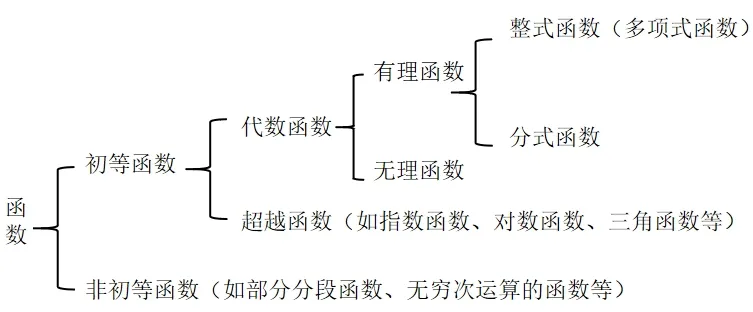
图3

本文有很多是笔者在教学过程中发现的问题，加入了很多自己的观点，由于水平有限，不当之处，希望专家或读者批评指正，只求能够解决疑惑和达成共识。虽然本文中函数的结构分类不是中学数学教学的重点，但是至少能给读者在中学数学教学时提供更加完整的备课素材，同时科普一下数学文化知识，这就达到了笔者写这篇论文的初衷了。