探究教学贵在生成*——以“点到直线的距离”探究性教学为例

刘亚平 刘全生 陈庆来 (江苏师范大学附属实验学校 221011)

孙琳琳 王 强 (江苏省丰县中学 221700)

“探究教学法”就是以某个或某一类相似问题为载体，以探究为方式，以四基(基础知识、基本技能、基本思想、基本活动经验)为举措，以提升学生数学核心素养为目的的一种教育教学方法．通过高一、高二的数学学习，高三学生已经逐步掌握了必备的知识框架和方法体系，对解决数学问题方法的选择及思想的优劣有了一定的甄别能力，不再仅仅满足于教师的“讲授”，学生的“听受”等以教师为主导的教学模式，迫切寻求以“教”为重心向以“学”为重心的学习方式的转换，这就需要教师根据学生思维发展的需求审时度势地调整教学方法．探究性学习是学生由“学会”转化为“会学”的一种重要的自主学习模式．下面笔者以一节高三数学“点到直线的距离”探究性教学为例，谈谈对实施探究教学法的一些举措与思考，以期抛砖引玉．

1 教学过程

“上节课后老师给同学们布置了一节‘点到直线的距离’的研究性学习课，大家可以把研究过程的所见、所闻、所思、所惑，畅所欲言地表达出来，与同学们一起分享探究历程中的收获与快乐．”教师的话刚说完，就有学生说出藏在心中已久的困惑.

1.1 寓教于乐，让学生有话可说

问题1苏教版数学必修2[1](第102页)在推导点到直线的距离公式时，主要给出两种方法：第一种方法是分四个步骤推导点到直线的距离公式．第一步求直线DE斜率，第二步求直线DE方程，第三步求直线DE与直线AB的垂足，第四步求两点D,E的距离；第二种方法运用三角形等面积法推导点到直线的距离公式．方法2的确巧妙且运算量较小，但不容易想到；方法1虽然运算复杂，但是容易想到啊而教科书却话锋一转：方法1运算量较大，下面我们通过构造三角形，利用面积关系求点D到直线AB的距离．我感觉教科书做法有些舍本逐末，是不是我们以后遇到复杂的计算或推理，就一定要寻找其他的计算或推理的“巧法”呢？学生1的“诉求”引起共鸣，同学们跃跃欲试、摩拳擦掌，很快推出点P(x0,y0)到直线l:Ax+By+C=0的距离公式．过程如下：

师生共同反思方法1有三个闪光点：第一，思路自然；第二，方法可行；第三，操作可控．教育家爱默生曾指出：“教育成功的秘诀在于尊重学生．谁掌握了这把钥匙，谁将获得教育上巨大的成功．”在数学教学过程中，教师要倾听学生的心声和困惑，关注学生的想法，以便及时调整教学方向，做到有针对性地讲解．在上课伊始，教师就没有想到学生会质疑教材，提出问题1，看到学生由于收获喜悦而欢呼雀跃时，教师对自己的教学行为深感欣慰．如果忽视了学生对方法1的质疑，不仅仅是丧失了一次提高学生运算能力的契机，更是剥夺了学生学习数学的追求与信仰．

学习数学离不开解题，解题才是学习数学的心脏．大家能不能给出关于点到直线的距离公式的试题？有的学生翻书，有的学生查阅高考数学参考资料，有的学生上网搜寻相关试题，有的学生拿出早已写好试题的小纸片等，经过师生共同讨论、交流、筛选、梳理，给出如下的一系列层层递进、精彩纷呈的问题．

问题2求点P(1,1)到直线l:x-y-3=0的距离．

1.2 曲径通幽，使学生有事可做

问题3(2011年高考数学上海卷理科第23题)已知平面上的线段l及点P，任取l上一点Q，线段PQ长度的最小值称为点P到l的距离，记作d(P,l)．

(1)求点P(1,1)到线段l:x-y-3=0(3≤x≤5)的距离d(P,l)；

(2)设l是长为2的线段，求点的集合D={P|d(P,l)≤1}所表示的图形面积．

图1 图2

(2)由题意知，所求图形面积与线段l如何摆放没有关系，为了同学们便于观察，我们把线段l的两个端点分别放在E(-1,0),F(1,0)处．因为d(P,l)≤1，所以点P到线段EF上每个点都是以1为半径的圆面．通过观察可知，点P轨迹是一个边长为2的正方形和两个半径为1的半圆(包括内部的所有点，如图2)，所以点的集合D={P|d(P,l)≤1}所表示的图形的面积为4+π．

第(1)问通过直觉观察可以得到点P到点A的距离最小，再通过建立二次函数在特定区间上求最值得以证明；(2)先解决线段l的一个特殊摆放位置(如线段EF位置)所对应的图形面积，当线段l任意摆放时，只是把点P对应的图形——一个边长为2的正方形和两个半径为1的半圆(包括内部的所有点)跟着改变即可，显然面积仍为4+π．

在反思解题过程中，同学们逐渐认识到“大胆猜想、小心论证”的必要性与重要性．就在他们对此解法津津乐道之时，教师追问：同学们知道了点到线段的距离定义，那如何定义曲线到直线的距离？他们很快异口同声说：曲线C上的点到直线l的距离的最小值称为曲线C到直线l的距离．

问题4(2012年高考数学浙江卷理科第16题)定义：曲线C上的点到直线l的距离的最小值称为曲线C到直线l的距离．已知曲线C1:y=x2+a到直线l:y=x的距离等于C2:x2+(y+4)2=2到直线l:y=x的距离，求实数a的值．

图3

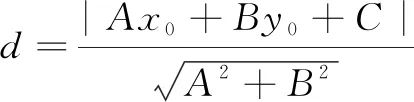
问题5(2017年高考数学上海卷第12题)如图4，用35个单位正方形拼成一个矩形，点P1,P2,P3,P4以及四个标记为“▲”的点在正方形的顶点处，设集合Ω={P1,P2,P3,P4}，点P∈Ω，过点P作直线lP，使得不在lP的“▲”的点分布在lP的两侧．用D1(lP)和D2(lP)分别表示lP一侧和另一侧的“▲”的点到lP的距离之和．若过P的直线lP中有且只有一条满足D1(lP)=D2(lP)，则Ω中所有这样的P为．

图4

心理学研究表明，一个人面临错综复杂的陌生情境时，难免都会有点心慌意乱，不过有的人会立刻回归平静，积极寻找解决问题的方案与对策．本题条件开放，涉及字母比较多，解题方向不明，是学生最惧怕的题型之一．这怎么办呢？教师可以先引导学生解决最简单的问题：如图5，ABCD是正方形，不妨设正方形的顶点A,B到直线l的距离之和等于顶点C,D到直线l的距离之和，试问直线l是否过某一定点？请说明理由．通过作图可知直线l一定通过正方形ABCD的中心O．学生运用合情推理不难猜出问题5中的直线lP一定过以“▲”为顶点的四边形的中心，即P2．

图5

图6

1.3 厚积薄发，助学生登高望远

经过学生的动手操作、亲身实践，同学们体会到点到直线、点到线段、曲线到直线的(有向)距离本质都是点到点的距离．通过抽象这三种距离概念的共同特征，可以衍生出意味深长的“曼哈顿距离”定义[2]：设X是一个非空集，X叫做距离空间，是指在X上定义了一个双变量的实值函数ρ(x,y)，满足下列三个条件：(1)ρ(x,y)≥0，而且ρ(x,y)=0，当且仅当x=y；(2)ρ(x,y)=ρ(y,x)；(3)ρ(x,z)≤ρ(x,y)+ρ(y,z)(∀x,y,z∈X)．

这里ρ叫做X上的一个距离，以ρ为距离的距离空间X记做(X,ρ)．由于曼哈顿距离背景新颖，形式灵活，能较好地考察学生的数学核心素养，所以备受高考数学命题专家的青睐．

问题6(2006年高考数学福建卷理科第12题)对于直角坐标平面内的任意两点A(x1,y1),B(x2,y2)，定义它们之间的一种“距离”：‖AB‖=|x2-x1|+|y2-y1|．给出下列三个命题：①若点C在线段AB上，则‖AC‖+‖CB‖=‖AB‖；②在△ABC中，若∠C=90°，则‖AC‖2+‖CB‖2=‖AB‖2；③在△ABC中，‖AC‖+‖CB‖>‖AB‖．其中真命题的个数为( )．

A．0 B．1 C．2 D．3

由于是客观题，只要取特殊情况，答案不难揭晓．如取A(-1,0),C(0,0),B(1,0)，可验证第1个结论正确；再取A(1,0),C(0,0),B(0,1)，可验证第2个结论与第3个结论皆错误，故答案选B．如果是解答题，只需证明第1个结论正确即可，设C(x3,y3)，因为点C在线段AB上，不妨设x1≤x3≤x2，y1≤y3≤y2，代入“距离”公式可以证明第1个结论成立，同理可证其他情况也成立．

无独有偶，2010年高考数学广东卷再次出现蕴涵更加深厚的“曼哈顿距离”试题．此试题以“曼哈顿距离”为载体，将解析几何的核心思想和绝对值性质、绝对值不等式、不等式证明等内容有机地联系起来，背景新颖但源于课本，因此符合学生的认知基础与认知能力，既体现了在知识交汇处命题的原则，又体现了高考命题的公平性原则，考查学生能否打破定势思维，换个视角观察问题、分析问题及解决问题的能力．

问题7(2010年高考数学广东卷理科第21题)设A(x1,y1),B(x2,y2)是平面直角坐标系xOy上的两点，现定义由点A到点B的一种折线距离ρ(A,B)为ρ(A,B)=|x2-x1|+|y2-y1|．对于平面xOy上给定的不同的两点A(x1,y1),B(x2,y2)．

(1)若点C(x3,y3)是平面xOy上的点，试证明：ρ(A,C)+ρ(C,B)≥ρ(A,B)；

(2)在平面xOy上是否存在点C(x3,y3)，同时满足①ρ(A,C)+ρ(C,B)=ρ(A,B)，②ρ(A,C)=ρ(C,B)．若存在，请求出所有符合条件的点；若不存在，请予以证明．

本题是含绝对值符号的证明题，可谓来势汹汹、咄咄逼人，再加上考试时间的紧迫，如果同学们是当年考生的话，大家也会感到沉重的心理压力(学生们频频点头表示认可)．大家要明白“题在书外，理在书内”的道理，遇到思维障碍要联想到书本的相关知识，点击脑海中相关的知识结构和方法体系的格点，激活和撷取相应的知识与方法，并联想相关的基本数学活动经验，探寻解题的切入点与突破口．在教师循循善诱的引导下，学生通过尝试逐渐明白：在解决每一个问题时都至少有六个绝对值符号，因此无法采用通过平方去掉绝对值符号，故本题实质是考查三角形绝对值不等式．

证明 (1)因为ρ(A,C)+ρ(C,B)=|x3-x1|+ |y3-y1|+|x2-x3|+|y2-y3|≥|(x3-x1)+(x2-x3)|+|(y3-y1)+(y2-y3)|=|x2-x1|+ |y2-y1|=ρ(A,B)，当且仅当(x3-x1)(x2-x3)≥0,(y3-y1)(y2-y3)≥0时取等号．

(2)结合第(1)问取等号条件，再运用分类讨论思想即可(以下教学过程略)．

2 教学思考

教育家赞可夫认为：“教学法一旦触及学生的情绪和意志领域，触及学生的精神需要，这种教学法就发挥高效的作用．”[3]笔者认为，探究教学法就是能触及学生情绪和意志领域、精神需要的一种行之有效的教学方法．随着新课改理念的逐步深入，以学生为主体的探究教学法备受数学教师的推崇，并取得了不错的教学成效，但还有一些肤浅的“伪”探究教学的现象，如何“去‘伪’存真”实施探究教学法？笔者认为要做好以下三点：

2.1 选择贴近学生思维实际的内涵丰富的问题是顺利实施探究教学法的基础

之所以有“伪”探究教学现象的发生，其中一个主要原因是由于探究问题选择不当造成的，如果探究问题过于简单，学生就会不探自明，探究就会流于形式；如果探究问题高不可攀，学生就会望而生畏，探究就会难以开展；如果探究问题内涵单一，学生就会索然无味，探究就会难以使学生意犹未尽．因此，教师要把好探究问题的质量关，探究问题可以从学生作业、考试中产生的共性错误、共性困惑或典型问题中选择，也可以从学生自主学习中感兴趣的、有价值的、有底蕴的问题中选择，还可以从数学学习中学生遇到的数学知识发生发展的生长点和衔接点、数学思想方法的转折点、数学思维的症结点等处选择[4]．

本节课中，教师首先从学生质疑教材能否运用四步骤推导出点到直线的距离公式开始，师生齐心协力、众志成城地解决困扰学生心中许久的困惑，遵循学生思维发展的规律，教师引导学生循序渐进地探究了点到线段距离、曲线到直线距离、点到直线的有向距离、曼哈顿距离等五彩缤纷、隽永含蓄的一系列问题．这些平面“距离”的问题系列兼顾基础性、多变性、生长性，反映了知识间的错综复杂、千丝万缕的内在联系，是培养学生创造性解决问题的绝佳素材．学生驰思遐想、开拓视野，研讨气氛热烈高涨又紧张有序．

2.2 培养学生观察问题、合情推理的能力是顺利实施探究教学法的保障

普通高中数学课程标准提出要培养学生发现问题、提出问题、分析问题、解决问题的能力，还倡导学生要学会用数学的眼光观察世界．目的是强调观察问题能力在学习数学中应该有一席之地．在普通高中课程标准实验教科书中，教材编者也煞费苦心地引导教师要注重对学生观察能力的培养．如学习函数的奇偶性、单调性、指数函数的性质等，都是先让学生观察一些函数图象，找出规律、看出端倪，然后再理性认知；再如学习直线与平面平行(垂直)的判定与性质定理，平面与平面平行(垂直)的判定与性质定理等，都是先让学生动手操作、仔细观察、直观感知、归纳猜想、理性确认，最后纳入新知．有些学生由于受定势思维的影响，总认为演绎推理是解决问题的“正道”，习惯用因为、所以逻辑链来解决问题，把合情推理放在了遗忘的角落．其实，合情推理是一种发散性思维，遇到新背景、新情境、新思想、新观点、新构想、新方法等问题时，通过合情推理可以发现一些结论，然后为下一步探索新问题提供新的研究起点与方向，这是演绎推理所无法企及的．

学生需要探究的问题往往都是其思维的困惑点、疑难点、拐角点，有时直接运用演绎推理从正面强攻硬取很难奏效，这就需要其运用观察问题、合情推理等能力来寻找解决问题的切入点与突破点．在解决问题5时，如果直接运用点到直线的距离公式求解，思路容易受阻，但通过对特殊情况细致入微的观察就会发现直线lP一定通过相应四边形的中心，再运用点到直线的有向距离公式把猜想的结论进行严谨的证明，学生便茅塞顿开，解决问题的思路逐渐清晰明朗．数学家华罗庚说过：“我解题并没有什么诀窍，只是在碰到难题时我就一退再退，直到退无可退．每每使题目由繁到简，由小到大，最后找到规律，迎刃而解．”[5]这也许是华罗庚先生对等价转化与合情推理的一种诠释吧．

2.3 培养学生的探究兴趣与成功的愉悦感是顺利实施探究教学法的动力

数学探究课与新授课、练习课、评讲课等都不尽相同，教师要及时由“台前”走向“幕后”，扮演好学生学习的指导者、帮助者、协作者的角色，努力营造和谐、平等的学习心理环境，创造多维的学习空间．教师通过积极引导学生动手操作、大胆质疑、探究发现、严谨论证，体会发现新知与探索方法的奥秘，体验运用新知解决问题的愉悦感与成就感，学生内心深处的情感体验得以被唤醒、强烈的释疑愿望得以实现，不经意间就培养了学生学习数学的浓厚兴趣．苏霍姆林斯基也曾说过：“如果你所追求的只是那种表面的、显而易见的刺激，以引起对学习和上课的兴趣，那就永远不能培养起学生对脑力劳动的真正热爱，你应该努力使学生自己去发现兴趣的源泉，让他们在这个过程中体会到自己的劳动和成就——这件事本身就是兴趣的最重要的源泉之一．”[6]

通过“寓教于乐，让学生有话可说”的教学环节，教师巧妙地为学生搭设交流对话平台，使困扰学生心中的困惑得以解决，为运用点到直线的距离公式解决问题作好铺垫；通过“曲径通幽，使学生有事可做”的教学环节，使学生认识到“点到线段距离、曲线到直线距离、点到直线的有向距离”本质都是点到点距离；学生经历一系列问题的顺利解决，了解“曼哈顿距离”衍生的来龙去脉，正是这种在学生身上发生的知识结构建构的过程，开拓了学生的心智空间，使其解决陌生问题时的恐惧感降到最低，学习数学的兴趣得到激发.解决问题的成就感与自豪感又促使学生用自己头脑中刚发现的解决问题的办法，去挑战“厚积薄发，助学生登高望远”教学环节中更加复杂抽象、意义非凡的问题．

3 结束语

布鲁纳说过：“探究是数学教学的生命线，没有探索就没有数学的发展．”探究教学法是中学数学课堂上的一种常态的教学方法，探究教学法就像调节教师的教与学生的学双边关系的一种润滑剂，激发学生主动参与学习数学的一种催化剂，激励学生致力探究新知的兴奋剂．什么时候运用探究教学法？如何运用探究教学法？探究问题如何选择？在运用探究教学法时教师的主导作用如何安排？有没有必要每节课或整节课都要用到探究教学法？等等，这些都是数学教师必须认真思考的问题．笔者认为，选择探究问题要符合课标要求，贴近学生的认知实际，摒弃“难、怪、偏”问题，确保学生探究能“探动”；其次，在探究问题时，教师要树立以生为本的教育理念，及时了解学生探究问题的困难，有针对性地培养学生的认知策略与方法，确保学生探究有“方法”；最后，教师要发挥引领、辅助、“导游”的作用，恰到好处地运用“元认知提示语”启发、暗示，不断激发学生的探究热情与兴趣，确保学生探究有“动力”．