高中生数学阅读状况的调查分析与建议

郑加金

（仙游第一中学，福建 莆田 351200）

学生的学习一般要经历“输入—内化—输出”三个阶段，对应的是“阅读—思考—表达”三个环节.高中数学的学习自然也不例外.但笔者发现，在高中数学教学实践中，数学教师往往比较重视“思考”与“表达”，不太重视“阅读”，认为“阅读”主要是语文教师要关注的任务.在学校图书馆（室），除了一些习题讲解之类的教辅材料外，与数学相关的其他书刊极为匮乏.

由于数学的符号化语言和数学本身的逻辑严谨性、高度抽象性等特点，必然使得数学阅读有别于一般的阅读，它时常要进行三种语言（文字语言、图形语言、符号语言）之间的转换，这也会给学生的数学阅读带来困难.［1］沈晓锋对160 名高二学生的测试发现，学生的数学阅读均分为50.3 分（满分80 分）.［2］陆秋汕对164 名高三学生的测试发现，学生的数学阅读均分为48.93 分（满分100 分）.［3］这些数据表明，高中生的数学阅读水平并不理想，数学阅读问题理应得到数学教师的更多关注.

高中生的数学阅读水平与其数学阅读认知、阅读习惯和方法等密切相关.为此，笔者通过问卷调查，了解高中生的数学阅读现状，并提供对策建议，以供同仁参考.

一、调查对象和方法

本次调查采取分层抽样的方法，在福建省仙游县随机抽取4 所高中发放调查问卷，共回收学生有效问卷1523 份.调查对象信息如下：高一年级726 人（47.67%），高二年级517 人（33.95%），高三年级280 人（18.38%）；城镇学生920 人（60.41%），农村学生603 人（39.59%）；男 生867 人（56.93%），女 生656 人（43.07%）.

二、调查结果分析

1.高中生认同数学阅读的重要性，但阅读兴趣不高，自主性不强

87.3%的高中生认为数学阅读对数学学习“很有用”，但是“很喜欢”和“比较喜欢”阅读数学教材的学生合计只有44.5%.新定义类题目是考查学生数学阅读能力的一类重要题型，但只有32.3%的学生喜欢这类题目，67.7%的学生并不喜欢新定义类题目，因为容易出错.

在关于学生数学阅读动机的多选题中，排在前三位的分别为“完成学分”（93.2%）、“老师的要求”（91.3%）和“为了作业与考试”（85.3%），而因为“喜欢数学阅读”“学习知识”和“学好数学”而进行阅读的学生均只有约三成.可见，大部分学生的数学阅读是出于应付考试和教师要求等外在动机，真正因为兴趣和学习内在动力而进行数学阅读的学生并不多.

问卷中设计了一道“当数学学习遇到难点时，你是否通过查阅相关的资料解决自己的问题?”来考查学生数学阅读和数学学习的自主性，选择“经常”的学生只有20.1%，选择“偶尔”“从不”的学生分别为12.3%、46.3%，还有21.3%的学生“不知道如何查阅”.可见，大部分学生的数学自主学习能力不强.

2.高中生花在数学阅读上的时间较少，阅读对象和渠道比较单一

课后除了作业外，高中生每天用于数学阅读的时间超过1 小时的占9.3%，0.5～1 小时的占11.8%，不到0.5 小时的占51.1%，还有27.8%的高中生没有开展数学阅读.在阅读对象和渠道上，72.5%的学生选择“数学教材”，12.3%的学生选择“课外教辅材料”，10.3%的学生有看“数学杂志和数学科普读物”，4.9%的学生有通过“网络”开展数学阅读.可见，学生的数学阅读以纸本阅读为主，而在纸本阅读中又以数学教材为主要对象，阅读对象和渠道比较单一.

3.高中生缺乏良好的数学阅读习惯和方法，阅读效果欠佳

有明确的数学阅读计划并严格执行的学生只有9.1%，有数学阅读计划但偶尔执行的学生占12.3%，有数学阅读计划但从不执行的学生占24%，高达55.6%的学生没有数学阅读计划.

在数学阅读过程中，习惯于在重要内容上做笔记或标记的学生占33.9%，53.6%的学生偶尔在重要内容上做笔记或标记，12.5%的学生从没试过在重要内容上做笔记或标记.关于“数学阅读过程中你是否能做到读思结合？”选择“经常”“偶尔”“没有”的学生分别为40.1%、35.6%和24.3%.“在看数学书时，你是否想过现在看的内容与以前所学内容之间的联系？”选择“经常想到”“有时想到”“从没想到”的学生分别为29.1%、52.3%和18.6%.

在数学阅读之后，习惯于对阅读内容进行概括总结的学生占25.3%，偶尔对阅读内容进行概括总结的学生占42.5%，32.2%的学生从来没有对阅读内容进行概括总结.在“数学阅读之后，你是否经常与他人讨论阅读内容？”的题项中，选择“经常”的学生占24.3%，“偶尔”的学生占33.5%，“从来没有”的学生占42.2%.

总体上看，超过半数的学生在阅读之前没有计划，四成的学生在阅读过程中能经常做到读思结合，三成左右的学生习惯于在重要内容上做笔记或标记，并将阅读内容与以前所学相联系.只有四分之一的学生在阅读后习惯于对阅读内容进行概括总结，并经常与他人讨论阅读内容.换句话说，无论是在数学阅读之前、之中、之后，大部分学生都缺乏良好的数学阅读习惯和方法，随意性强，这也导致学生的阅读效果欠佳.以数学教材阅读为例，“完全能读懂”的学生只有16.7%，63.2%的学生“大多数能读懂”，还有20.1%的学生“基本无法读懂”教材.

4.教师的阅读指导能有效提升学生的数学阅读能力，但学生获得的阅读指导并不充分

26.7%的学生认为教师的阅读指导对自己的阅读能力提升“非常有效”，39.4%的学生认为“比较有效”，二者合计66.1%；22.6%的学生认为“效果一般”，只有11.3%的学生认为“没有效果”.但在“你的数学老师是否经常指导你数学阅读的方法？”题项上，选择“经常”的学生只有23.6%，39.7%的学生选择“有时”，还有36.7%的学生认为数学教师“很少”或“从不”指导数学阅读的方法.“很想”和“比较想”获得数学阅读指导的学生分别占65.3%、26.3%，这说明大多数学生都希望获得数学阅读方法的指导，但数学教师提供的阅读指导并不充分.

三、对策与建议

1.丰富阅读材料，营造阅读氛围，培养学生的数学阅读兴趣

兴趣是最好的老师，也是维持学生学习的内在动力.但是前文的调查显示，目前高中生的数学阅读主要是迫于外在压力而不是内在动力，高中生在数学阅读的主动性、积极性和可持续性方面均存在明显的不足.有研究结果显示，高中生的数学兴趣与其对数学史、数学文化的了解程度显著相关，二者的相关系数为0.6.［4］因此，笔者建议：一是学校图书馆（室）和教室读书角可以补充增加一些数学史与数学文化、数学科普类资料，以拓宽学生的课外阅读渠道.二是数学教师可以结合教材开发一些数学史、数学趣题、数学文化等校本课程，为学生提供多样化的阅读材料.三是教师需要将数学阅读纳入课堂教学环节，将数学史与数学文化等内容有机融入课堂教学，实现课内外阅读的整合.新教材中每一章都附有“阅读与思考”“探索与发现”“文献阅读”等供学生阅读的材料，如在必修第一册第三章函数的概念与性质，教材中提供了“函数概念的发展历程”，学生阅读这些材料后，对函数仅仅肤浅了解，此时可给学生布置课外搜集有关“函数产生的社会背景”“函数概念发展的历史过程”“函数符号的故事”“数学家与函数”等深度阅读的材料.四是倡导数学“小论文”写作.如众多的数学家对函数作出了伟大的贡献，让学生选择其中的一位数学家，通过查阅书籍、上网等方式收集材料，包含图片、文字、数据以及音像材料等，整理材料，说明他们对函数发展作出的贡献，感受数学家的探索精神，形成读书报告.

此外，有条件的学校还可以通过打造数学文化角、数学研究走廊、数学学科专用教室、STEM 项目平台等，为学生的数学阅读提供环境支持.

2.加强对学生数学阅读的指导，提升学生的阅读成效

针对当前高中生缺乏良好的数学阅读习惯和方法的问题，教师亟待加强对学生数学阅读的指导和训练.具体而言，在阅读之前，教师要帮助学生制订数学阅读计划，并通过导学单引导学生关注重点问题；在阅读过程中，训练学生在重难点上做标记、读思结合、关联阅读（将所读内容与以前所学内容联系起来）、比较阅读等方法，从学科角度出发形成完整的“读数学现象—读数学本质—读数学文化”递进体系；在阅读之后，倡导学生对所读内容进行概括总结，并与同伴交流讨论.通过一段时间的指导训练，学生就会养成良好的数学阅读习惯，提升阅读成效，这反过来又会调动学生数学阅读的积极性.

案例1 北京大兴国际机场（图1）的显著特点之一是各种弯曲空间的运用.刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间弯曲性，规定：多面体顶点的曲率等于2π 与多面体在该点的面角之和的差（多面体的面的内角叫做多面体的面角，角度用弧度制），多面体上非顶点的曲率均为零，多面体的总曲率等于该多面体各顶点的曲率之和.例如：正四面体在每个顶点有3 个面角，每个面角是，所以正四面体在各顶点的曲率为2π -=π，故其总曲率为4π.

图1

（1）求四棱锥的总曲率；

（2）若多面体满足：顶点数-棱数+面数=2，证明：这类多面体的总曲率是常数.

本题考查了学生的阅读能力，特别是需要读懂“曲率”的概念，是解决问题的关键.在这类“新定义类试题”教学中，我们需要经历三个基本的过程：一是阅读新定义.提取概念或规则的关键信息，寻找已知条件，标记关键新定义名词.二是理解新定义.建立数量之间的联系，并用图形或者符号表示这个概念或者规则，明确要求什么，确定问题的方向.三是应用新定义.能够运用概念或者规则来转化问题，从而有效解决问题.

（1）如何阅读新定义？这需要找到新定义中的关键信息.通过阅读发现，在这个定义中的关键信息有三个：一是多面体的总曲率，是求解的一个非常重要的目标；二是与之相关的概念有顶点的曲率，那么顶点的距离是什么呢？提示给了一个说明，等于2π 与多面体在该点的面角之和；三是面角，什么叫面角呢？就是多面体的面的内角，叫做多面体的面角，用弧度来表示.

（2）如何理解新定义？阅读完这些概念，感觉较为抽象，那么如何加深对这个概念的理解呢？题目中提供的一个正四面体案例，其总曲率的计算过程是我们理解新定义的一个核心，为此，需要将该题中正四面体案例的文字语言转化为图形语言（如图2），发现要计算四棱锥的总曲率，只要计算四棱锥各顶点的曲率之和，写出多边形表面的所有内角即可.

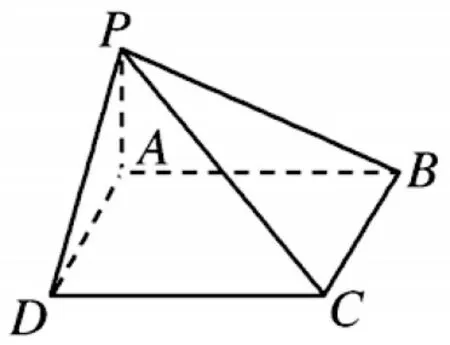
图2

（3）如何运用新定义？案例1 中的第一问可以从多面体的角度考虑，所有顶点相关的面角可以看作是所有多面体的所有多边形表面的内角的集合.如图2可得：四棱锥共有5 个顶点，5 个面，其中有4 个三角形，1 个四边形.所以四棱锥的表面内角和由4 个三角形和1 个四边形组成，则总曲率为：2π × 5-(5π +2π)=4π.第二问可以设顶点数、棱数、面数分别为nlm，设第i个面的棱数为xi，所以x1+x2+…+xm=2l，按照公式计算总曲率即可.

（4）如何浸润数学文化？本题使用的是多面体欧拉定理，即在一凸多面体中，顶点数-棱数+面数=2.其中蕴含的思想与方法，都来自课内外数学文化和数学史等知识的不断积累.所以对于这类新定义试题，第一要学会阅读课本、回归课本，理解课本对概念的过程的认识；第二要关注概念规则的形成过程，解决新定义问题就是经历阅读理解、迁移知识和运用规律的过程；第三要了解数学文化、数学史的相关内容，体会数学发展的过程，发展数学素养.

3.培养学生的语言“互译”能力，扫清数学阅读障碍

数学语言主要包括文字语言、图形语言和符号语言等.三种语言各具特点：文字语言是数学规范化、逻辑化、科学化的日常语言，图形语言生动、具体、形象，符号语言精确、简洁、抽象、概括.这三种语言之间的转换往往是学生阅读的难点，特别是符号语言与文字语言，符号语言与图形语言的“互译”，是很多学生的“短板”.

要培养学生三种语言的“互译”能力，一是教师在教学过程中可以对同一个概念或问题进行多元表征，尽可能使用多种数学语言来表述所学知识.比如：在分析平面的基本性质时，教师可以用三种语言表述其中的公理，列表（如表1）让学生在相互比较和转化中加深印象.二是可以借助几何画板、图形计算器、GeoGebra 等技术，实现符号和图形的动态联系与转换；也可以借助现实情境的创设，帮助学生理解三种数学语言.三是鼓励学生用多种数学语言进行表达交流.

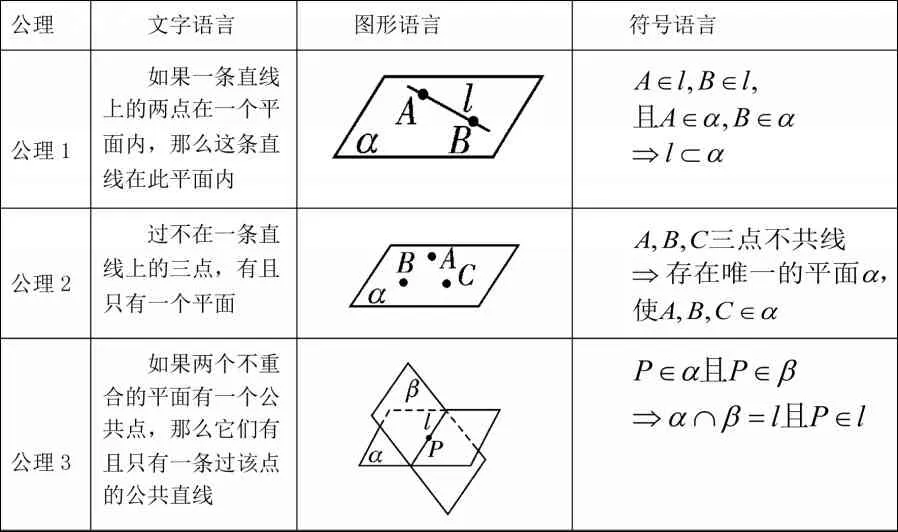
表1

总之，数学阅读能力是高中生必须具备的基本能力之一，高中生数学阅读能力薄弱问题亟待引起高中数学教师的重视.教师在实践中要注意营造数学阅读氛围，加强数学阅读指导，将数学阅读纳入课堂教学环节，“像重视语文阅读一样重视数学阅读”.