LLC谐振变流器幂指数降频启动方法
曾小波,徐恒山,薛 飞,马 鑫
(1.湖南理工职业技术学院,湘潭 411104;2.三峡大学电气与新能源学院,宜昌 443002;3.宁夏电力能源安全重点实验室(国网宁夏电力有限公司电力科学研究院),银川 750002)
由于具有软开关、无噪音和高功率密度等优点[1-3],LLC谐振变流器被工业界广泛应用[4]。在供电连续性要求严格的场合,当供电电源出现中断且需要重启时,要求LLC谐振变流器具有快速进入额定工作状态的性能,同时还要求LLC谐振变流器具有较小的启动冲击电流[5]。目前,提高LLC谐振变流器启动速度的常规做法是为其设置一个较低的启动频率,并使该频率以较大斜率逐渐降低到额定工作频率。但较低的启动初始频率会导致较高的启动输入阻抗,进而产生较大的冲击电流。文献[6]从谐振参数的角度对LLC谐振变流器的启动电流进行了优化控制;文献[5,7]从动态阻抗轨迹的角度对LLC谐振变流器的软启动进行了优化研究;文献[8]采用变占空比的方法减小了LLC谐振变流器的启动冲击电流,但占空比的变化会破坏LLC谐振变流器的软开关状态,不利于提高变流器的效率;文献[9]采用移相控制加速了LLC谐振变流器启动速度,但会在呆在启动时引入较大的冲击电流;文献[10]采用混合控制方法达到了降低冲击电流的目的,但其启动过程需要一段等待时间,降低了开机效率。可以看出,采用传统方法难以同时解决LLC谐振变流器启动速度慢和启动冲击电流大的问题。在此背景下,本文提出了幂指数降频启动方法,将LLC谐振变流器的启动频率设置为较大值,并在启动后幂指数降频,使阻抗快速降低并达到额定值,在实现快速启动的同时还可降低LLC谐振变流器的启动冲击电流。
1 LLC谐振变流器
图1为LLC谐振变流器电路原理[11-13]。图1中,Uin和Uo分别是输入电压和输出电压,Q1~Q4和D1~D4分别是原边高频开关器件和副边整流二极管,Cr、Lr和Lm分别是谐振电容、谐振电感和励磁电感,T为变比为n∶1的变压器,Co和Rload分别是输出侧滤波电容和等效负载电阻,iin和io分别是输入电流和输出电流,iQ和iD分别为流过原边开关器件和副边整流二极管的电流,ir、im和is分别是谐振电流、励磁电流和变压器副边绕组的电流,iC和iload分别是流过Co和Rdc的电流。
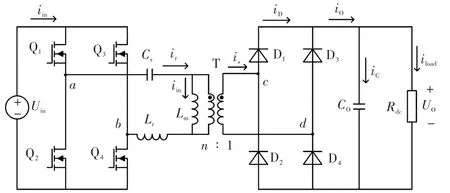
图1 LLC谐振变流器的原理Fig.1 Schematic of LLC resonant converter
LLC谐振变流器常用的控制方式有脉冲频率调制PFM(pulse frequency modulation)[6]、脉冲宽度调制PWM(pulse width modulation)[14-16]及PWM+PFM控制[17-18]。PWM控制必须要解决开关器件的电压振荡问题,PWM+PFM控制会增加控制芯片的计算内存和计算难度。相比于PWM+PFM控制,PFM控制较易实现且控制器成本较低;相比于PWM控制,PFM控制的原、副边器件均能实现软开关,容易解决器件的电压振荡问题。因此,PFM控制在LLC谐振变流器中应用较为广泛。当LLC谐振变流器采用PFM控制时,可用基波近似等效FHA(fundamen⁃tal harmonic approximation)法进行交流等效分析[19-20]。
LLC谐振变流器的交流等效电路如图2所示。在图2中,uab、ucd分别为原、副边高频方波电压的基波分量,Rac,s为直流负载电阻Rload等效到ucd处的交流等效电阻,ucd,p和Rac,s分别为归算到变压器原边的基波分量和交流等效电阻。
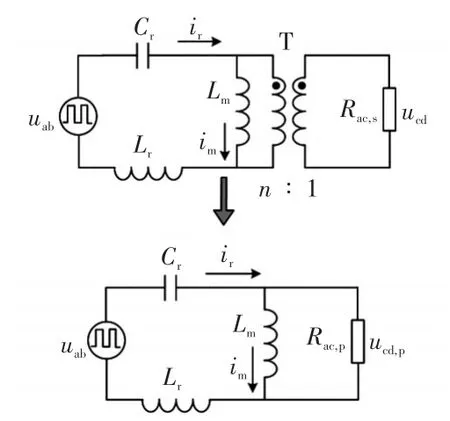
图2 LLC谐振变流器的交流等效电路Fig.2 AC equivalent circuit of LLC resonant converter
2 启动特性分析
LLC谐振变流器的等效输入阻抗[21]为
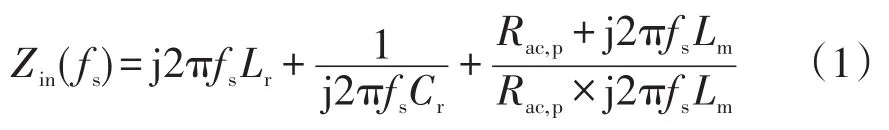
在启动瞬间,输出电压为0 V。二极管对ucd起到箝位作用,为了方便分析启动电流,可以近似认为ucd,p=ucd,s=0 V,则启动瞬间的输入阻抗Zin,start可以近似表示为

启动冲击电流Istart,pk为
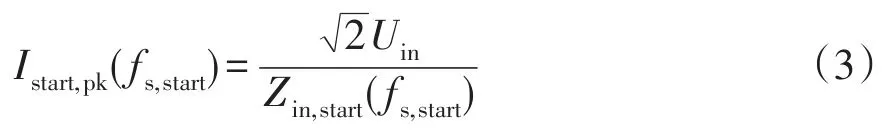
LLC谐振变流器的启动控制原理如图3所示,图中:uo为输出电压的实时值;Uo,ref为ucd的参考值;fs,act为电压环的输出频率;fs,start为电压环启动频率,可根据启动情况进行设置;fs为LLC谐振变流器的实际开关频率;S1~S4为开关器件Q1~Q4的触发信号。
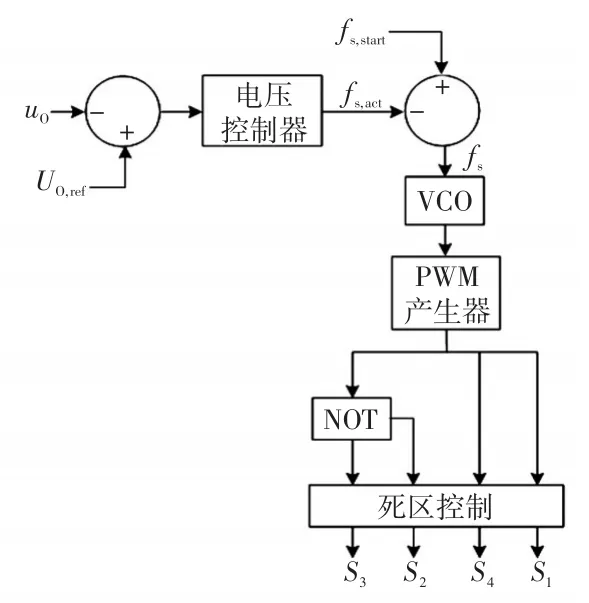
图3 LLC谐振变流器启动控制原理Fig.3 Schematic of start-up control for LLC resonant converter
LLC谐振变流器的实际开关频率 fs可表示为
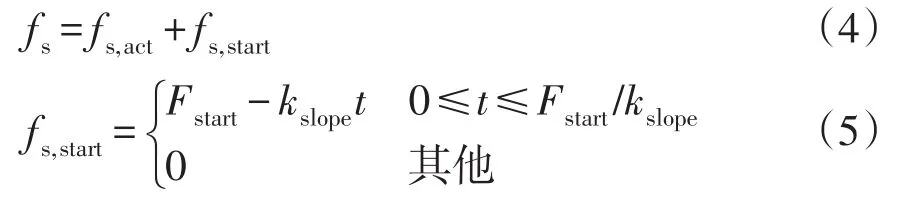
式中:Fstart为设置的启动频率;kslope为 fs,start的下降斜率。将式(4)和式(5)代入到式(2)和式(3)中,可求得LLC谐振变流器的输入阻抗和启动冲击电流。这种情况下,得到的是传统线性降频启动法的阻抗特性和冲击电流特性,虽然将 fs,start设置为较大值,可以达到增加启动输入阻抗、减小启动电流的目的,但在kslope给定的情况下,需要较长的启动时间来完成LLC谐振变流器的启动过程,即采用传统线性降频启动方法会导致较长的启动时间。为了增加启动瞬间的输入阻抗,降低启动冲击电流,本文提出了一种幂指数启动法。本方法将启动频率 fs,start替换为

启动过程完成后,LLC谐振变流器以额定工况运行,此时LLC谐振变流器的工作频率为额定开关频率 fnormal,输入阻抗为额定输入阻抗Zin,normal,表示为
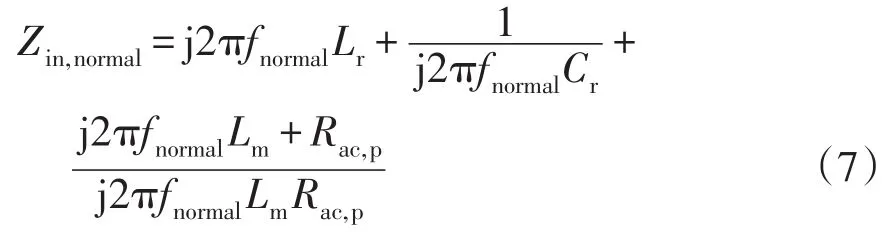
图4展示了传统线性降频启动法和本文所提幂指数降频启动法的 fs,start与时间t之间的关系曲线,其中,Tstart为启动时间。各方法中:Po=2 kW,Uo=400 V,NT=1,Lr=41 μH,Lm=160 μH,Cr=72 nF 。由图4可见,在传统线性降频启动方法中,虽然kslope=5.8×106,远大于幂指数启动方法中kslope=112,但其启动时间约为70 ms;当采用幂指数降频启动法时,LLC谐振变流器的启动时间约为15 ms,这证明幂指数降频启动方法相比于传统线性降频启动方法可更快地完成LLC谐振变流器的启动过程。

图4 fs与t的曲线关系Fig.4 Curve of relationship betweenfsandt
幂指数降频启动法采用较小的kslope值(112)即可实现快速启动,而传统线性降频启动法即使采用较大的kslope值(5.8×106)也达不到幂指数降频启动法的启动速度。
图5为LLC谐振变流器的输入阻抗Zin与启动后时间t的关系曲线,方法中,Po=2 kW,Uo=400 V,NT=1,Lr=41 μH,Lm=160 μH,Cr=72 nF。由图5可见,采用传统线性降频启动法时,启动瞬间的输入阻抗约为150 Ω,随着时间的推移,输入阻抗从Zin,start=150 Ω逐渐降低到额定输入阻抗Zin,normal=52.5 Ω,该过程耗时约为70 ms;采用幂指数降频启动法时,启动瞬间的输入阻抗也是150 Ω,随着时间的推移,输入阻抗从150 Ω降低到额定输入阻抗Zin,normal=52.5 Ω,该过程耗时约为15 ms,这说明幂指数降频启动法可有效缩短LLC谐振变流器的启动时间,提高LLC谐振变流器的启动速度。

图5 Zin与t的曲线关系Fig.5 Curve of relationship betweenZinandt
图6展示了传统线性降频启动法和本文所提幂指数降频启动法所得到的电流峰值Iin,pk与时间t之间的变化曲线,方法中,Po=2 kW,Uo=400 V,NT=1,Lr=41 μH,Lm=160 μH,Cr=72 nF。
经济学中“杠杆”和“杠杆率”最早出现在微观经济学领域,其定义是单个企业借入资本相对于自有权益资本的比率,用来衡量该企业的负债经营程度[3]。负债经营可以降低企业税负,因而现代企业都采取负债经营的方式。由于负债率越高减税效果越好,所以有理论认为企业的最优负债率为100%,但是负债需要承担债务成本,负债率过高会增加企业成本,甚至会引发债务危机,因而企业的负债率应当保持在50%以上100%以下[4]。
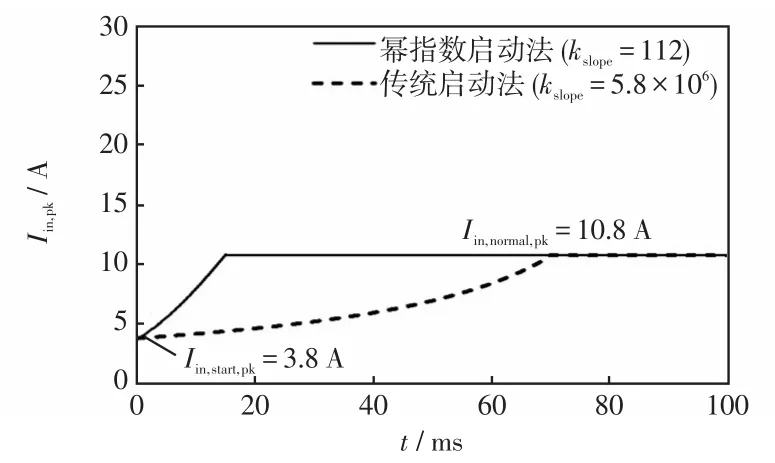
图6 Iin,pk与t的曲线关系Fig.6 Curve of relationship betweenIin,pkandt
在启动瞬间,2种启动方法的输入电流峰值Iin,start,pk几乎相等,约为3.8 A;但在t=0 s以后,幂指数降频启动法以更快地速度接近额定峰值电流Iin,start,pk=10.8 A。
3 实验验证
图7为传统线性降频启动法得到的启动电流的理论计算结果和仿真结果,从图中可以看出,理论结果非常接近仿真结果。

图7 采用传统启动法得到的启动电流结果Fig.7 Results of start-up current obtained using the traditional start-up method
在启动过程中,仿真结果与理论计算结果之间存在较小误差,这是因为本文的理论分析是基于FHA得到的,而FHA法仅在谐振点处才能得到无差结果,而LLC谐振变流器在启动过程中的开关频率是逐渐从500.00 kHz降低到谐振频率91.17 kHz,在此过程中,开关频率偏离谐振点的距离较远,导致了理论结果与仿真结果之间存在一定误差,而这种误差在窄开关频率范围内较小,不会对开关器件的正常运行和变流器的正常工作带来较大影响,基本可忽略不计。
图8展示了幂指数降频启动法在启动过程中的启动电流理论计算结果和仿真结果,可见,理论结果与仿真结果之间误差较小,这种误差也是源于FHA法,较小的误差不会影响幂指数降频启动法分析LLC谐振变流器启动特性的结果。

图8 采用幂指数启动法得到的启动电流结果Fig.8 Results of start-up current obtained using the power exponent start-up method
对比图8与图7的结果可以发现,从t=0 ms开始,图8中采用幂指数启动法的启动电流以更快的速度上升到额定工作状态。这说明,相比于传统线性降频启动法,所提幂指数降频启动法可以加速LLC谐振变流器的启动过程。
图9为开发的LLC谐振变流器样机,样机参数如表1所示。为了减小LLC谐振变流器样机的体积,采用变压器的漏感充当谐振电感,将谐振电感集成在变压器中。图10和图11分别展示了采用传统线性降频启动法和幂指数降频启动法得到的LLC谐振变流器的实测谐振电流波形。

图9 LLC谐振变流器样机Fig.9 Prototype of LLC resonant converter

表1 LLC谐振变流器的样机参数Tab.1 Parameters of LLC resonant converter prototype
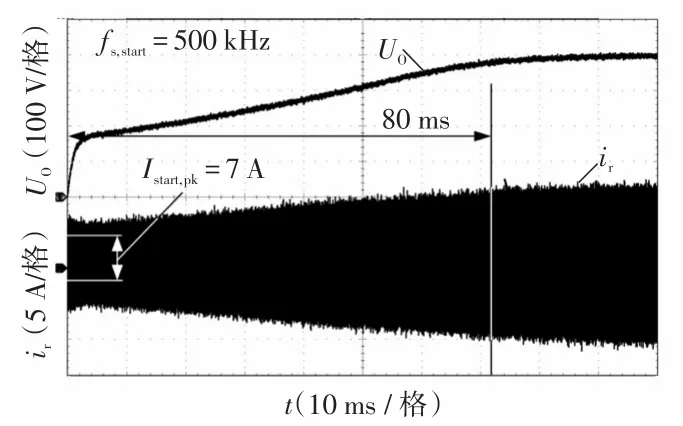
图10 当 fs,start=500 kHz时传统线性降频启动法得到的UO和ir的实测波形Fig.10 Measured waveforms ofUOandirobtained using the traditional linear reducing frequency startup method whenfs,start=500 kHz
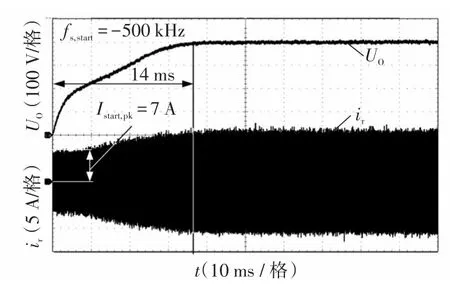
图11 当 fs,start=500 kHz时幂指数降频启动法得到的UO和ir的实测波形Fig.11 Measured waveforms ofUOandirobtained using the power exponent reducing frequency strat-up method whenfs,start=500 kHz
从图10中可以看出,采用传统线性降频启动法时,LLC谐振变流器从开机到额定电压(满载情况下,输出电压达到400 V)的过程耗费的时间约为80 ms;在t=0 s,谐振电流ir的峰值约为7 A;输出电压达到稳定时,谐振电流峰值约为11 A,与理论计算值10.77 A之间存在较小误差,该误差可能来源于测量仪器。
从图11中可以看出,在启动时刻,幂指数降频启动法的谐振电流峰值基本与传统线性降频启动法得到的结果相同,但幂指数降频启动法会使谐振电流峰值以更快的速度达到稳态,启动时间更短,约14 ms。由于幂指数降频启动法在较小的kslope值时即可实现快速启动,因此,可进一步提高幂指数降频启动法的初始启动频率以降低启动冲击电流。
图12展示了当 fs,start=700 kHz时,幂指数降频启动法得到的实测波形,此时,启动时间比图11中的启动时间较长,但依然比图10中传统线性降频启动法的启动速度更快,且冲击电流相比于图10和图11中的更小。也就是说,相比于传统线性降频启动法,在不影响启动速度的前提下,幂指数降频启动法可将 fs,start设置得更大,以降低启动冲击电流。

图12 当 fs,start=700 kHz时幂指数降频启动方法得到的Uo和ir的实测波形Fig.12 Measured waveforms ofUoandirobtained using the power exponent reducing frequency start-up method when fs,start=700 kHz
表2对传统线性降频启动法和幂指数降频法的实验结果进行了对比,可以发现,当 fs,start均设置为500 kHz时,2种启动方法得到的Istart,pk相等,但此时幂指数降频启动法的启动速度更快。
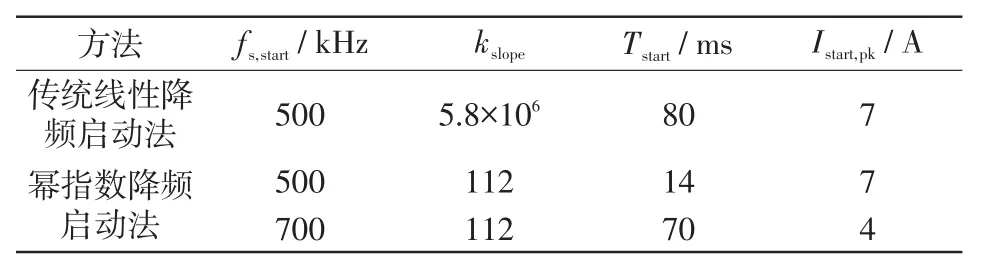
表2 两种启动法的对比Tab.2 Comparison between two kinds of start-up method
从表2中可以看出,提高幂指数降频启动法中的 fs,start值,可达到降低Istart,pk的目的,但会增加启动时间;通过合理设置kslope和 fs,start,能够保证幂指数降频启动法的Istart,pk低于传统线性降频启动法的Istart,pk,同时,还能保证幂指数降频启动法的Tstart小于传统线性降频启动法的Istart,pk,也就是说,通过设置合理的 fs,start和kslope,可使幂指数降频启动法比传统线性降频启动法具有更小的启动冲击电流和更快地启动速度。
4 结语
从阻抗特性对LLC谐振变流器的启动冲击电流和启动速度进行了分析,将幂指数降频启动法引入到LLC谐振变流器的启动控制中,采用理论分析、仿真分析和实验法对幂指数降频启动法进行了验证。实验结果证实了幂指数降频启动法在降低LLC谐振变流器的启动冲击电流的同时还能有效地提高满载状态下的启动速度。

