一类度互质的无标度网络研究

苏志忠+刘焕龙+孔祥泉

摘 要： 本文提出了一类度互质的严格无标度网络模型，刻画出其节点分布规律，并基于这种模型进一步分析了幂指数大于2与小于等于2时无标度网络拓扑性质的区别。

关键词： 幂指数 无标度网络 平均度

一、引言

20世纪末以来，复杂网络的研究逐步渗透到物理、生命科学、社会科学等众多不同的领域，成为网络时代科学研究极其重要的挑战性课题。这股研究热潮的起源是由国际上两项开创性工作掀起的，其一是1998年Watts和Strogatz在Nature杂志上发表的论文，该文引入了小世界（Small-World）网络模型，描述了完全规则网络及完全随机网络之间的异同与完全规则网络到完全随机网络的转变。具有小世界性质的网络既具有与规则网络相似的聚类特性，又具有与随机网络相似的较小的平均路径长度。第二项重要工作是1999年Barabási和Albert在Science上发表的论文，该文基于对WWW的实证研究，指出众多实际存在的复杂网络的节点度分布具有幂律规律而不是均匀分布或高斯分布。由于幂律分布没有明显的特征长度，在概率论中具有无标度特征性质的分布仅有幂律分布，该类网络又被人们称为无标度（Scale-Free）网络[2]。由于现实世界中大多数无标度网络的标度指数介于2和3之间，之后的几年人们只对幂指数大于2的无标度网络进行了研究，直到2005年，Seyed-allaei等关注到幂指数小于2的网络，他们基于随机不相关的无标度网络研究了网络的平均度、结构最大度及聚集系数，指出了幂指数小于2和幂指数大于2的无标度网络的拓扑性质明显不同。接下来国内学者吴俊、王林、刘艳霞等进一步研究了幂指数不大于2的无标度网络的拓扑性质。基于前人的工作，受刘艳霞提出的一种素数网络模型的启发，笔者观察到这种严格的无标度网络模型具有以下局限性：（1）只能为素数。（2）幂指数只能为整数。

因为只有幂指数为整数时才能保证度及其相应的节点数都为整数。为了更好地研究无标度网络的拓扑性质，本文提出了一类度互质的无标度网络模型，这种严格的无标度网络模型中的度之间只需满足互质条件，且幂指数的数值可以取任意有意义的有理数。

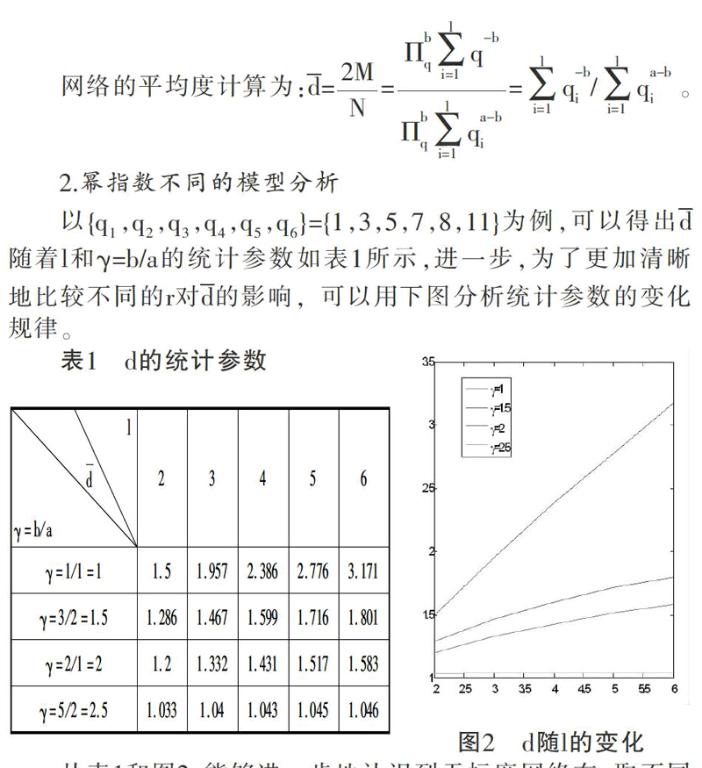
从表1和图2，能够进一步地认识到无标度网络在γ取不同值时，呈现出截然不同的性质。当γ>2时，网络平均度随着网络规模的增大基本不变，边数缓慢增加，网络相对比较稀疏。而当1≤γ≤2时，网络平均度随着网络规模的增大呈迅速上涨趋势，也就是说，最小度节点所占的比例越来越小，最大度节点或者度数较大的节点所占的比例增大，网络的边数相对于节点快速增大，网络越来越稠密。

四、结语

基于前人的结果，本文提出了一类度互质的无标度网络模型，通过研究它的度分布特征，进一步验证了幂指数大于2和幂指数不大于2的无标度网络的拓扑性质，对进一步研究无标度网络的拓扑性质具有一定的作用。下一步，我们力争找到这类网络的实际应用，并基于这种网络模型进一步研究幂指数在不同范围时拓扑性质及路由算法。

参考文献：

[1]Watts D J，Strogatz S H.Collective dynamics of small-world networks[J].Nature.1998，393（6684）：440-442.

[2]Albert R，Jeong H，Barabási A.Internet：Diameter of the world-wide web[J].Nature.1999，401（6749）：130-131.

[3]Barabási A，Albert R.Emergence of scaling in random networks[J].Science.1999，286（5439）：509-512.

[4]Seyed-Allaei H，Bianconi G，Marsili M.Scale-free networks with an exponent less than two[J].Physical Review E.2006，73（4）：46113.

[5]吴俊等.标度指数不大于2的无标度网络的若干性质[J].系统科学与数学，2008，7：6.

[6]王林等.复杂网络的度分布研究[J].西北工业大学学报，2006，24（4）：05-409.

[7]王林等.关于无标度网络中Hub节点的研究[J].计算机应用，2010，11：63.

[8]刘艳霞.基于代数图论的复杂网络的拓扑性质和构造方法研究[D].华南理工大学.