厚度幂指数分布管状结构耐撞性设计准则与方法研究*
徐峰祥,张 锁,武昆迎
(1. 武汉理工大学现代汽车零部件技术湖北省重点实验室,湖北 武汉 430070;2. 武汉理工大学汽车零部件技术湖北省协同创新中心,湖北 武汉 430070)
连续变截面或者变厚度板技术是一种新兴的薄板轧制工艺[1-3],在满足车身结构性能的基本前提下通过该技术可以使车身零部件进一步减轻重量。由于变厚度技术减少了复杂的焊接工序,所以具有一定成本优势,为进一步推广应用提供了良好的基础,研究变厚度板技术对车身轻量化具有较大作用[4]。
与拼焊板结构相比,变厚度板结构的特点是厚度属性可以灵活变化,再加上厚度的连续特性,使其不会出现强度或者应力突变等缺陷;其次,变厚度板技术也不会遇到拼焊板所固有的焊接难题。变厚度板技术的基本原理是通过辊轧轮的上、下运动轧制而形成具有一定厚度分布的板材[5-7],这样采用较少重量的材料就可以制成车身结构件,促使其在汽车车身零部件结构中具有一定的应用前景[8]。
Kopp等[9-10]最早从成形角度研究变厚度板轧制控制以及回弹等问题中发现用较少的材料就可以加工成比较高刚度和强度的车身零部件。包向军[11]从试验角度和数值模拟方面研究了变厚度板的弯曲和回弹;任灏宇等[12]在控制模型及理论基础等方面对连续变厚度板进行了研究;姜银方等[13]通过有限元模拟研究了变厚度板塑性变形过程。
但上述研究重点基本都是围绕其成形工艺特性,仅有少数学者在轻量化和耐撞性等方面进行了研究。从Yang等[14-15]的研究可以得出结论,变厚度结构具有较高的材料利用率和较大的设计灵活性;兰凤崇等[16]引入充分利用材料特性的连续变厚度板,实现前纵梁的耐撞性和轻量化双重目标,设计结果表明,变厚度结构的变形量和加速度峰值较小,质量也有一定的降低,降幅达到5.21%,并且并没有明显削弱耐撞特性。然而,少量的研究不足以对变厚度结构进行合理的设计。
本文中,研究厚度连续分布的管状结构的耐撞性设计准则及方法,假定厚度的梯度变化形式是幂指数分布,推导等质量条件下其与其它管状结构(比如均匀管、拼焊管以及锥管等)之间的定量解析关系并对比其吸能特性,并对幂指数梯度变化形式的管状结构进行耐撞性优化设计。
1 厚度连续分布形式及数值模型
1.1 厚度分布假设
理论上本文封闭的管状结构应该是通过板结构的折弯、激光焊接等工艺制造而成,由于焊缝较窄,对试件性能的影响较小,尤其是对动态大变形耐撞性问题,焊缝带来的影响更小,所以在数值模拟中可以将焊缝视为共节点连接方式,即不考虑焊缝的材料和尺寸属性。图1是厚度连续递增的薄壁结构轴向碰撞示意图,上端部壁厚ttop和下端部厚度tbot分别是碰撞开始端和末端,中间过渡厚度由某种特定函数关系给定。
从管状结构的轴向压溃过程可知,薄壁结构的碰撞端即开始端首先发生压溃变形,所以管状吸能结构的厚度分布应该是从最薄逐渐过渡到最厚,即碰撞端的厚度应该是最薄的(ttop=tmin),固定端则最厚(tbot=tmax),这样就可以使管状结构更容易发生渐进式(或手风琴式)折叠。与文献[17]中功能梯度泡沫材料的密度分布形式相类似,本文将特定管状结构的厚度假设为幂指数分布形式,也就是厚度沿着轴向逐渐增大的形式(图2),最小和最大厚度分别用t0和tm表示,即:
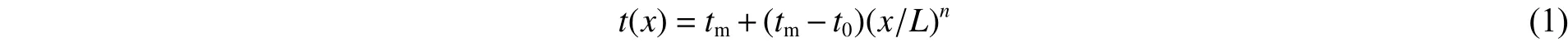
式中:n为梯度指数,x为距离管状结构上端部的长度,L为薄壁管的总长度。

图1 厚度连续递增的薄壁结构轴向碰撞示意图Fig. 1 Schematic of thin-walled structures with thickness increasing under axial crashing

图2 厚度比沿着长度方向的变化情况Fig. 2 Thickness changes of thin-walled structures along the length direction
1.2 数值模型及验证
为了方便讨论问题,考虑到目前制造工艺方面的不足,此处通过简单的线切割手段得到厚度线性分布(n=1.0)的圆管结构(图3)。碰撞端(上端)有最小的厚度值tmin,固定端(下端)有最大的厚度值tmax。本文试件的尺寸为:t0=tmin=1.2 mm,tm=tmax=1.5 mm,D=45 mm,L=120 mm。所采用的材料为铝合金(AA6061-T5),弹性模量为68.2 GPa,密度为2 700 kg/m3,泊松比为0.33,材料属性通过准静态拉伸试验(2 mm/min)测得,得到的应力应变曲线如图4所示。
如果将变厚度管分割成若干层,那么均匀管的等效厚度(与幂指数分布管有相同质量)为:

式中:ti为第i层的厚度,NS为总层数,Le为单层长度。通过不同层数构造的收敛性分析,此处设定31层已满足要求。
如图5所示,数值模拟和试验得到的峰值碰撞力分别为31.5和30.1 kN,相对误差控制在5%以内;另外,从变形模型和褶皱数量来看,结果同样具有良好的吻合程度,这证明了该模型可以进一步预测其他幂指数分布管的变形模式和行为。

图3 幂指数管状结构示意图Fig. 3 Schematic showing thickness grading patterns in the axial direction
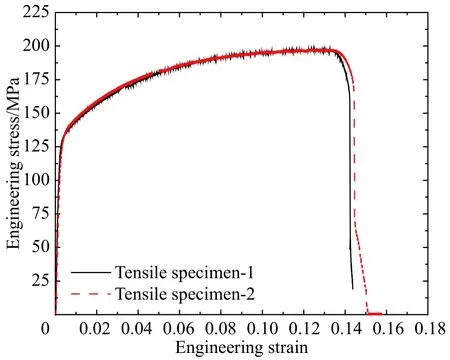
图4 材料应力应变曲线Fig. 4 Stress-strain curve of material
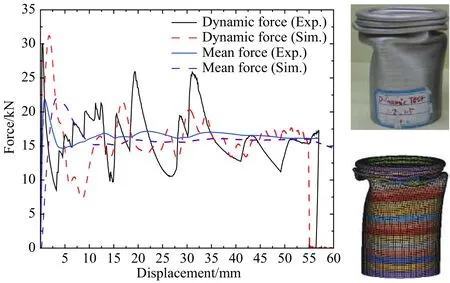
图5 幂指数分布管(FGT)的试验测试和数值结果比较Fig. 5 Comparisons of experimental and numerical results for tubes
2 参数解析关系及设计准则
均匀等直管和锥管结构(图6)都是常见的薄壁吸能结构。决定锥管碰撞性能的参数是壁厚和锥角;而决定变厚度管耐撞性的是梯度函数。采用等质量原则进行参数的等效处理,得到不同管状结构几何参数之间的关系,这样可以方便改变结构参数,分析在等质量条件下不同截面形状的碰撞特性。
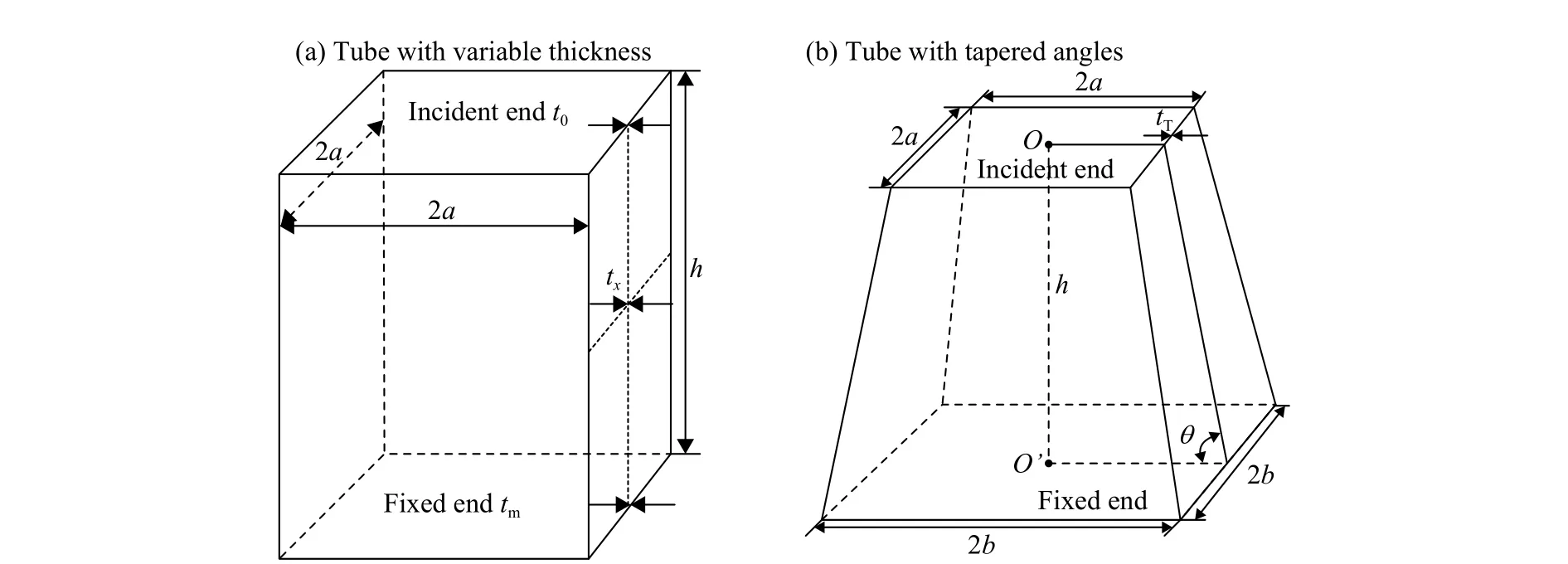
图6 变厚度管和锥管的示意图Fig. 6 Schematics of variable thickness and tapered tubes
2.1 幂指数分布管与均质等直管之间的等效关系
在相同体积或者质量的情况下,等直管和幂指数分布管的几何参数之间的关系可以写成:

式中:h是管状结构的高度,tU是等直管的等效厚度。
等直管的等效厚度tU和幂指数分布管的指数n能够显示表达为

由式(4)可知,对于特定的厚度分布,等直管具有相对应的等效厚度。
2.2 幂指数分布管与锥管之间的等效关系
与前面相似,幂指数分布管和锥管相关的几何参数之间的关系可以表达为:

式中:tT和θ分别为锥管的厚度和倾斜角度,a为方管宽度的一半或圆管的半径。
如果锥管的厚度tT等于幂指数管的最小厚度t0,那么决定性能的梯度指数n和倾斜角度θ之间存在一定的关系:

所以存在有特定倾斜角度θ的锥管,即:
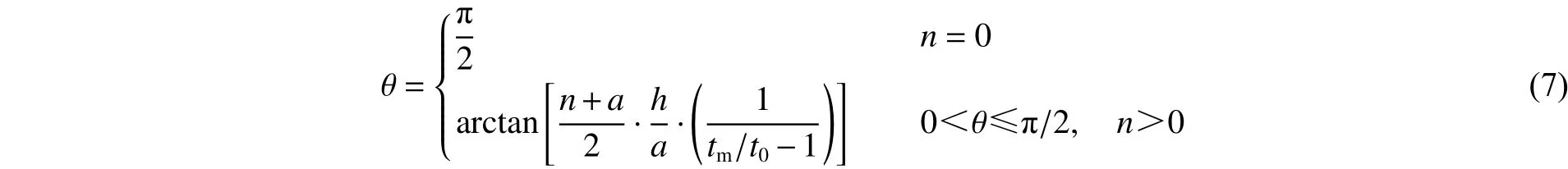
更进一步地,n>0时,有:

式中:C0=h/[2a(tm/t0-1)]。
若锥管壁厚tT与幂指数分布管的下端厚度tm相同,那么将存在以下关系:

式中:C0=h/[2a(t0/tm-1)]。
注意到上述解析关系对截面是方形和圆形的管状结构都是一样的,为了讨论方便,在此仅对方形截面的管状结构进行研究。
2.3 幂指数分布管的设计准则
在实际的工程应用中,锥管的倾斜角度不应过大(假设该角度不小于π/3),因此:

根据式(10),有:

即:
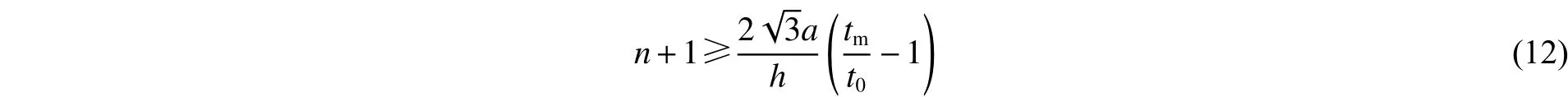
对于tT=tm的情况,锥管上端尺寸大于下端,即倾斜角度为钝角(θ>π/2),这就要求2a>2h tan (θπ/2),则有:
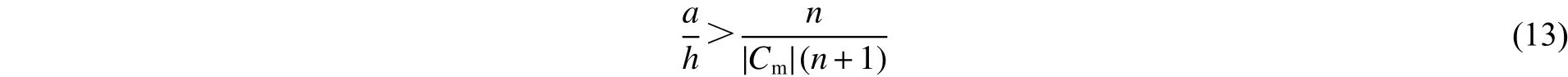
将Cm代入至式(13)可以得到幂指数分布管的几何参数与梯度指数之间的表达式:
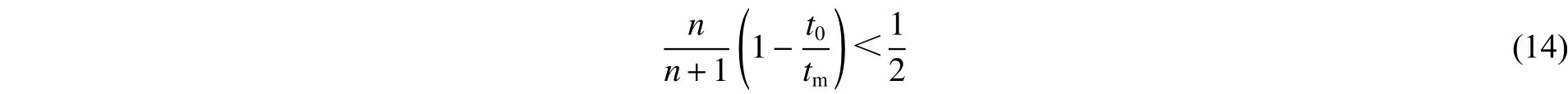
3 耐撞性分析
首先对比幂指数分布管(FGT)、拼焊管(TWB)、均匀管(UT)之间的吸能特性,有限元模型如图7所示。幂指数分布管的上、下端厚度分别为0.8 mm和2.2 mm;采用厚度不同、材料相同的两拼组合,其厚度分别为幂指数分布管的上/下半部分的等效厚度,均匀管等效厚度由式(2)给出。不同指数n下等效拼焊管及均匀管的厚度见表1。
从图8(a)可以看出,当n<1.0时,拼焊管的峰值载荷位于均匀管和幂指数管之间,幂指数分布管所得到的峰值载荷最小,这说明其有效降低了峰值碰撞力,具有明显的安全优势。而均匀管的峰值碰撞力在不同的梯度指数下均是最大的。另外,幂指数分布管在比吸能指标上也具有明显的优势(图8(b))。综上所述,幂指数管是一种理想的吸能薄壁结构。

图7 三种管结构的有限元模型Fig. 7 Finite element model of three tubular structures
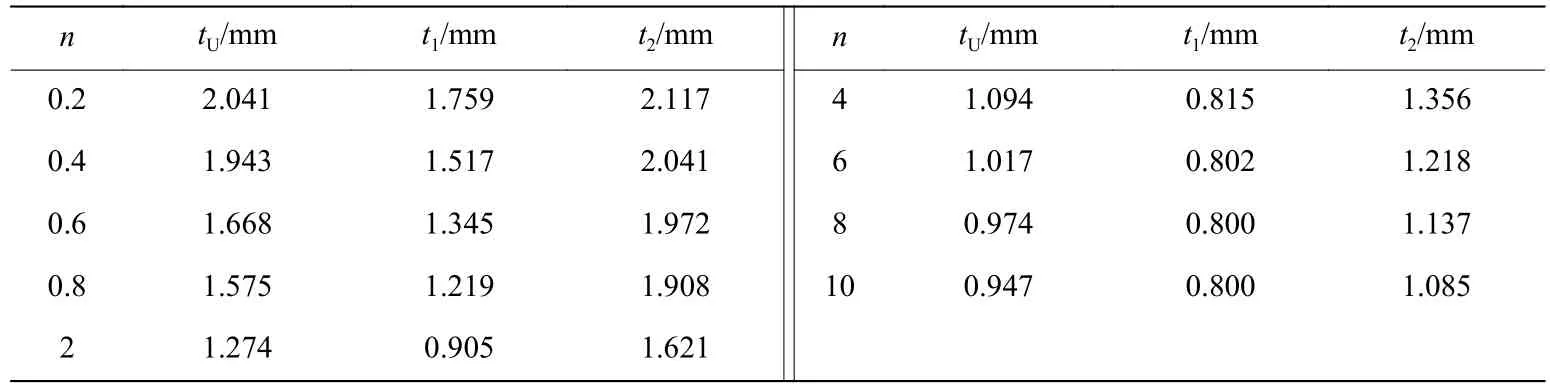
表1 三种管状结构在相同质量下的厚度分布Table 1 Thickness distributions of three tubes with the same weight

图8 三种管状结构的吸能特性对比Fig. 8 Comparisons of energy absorption capacity of three kinds of tubes
图9是幂指数管与锥管在不同情况下的碰撞性能对比,A、B分别代表0<n≤1和1<n≤10,1~6代表不同的锥管厚度,从1变化到6,锥管厚度不断增大,角度也逐步倾斜。可以看出幂指数管的碰撞载荷随着梯度值的不断增大而减小。

图9 幂指数分布管和锥管在不同情况下的碰撞性能对比Fig. 9 Crashing performance of tubular structures with power exponent and tapered angles
综上所述,幂指数分布管的比吸能和峰值碰撞载荷等碰撞指标优于等直管和锥管,主要的原因在于幂指数管的厚度是按照一定梯度形式变化的,可使幂指数管的耐撞性效果能够进行合理预测和评估,使得压溃变形程度更平缓并可控。
4 设计过程与讨论
对于不同的梯度指数,幂指数分布管的厚度分布是不同的,所以在此将梯度指数作为设计变量,并将比吸能和峰值碰撞力设定为耐撞性指标,这样幂指数分布管状结构的多目标设计问题就可以表达函数:
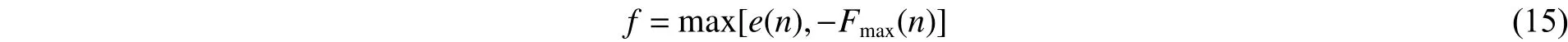
幂指数管状结构的碰撞过程是非线性行为,在数学上不可能获取目标函数的解析函数,所以通过近似模型技术(如响应面等)来拟合耐撞性响应[18]。需在两个设计空间0≤n≤1和1≤n<10内随机选取测试点来构建SEA和Fmax的响应面模型。反求出响应面近似模型的参数之后,接下来需检验模型的精度。常用的误差估计方式有决定系数R2,相对平均绝对误差 δavg,相对最大绝对误差δmax:

式中:yi、和分别为响应的实测值、预测值和预测值的平均值。表2和表3是比吸能响应面近似模型的精度评估结果,其中上标G和U分别表示幂指数分布管和均匀管,可以看出阶数越高,模型精度越高。
图10给出了通过响应面模型得到的幂指数分布管和均匀管的优化结果(Pareto前沿),幂指数分布管的Pareto前沿位于右上方,这表明其比均匀管具有更好的优势。通过不同阶数响应面模型得到的均匀管的设计结果基本一致,而对于幂指数分布管的Pareto前沿解来说具有不同的结果。比如,在图10(a)中点A的左边,具有更高的吸能能力(拥有阶数更高的响应面),在点B的右侧,通过二阶多项式近似模型可以得到更好的优化结果,说明较高精度的响应面近似模型并不一定可以得到更优的结果。
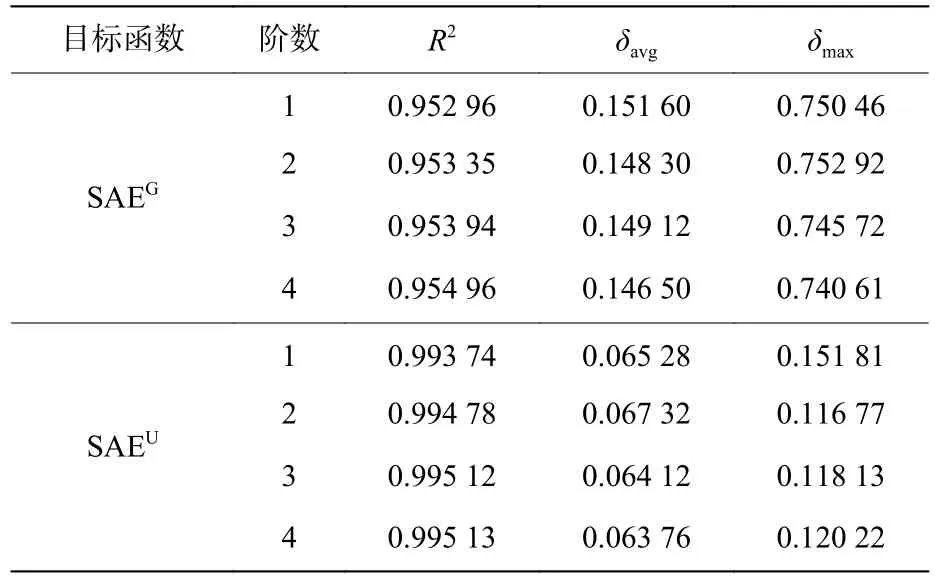
表2 比吸能响应面近似模型的精度评估(0≤n≤1)Table 2 Accuracy estimate of response surface model of SAE (0≤n≤1)

表3 比吸能响应面近似模型的精度评估(1<n≤10)Table 3 Accuracy estimate of response surface model of SAE (1<n≤10)
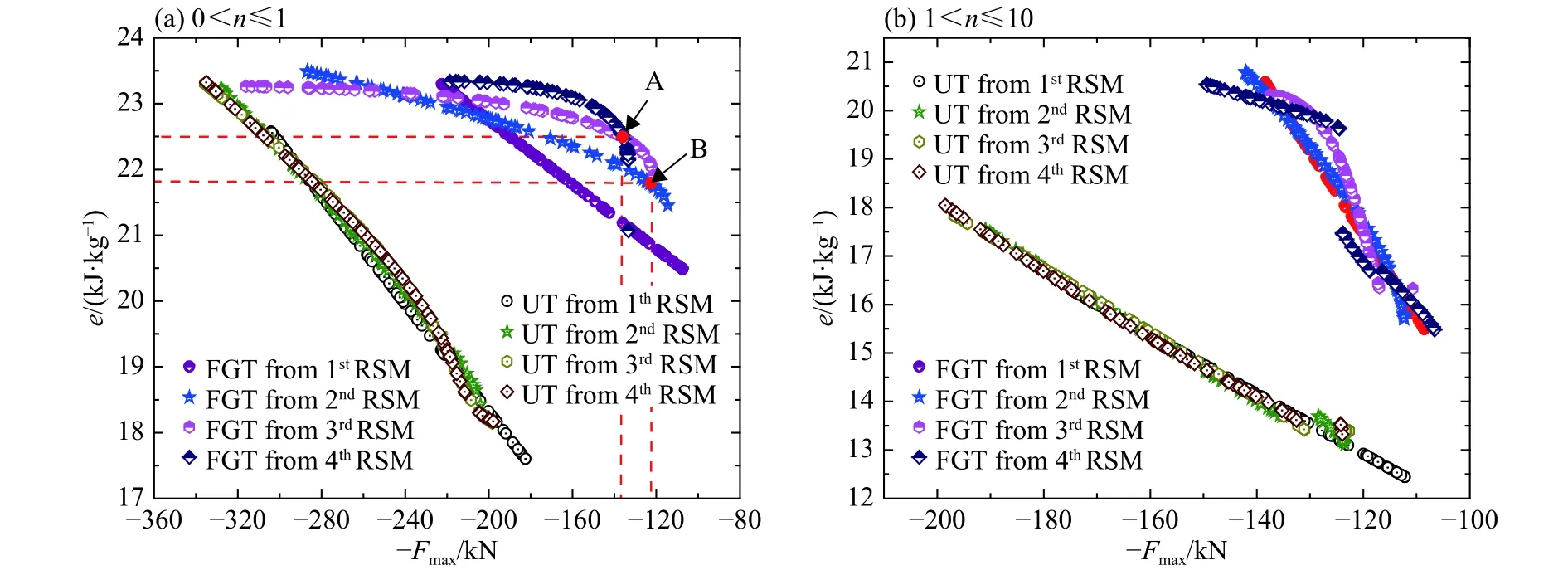
图10 不同响应面模型(RSM)的幂指数分布管(FGT)和均匀管(UT)的Pareto前沿解Fig. 10 Pareto solutions of tubular structures with power exponent (FGT) and uniform thickness (UT) by different response surface models (RSMs)
5 结 论
本文研究了一种厚度幂指数分布管状薄壁吸能结构,分析了不同厚度梯度对其耐撞性能的影响,最后研究了其耐撞性优化设计问题,主要得到以下结论:
(1) 根据质量等效原则,推导出了三种吸能结构(幂指数管、等直管和锥管等薄壁结构)的尺寸参数之间的关系,为对比分析其耐撞性能提供了良好的数据基础;
(2) 得到了幂指数分布管的几何设计准则,即梯度指数应满足不等式条件n+1≥a/h(tm/t0-1);
(3) 将梯度指数作为优化设计变量,在两个设计区间内采样并分别构建合理的响应面近似模型,通过对比证实高阶响应面近似模型得到的设计结果不一定是最优的。

