火箭发动机燃烧过程的鲁棒非脆弱H∞控制*
吴玉彬,张合新,朱开锐,李国梁,惠俊军
(1. 火箭军工程大学控制工程系,陕西 西安 710025;2. 中国人民解放军陆军重庆军代局,重庆 400060;3. 中国人民解放军96037部队,陕西 宝鸡 721013)
时滞现象常存在于导弹的制导、飞行器的控制与航天系统当中,例如某液体火箭发动机燃烧室内的燃烧过程就包含了非常明显的时滞,其动态模型可简化为一个不稳定的时滞系统[1-2]。在系统的分析与控制器的设计中,如果忽略时滞的影响,往往导致系统不稳定以及性能的下降。因而近年来,时滞系统的稳定性分析及控制问题成为一个热点的研究领域[3-7]。而对于液体火箭发动机而言,燃烧不稳定性问题一直是困扰其技术发展的难题。当发生不稳定燃烧时,燃烧室内压力振荡会给系统的敏感制导元件以及系统结构带来破坏性的影响[8]。因此,如何设计反馈控制器以改善燃烧过程的稳定性能,成为学者们关注的热点问题[9-11]。
文献[12-14]讨论了在状态反馈控制器作用下系统的镇定问题,但所给出的控制器都要求能够精确实现,不具有鲁棒性。在控制器的设计实现中,由于硬件和软件等原因,不同程度上或多或少都存在一定的不确定性[15]。当控制器参数存在摄动时,常规的鲁棒控制器表现出高度的脆弱性,从而造成闭环系统的性能下降甚至控制器失效。非脆弱控制[16]的提出,弥补了这一不足,它不仅考虑被控对象的不确定性,而且考虑控制器增益本身的不确定性,因而更具适应性。文献[17-19]和文献[20-21]分别针对时滞系统的非脆弱H∞控制问题和非脆弱保性能控制问题进行了深入研究。在这些研究中,主要围绕如何降低所得结论的保守性和满足一定的性能指标而展开。因此,如何选取合适的L-K泛函和界定条件,进一步得到保守性更小的时滞相关条件从而设计有效的控制器便成为目前时滞系统稳定性分析与控制综合的首要问题。
本文中针对某液体火箭发动机的动态燃烧模型,在假定控制器增益存在加性不确定的条件下,提出一个形式简单、保守性更低的时滞相关有界实判据。该判据借助于一种新型的时滞分割法,把时滞区间分割成不均匀的两部分,针对每一分割区间构造新的L-K泛函,并采用新的积分不等式和交互式凸组合技术给出不包含任何多余参量的LMI形式结论。在此基础上设计了鲁棒非脆弱控制器。模拟结果表明,该控制器允许控制器增益存在一定范围内的摄动,改善了传统鲁棒控制器的镇定效果,具有更强的鲁棒性。
1 问题描述
考虑带有反馈伺服机构的单一燃料液体火箭发动机推进系统,系统描述见文献[9-10]。在假定非恒稳流动并考虑一致滞后情况下,整个系统的动态方程[1-2]为:
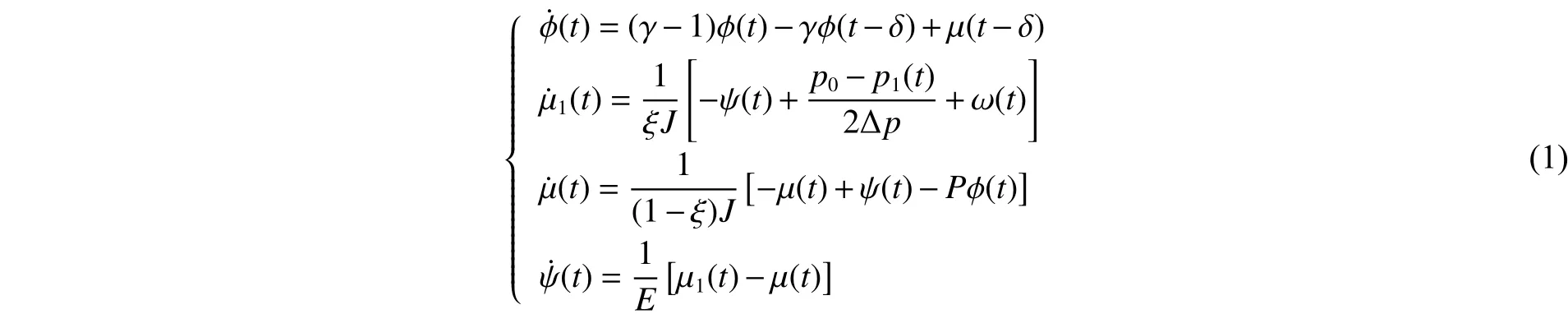
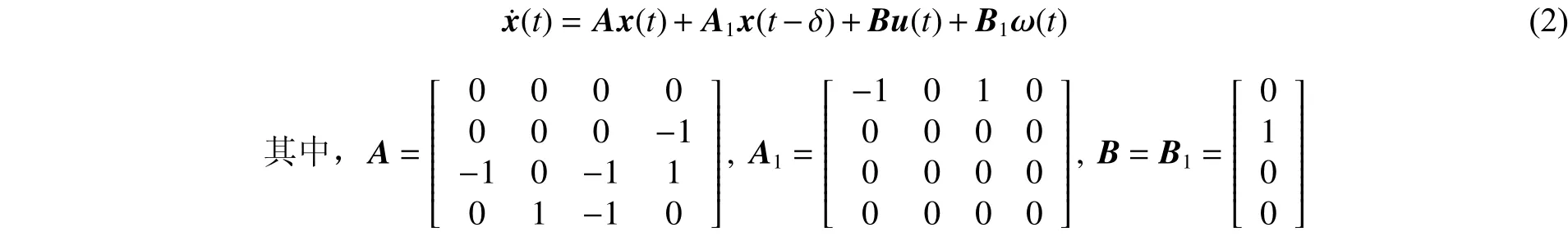
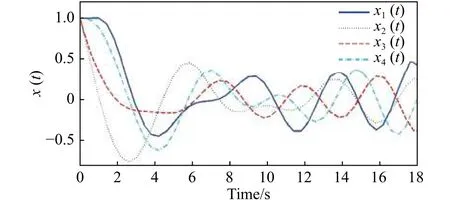
图1 燃烧室燃烧过程的自由运动曲线Fig. 1 Free motion of combustion in chambers
针对系统(1)定义如下性能指标
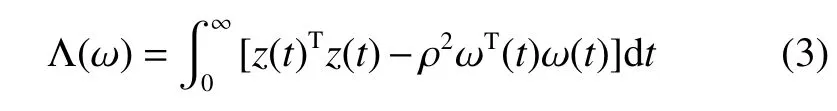
为了方便稳定性判据的证明,现将下一步需用到的引理归纳如下:
引理1[4]。假定任意的正定矩阵,标量和向量函数:,则有以下不等式成立:
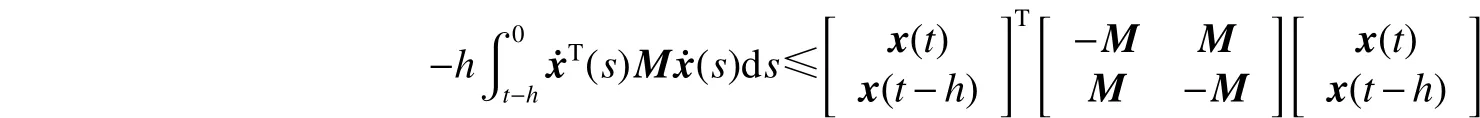
引理2[6]。假定任意的正定矩阵,标量h>0和向量函数:,则有以下不等式成立:
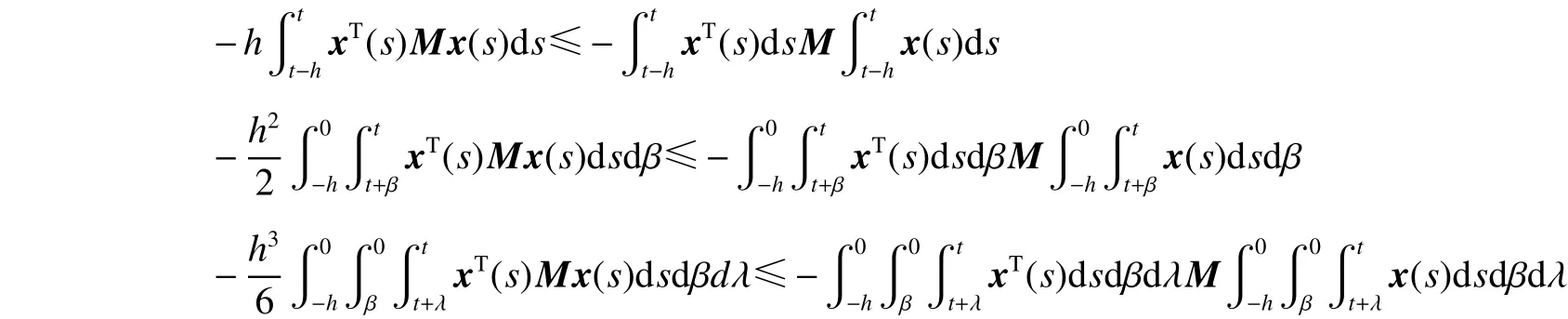
引理3[7]。假定任意的正定矩阵,标量,,向量函数:,则有以下不等式成立:
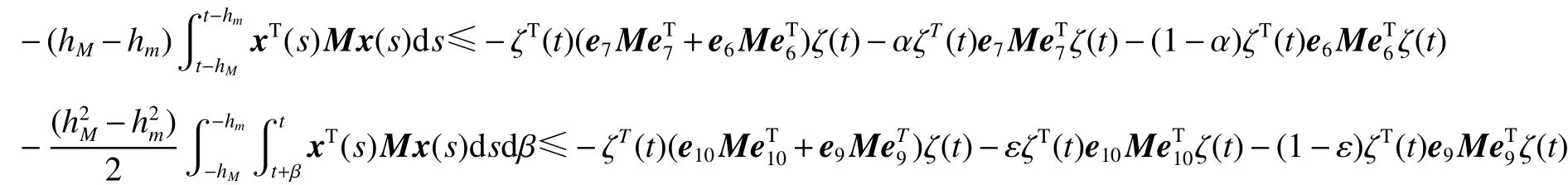
式中:

引理4[21]。给定适当维数的矩阵和,则有,对任意满足的成立的充要条件是存在标量,使得:
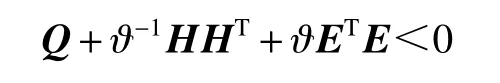
2 时滞相关有界实判据
针对系统(1)~(2),考虑如下一类具有区间变时滞的线性系统:

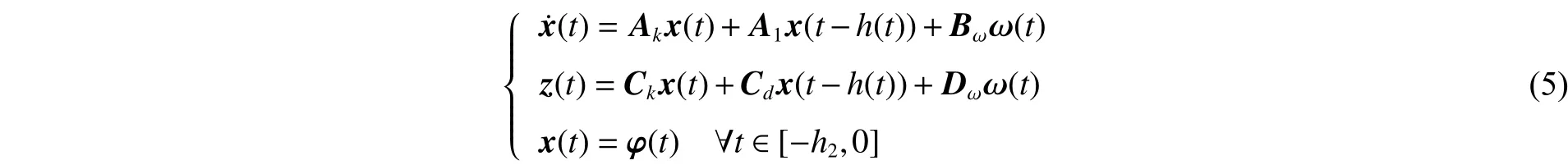
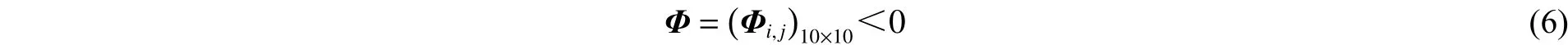
则系统(5)在非脆弱控制器(3)的作用下不仅渐近稳定,而且在零初始条件下具有给定的扰动抑制水平。
式(6)中:

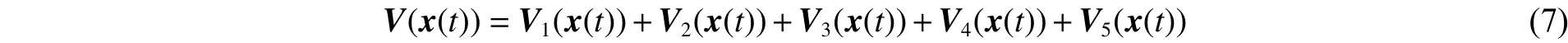
式中:

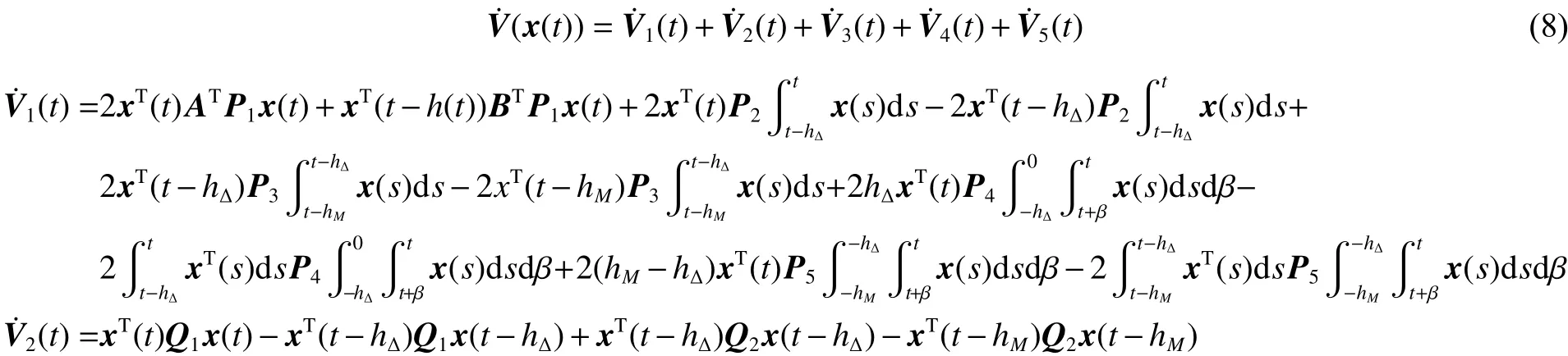
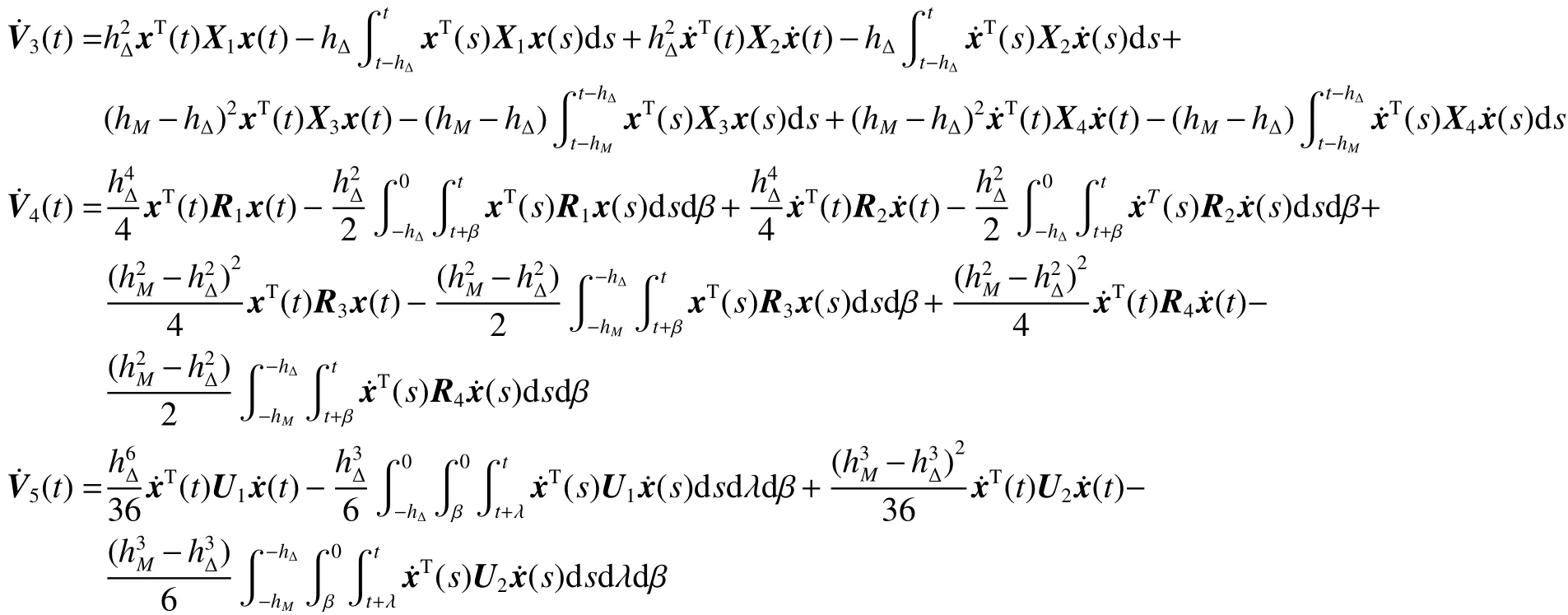
由引理1与引理2可得:
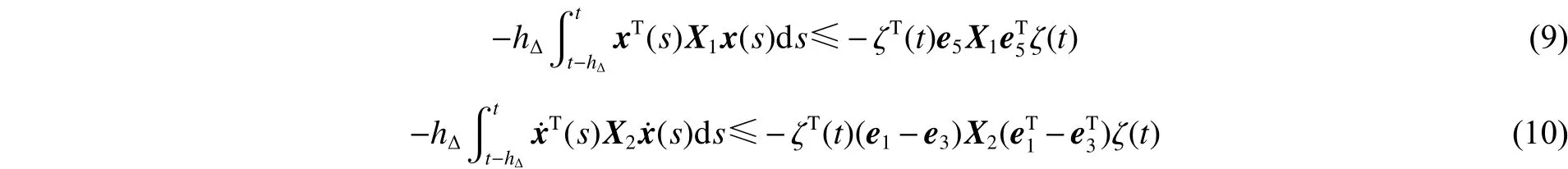
式中:
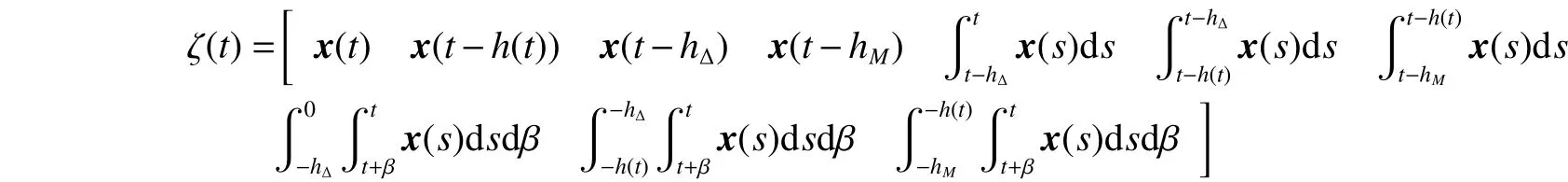
由引理3可得:
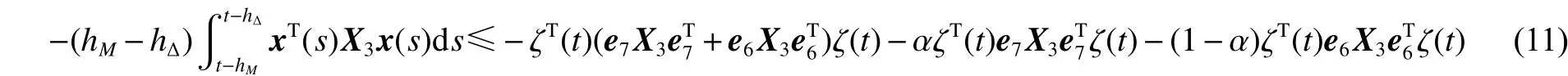
同样可以得到:

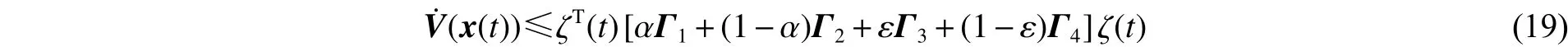
式中:
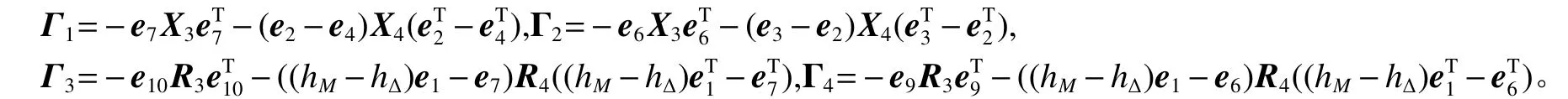
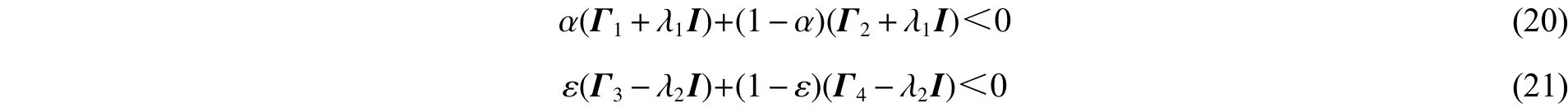
即
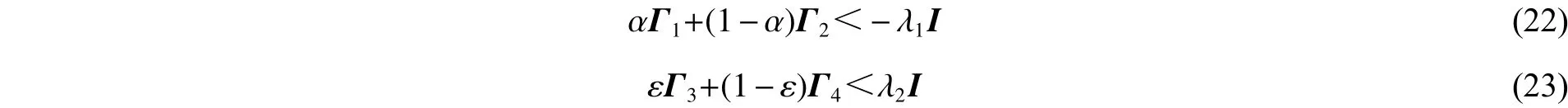
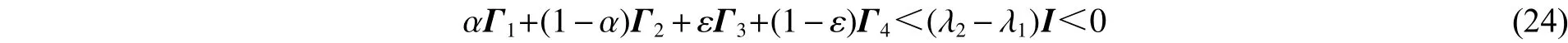
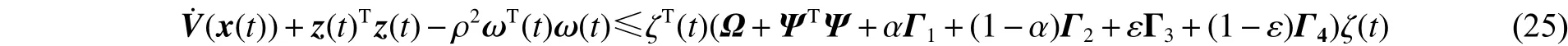
如果
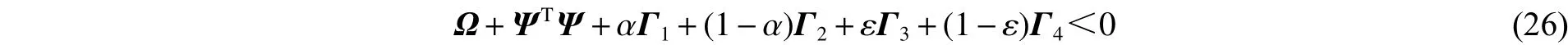
那么
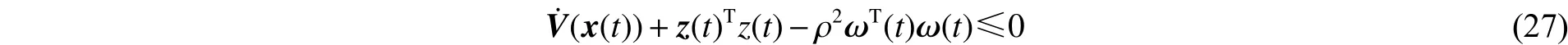

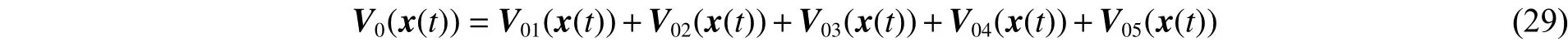
式中:
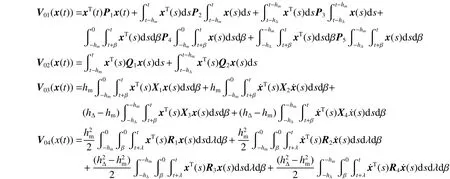
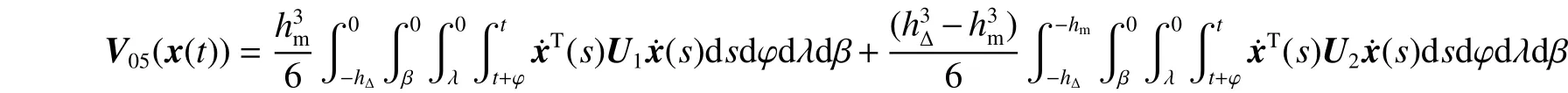
式中:
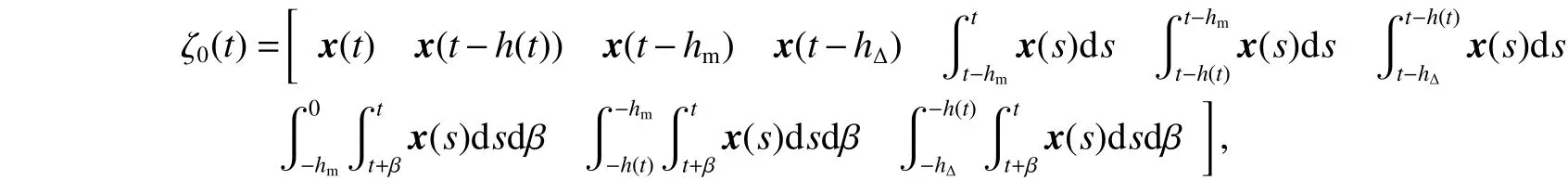

式中:
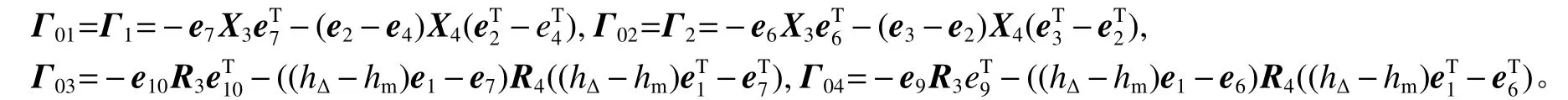
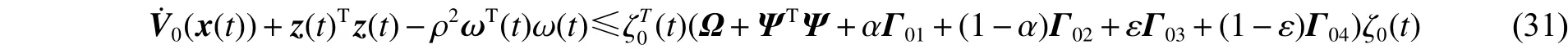
如果
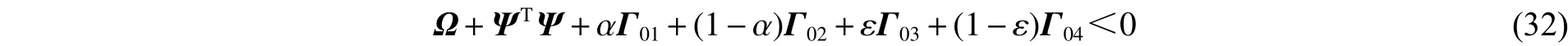
那么
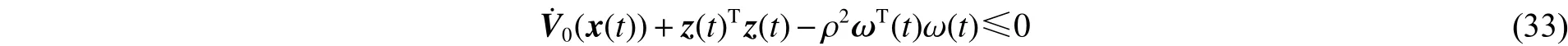
对式(19)或式(30)应用引理3,则其等价于式(6)。证毕。
针对式(1)~(2)描述的系统,考虑如下一类不确定时滞系统:
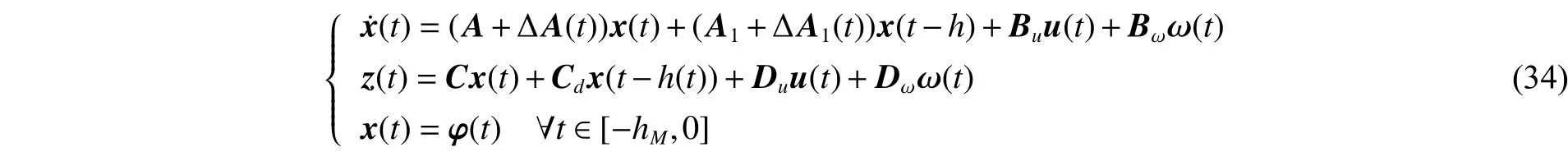
针对系统(34),本节在上一节有界实判据的基础上,给出非脆弱控制器的设计方法。
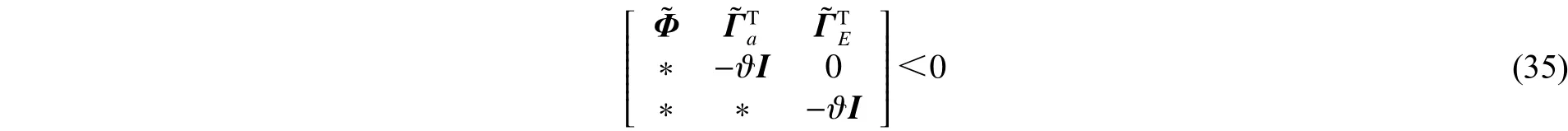
则不确定系统(34)在非脆弱控制器(3)的作用下不仅渐近稳定,而且在零初始条件下具有给定的扰动抑制水平,且控制器增益。
式中:
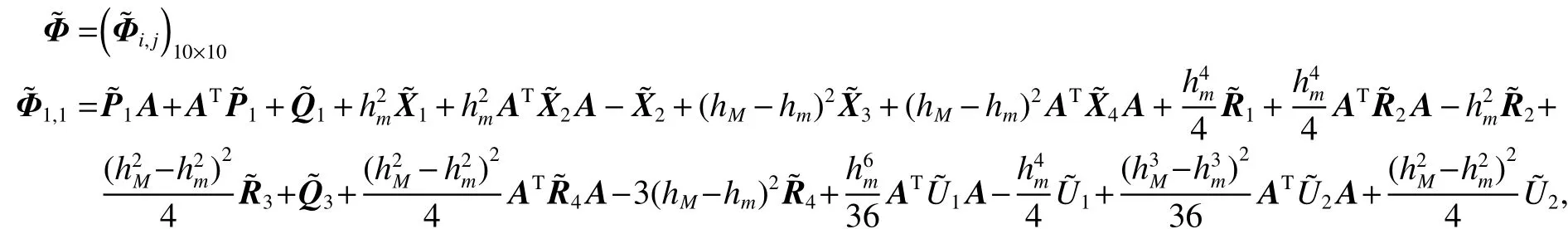
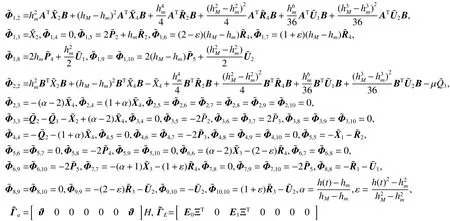
证明:由于定理1中式(6)给出的条件为非线性矩阵不等式,不能直接得到控制器的解。下面给出控制器的设计方法,首先将式(6)中的不确定项(即含项)分离,即

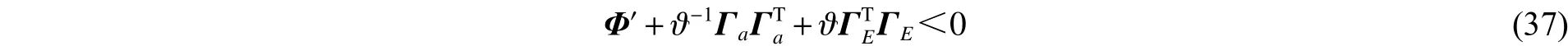
进而对式(37)应用Schur补可得
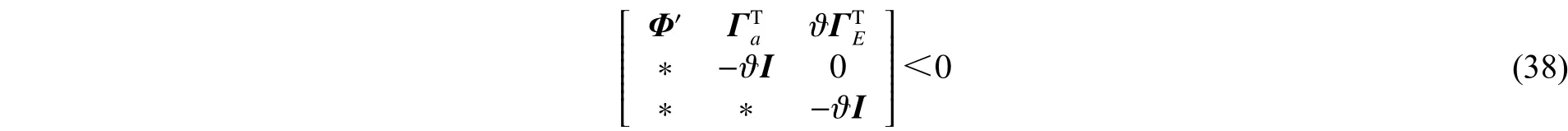
4 火箭发动机燃烧过程仿真
4.1 自由系统稳定性能分析
MADB (maximum allowable delay bound) 定义为保证系统稳定的最大允许时滞上界值,是时滞系统稳定性结论保守性最普遍的衡量标准;MAPI (minimum allowable performance index) 定义为保证系统稳定的最小允许性能指标值,是时滞系统在零初始条件下所具有的扰动抑制水平的衡量标准。
下面考虑一类具有区间变时滞的线性系统,形如式(1)所示,其系统参数如下:

表1 不同的H 性能指标ρ,模拟给出的MADB值hMTable 1 The maximum allowable delay bound hM for a given ρ
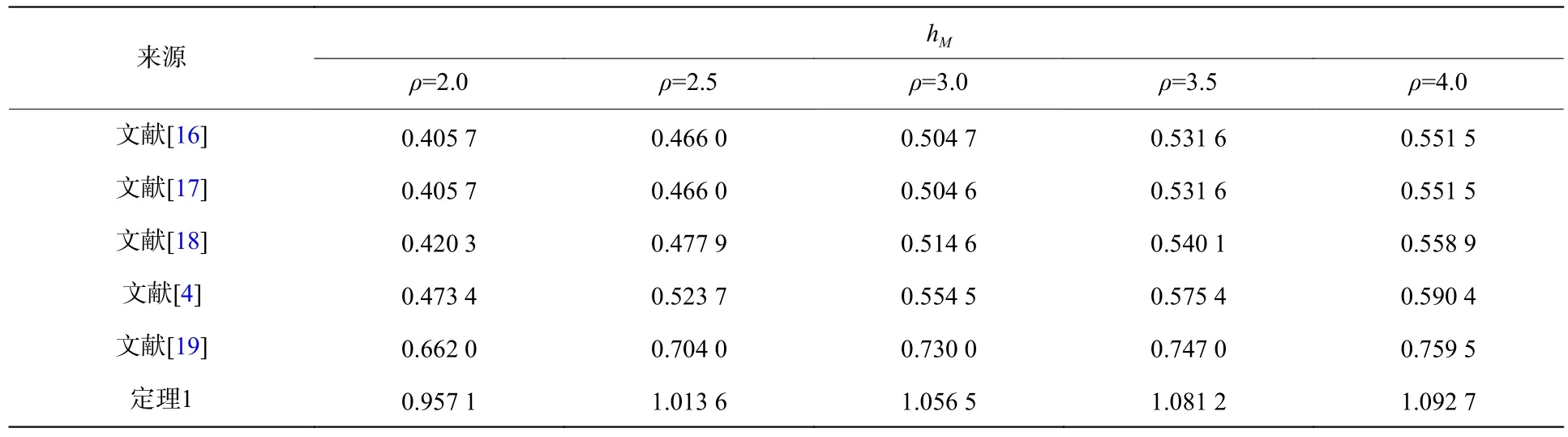
表1 不同的H 性能指标ρ,模拟给出的MADB值hMTable 1 The maximum allowable delay bound hM for a given ρ
hM ρ=2.0 ρ=2.5 ρ=3.0 ρ=3.5 ρ=4.0文献[16] 0.405 7 0.466 0 0.504 7 0.531 6 0.551 5文献[17] 0.405 7 0.466 0 0.504 6 0.531 6 0.551 5文献[18] 0.420 3 0.477 9 0.514 6 0.540 1 0.558 9文献[4] 0.473 4 0.523 7 0.554 5 0.575 4 0.590 4文献[19] 0.662 0 0.704 0 0.730 0 0.747 0 0.759 5定理1 0.957 1 1.013 6 1.056 5 1.081 2 1.092 7来源
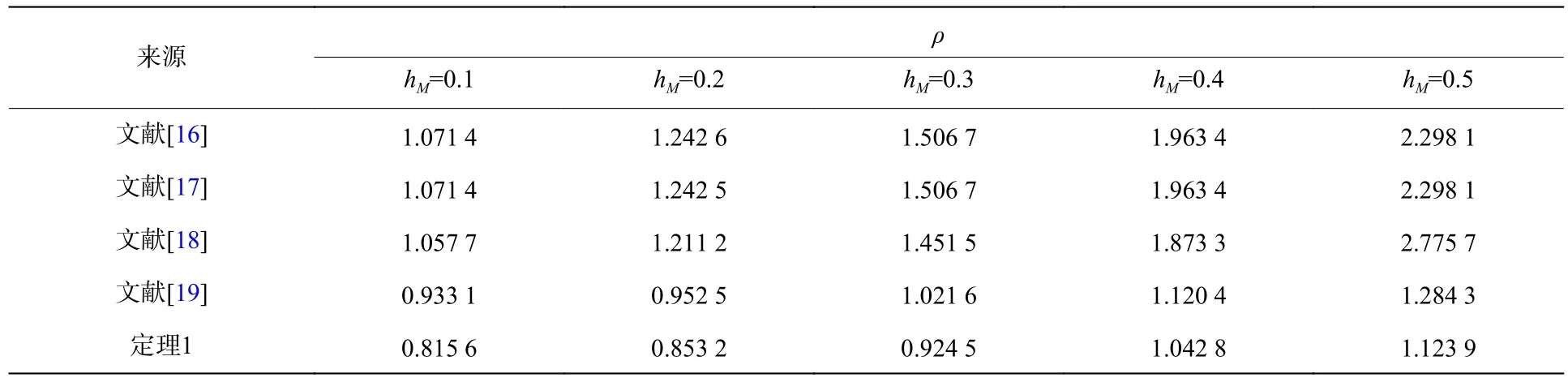
表2 不同的MADB值hM,仿真给出的MAPI值ρTable 2 The minimum allowable performance index ρ for a given hM
4.2 参数摄动的鲁棒性
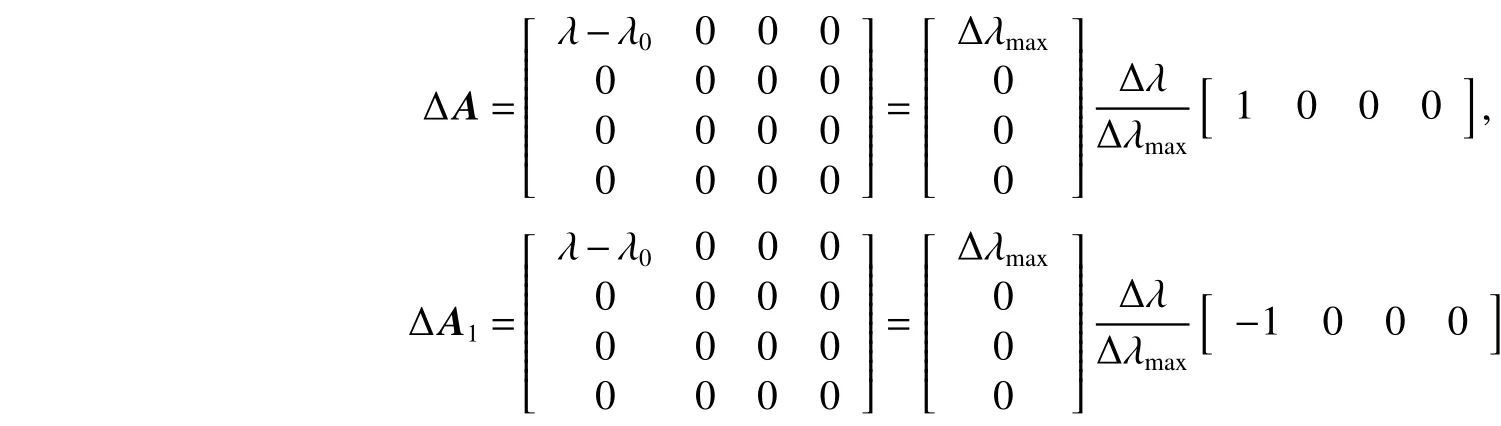
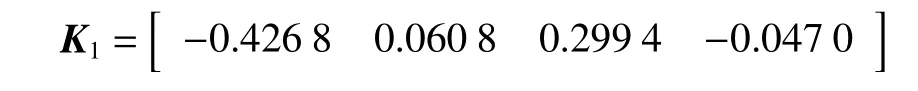
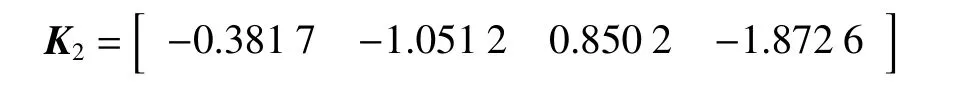
将非脆弱控制器代入燃烧过程方程,系统的状态响应曲线如图2所示。

图2 非脆弱H∞控制器作用下系统的状态响应Fig. 2 Response of system under non-fragile H∞ controller
从图2可知,当系统参数和控制器增益存在不确定性时,该系统不仅具有鲁棒性而且是非脆弱的,燃烧过程得到了较好的镇定,系统能满足一定的性能指标要求,控制器具有足够的调节余地,系统的可靠性更高。
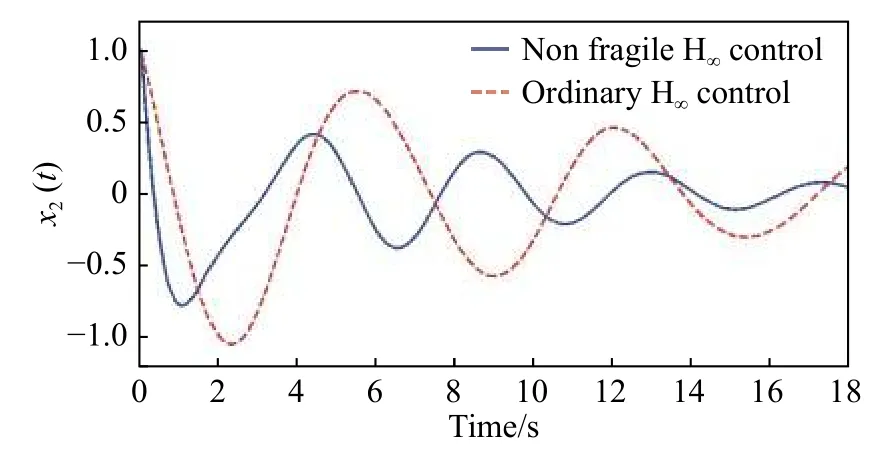
图3 不同控制器作用下系统状态的响应Fig. 3 Response of under different controller
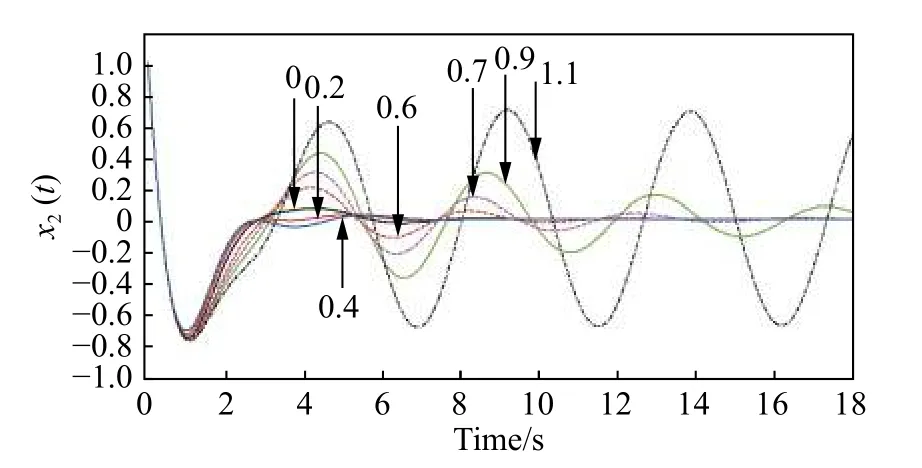
图4 控制器对时滞参数的鲁棒性Fig. 4 Robust performance of controller to variation of
5 结 论
(1)通过构造包含四重积分项的L-K泛函以及采用新颖的积分不等式来界定交叉项,给出了保证燃烧过程稳定并具有给定性能指标的时滞相关有界实引理;
(2)在有界实引理的基础上,通过求解线性矩阵不等式的可行解来获得控制器的参数化表达式,进而设计了一种无需参数调整并易于求解的鲁棒非脆弱控制器;
(3)通过仿真实例对比验证了所提出的时滞相关有界实引理的有效性以及所设计的鲁棒非脆弱控制器的优越性。
从图4可以清晰地看到,在本文设计控制器作用下,当时滞参数δ逐渐增大时,燃烧过程中状态变量x2(t)逐渐趋于不稳定,但是在内,燃烧过程状态变量x2(t)仍然是可镇定的;需要说明的是,上面的模拟是在并且的情形下进行的,也就是说本文所设计控制器增益值满足一定摄动性,因而提升了燃烧过程的可靠性和鲁棒性。

