高饱和黏土中爆炸波作用下直埋聚乙烯管的动力响应*
钟冬望,龚相超,涂圣武,黄 雄
(武汉科技大学理学院力学系,湖北 武汉 430065)
聚乙烯(polyethylene, PEPE)管以其优良的性能被广泛应用在燃气输运、给水排水等生命线工程中,是国际上使用成熟的和中国现阶段大力推广使用的管道。爆破技术是一种工程上常用的经济高效的施工技术手段,然而频繁的爆破作业带来的负面效应也突现出来,爆破中所产生的冲击和震动效应对周边的地下管线可能造成安全上的隐患。因此,准确计算爆源和管道的安全距离,消除爆破冲击对管道的潜在威胁,对工程爆破的合理设计和安全施工至关重要。另一方面,过于保守的计算和标准可能导致不必要的严苛的爆破设计方案,甚至从根本上否定了选用爆破技术进行施工的可能性,这样无疑会增加施工难度和项目成本。
目前,对于爆炸波作用下的埋地管道的实验和计算,一类是由Dowding[1]基于Newmark建立的模型提出的计算式:
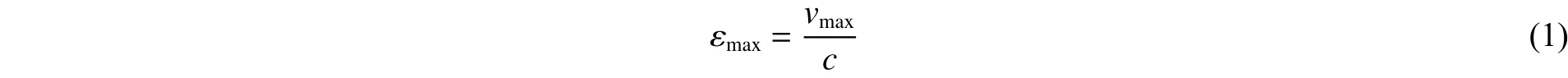
式中:εmax为管道最大应变,vmax为土体粒子最大振动速度,c为波速。
另一类是基于大量的模型和原型实验数据,最初由Esparza等[2]通过相似理论推导出的经验公式:
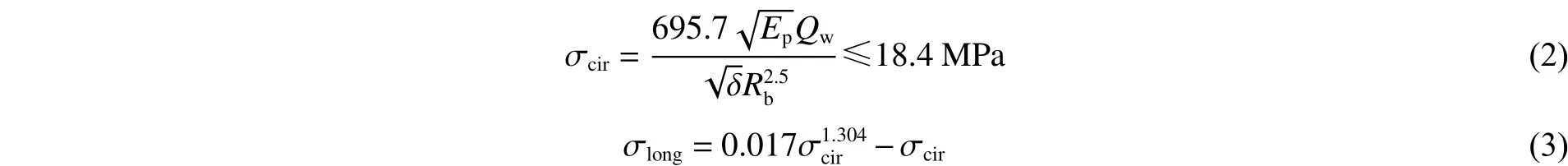
式中:σcir和σlong分别为管道环向应力和轴向应力,Ep为管道杨氏模量,δ为管道壁厚,Rb为爆心距,Qw为等效药量。
式(1)中假设爆炸波是具有恒定幅值的平面波,通过波动方程推导出的解析解,是假设管土共同运动且无相对滑移下的计算公式。显然这是一种粗略的计算方法,优点是计算简单。式(2)和式(3)是纯经验性的,在与实验环境类似的场地条件下计算的结果无疑是准确的,但其应用范围受到限制。后来,Siskind等[3]进行了一系列爆炸波作用下柔性管道动态响应的原型实验,实验结果表明:即便是在单响药量很大的情况下,管道动力响应水平也很低,诱发的动应变也很小。Kouretzis等[4]采用3D薄壁圆筒模型,将爆炸波简化为简谐荷载,推导了地表爆炸荷载下埋地管道应变的计算公式,并提出了简化计算式,这是一种半理论半经验的公式,其适用范围也值得商榷。
本文中,采用动态应变测试系统、压电陶瓷测试系统和爆破振动测试系统,对高饱和黏土中爆炸波作用下PE80管道进行动态应变测试、动态压力测试和管体及地面的振动测试。以期得到的一些实验结果和结论可以对现有成果做有益的补充。
1 爆炸波下埋地管道应力的量纲分析
影响管道动态应力分布的因素很多,各变量之间的关系也非常复杂,要建立精确的函数描述各因素综合作用是非常困难的。因此,采用相似理论,对各变量进行量纲分析,基于实验数据来确定经验公式不失为一种好的解决方法,具有工程实用价值。
1.1 爆源和爆炸波的土中传播模型
实验中爆源为土中小药量球形药包耦合装药,本文中可将其简化为点源,并假设土体中药量为Q的炸药爆炸是瞬时的,忽略炸药的反应过程。关心的重点是:冲击波区以外爆心距为Rb土体的振动速度峰值vmax。设土体为半无限的空间,均匀且各向同性,密度为ρs,纵波的速波为c,这2个参数分别代表土壤的惯性和压缩效应。做量纲分析的4个参数函数表达式如下:
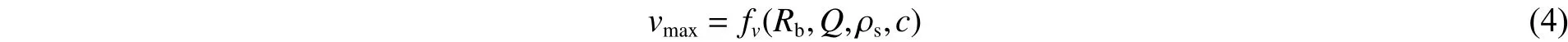
应用π定理,可得如下关系式:
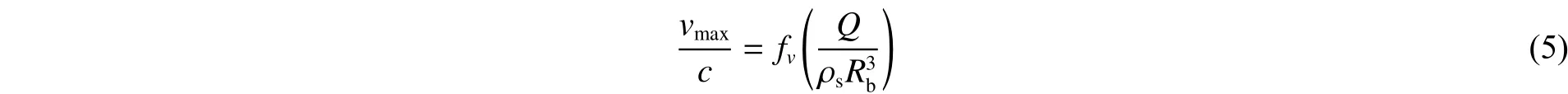
对于本实验,视纵波波速和土体密度为常数,因此可采用萨道夫斯基公式:
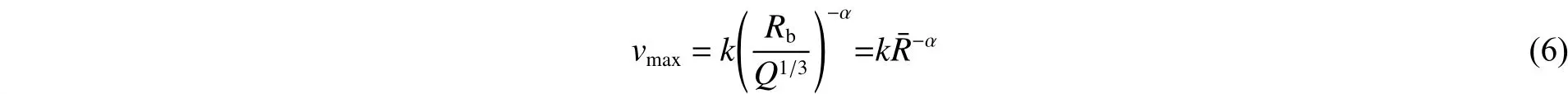
1.2 管道的应变模型
管道外径为D,壁厚为δ,密度为ρp以及弹性模量为Ep,受到粒子速度为v的爆炸波的冲击作用,爆心距为Rb,土壤的密度为ρs,土体压缩模量为Es,纵波波速为c。爆炸波引起的管道变形为线弹性变形,径向和轴向最大应力为σmax。这些变量所表征的影响因素包括荷载因素、管道及土体的惯性效应和压缩效应,以及管道截面的几何性质。以函数形式表示的管道外表面的应力为:
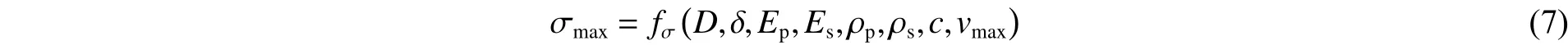
用无量纲形式表达,可以将式(7)改写成:
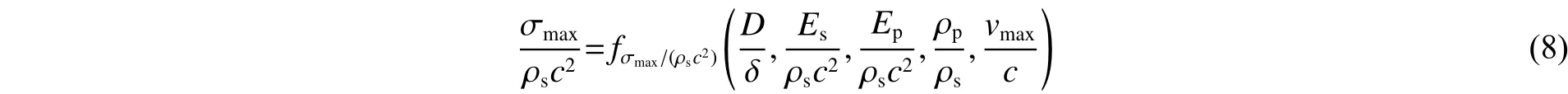
函数的具体形式是未知的,只有通过实测数据才能够确定管道的最大径向和纵向应力公式。对于本次实验参数 D、δ、ρp、Ep、ρs、Es、c确定下来后,只剩下一个变量 vmax。依据式 (6),本文中采用类萨氏公式形式的方程,由实验数据检验其合理性。由于实验直接测的是管道外表面的应变,管道的外表面可简化为平面应力状态,在线弹性变形范围内,应力应变关系遵循广义胡克定律,因此对于管道最大应变εmax,本文中采用如下幂函数形式:
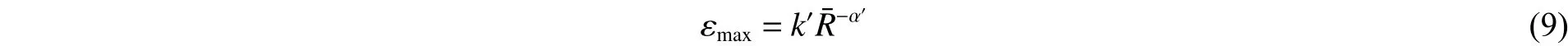
式中:k′和α′为反映场地、装药、管道等因素综合影响的参数,α′为衰减指数。
2 PE管和实验场地参数
2.1 PE管参数
实验对象采用黑色PE80材料的给水管,公称外径为315 mm,公称壁厚为18.7 mm,最小强度要求为8 MPa,公称压力为0.8 MPa。由于中高密度的聚氯乙烯材料随加工工艺不同力学性能变化很大,因此根据国家标准GB/T 8804-2003实验规范[5],采用同批次管道材料制成b类标准试件,使用MTS公司生产的型号为CMT5105的电子万能试验机和Y25/5引伸计开展材料拉伸实验,5次实验结果取平均值。图1为第3次实验数据图形,数据处理后PE管及材料参数分别为:总长度L=4.8 m,外径D=314.9 mm,厚度 δ=18.4 mm,密度 ρp=936 kg/m3,杨氏模量Ep=834.9 MPa,泊松比μ=0.40,强度极限σu=31.6 MPa,延伸率 ξ=116%。
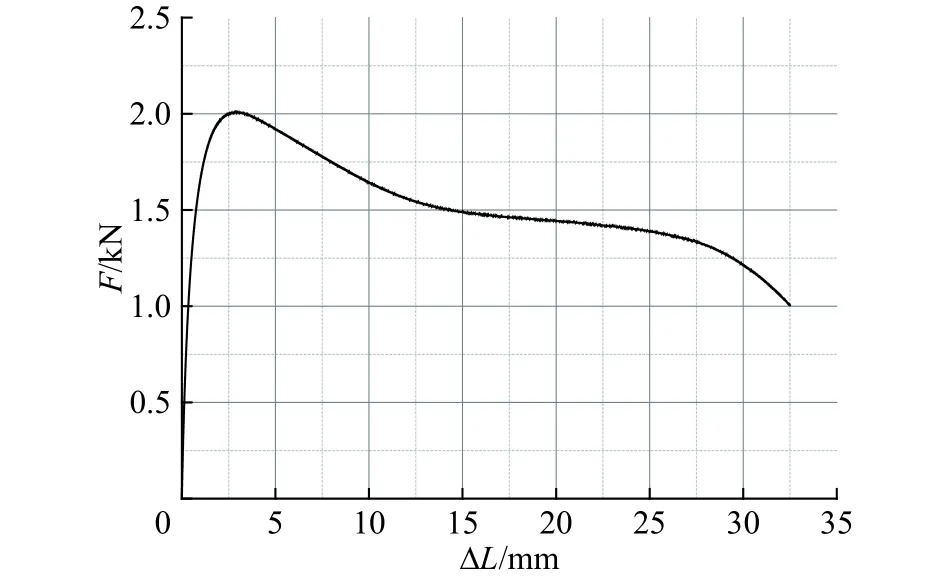
图1 拉力和绝对伸长的关系曲线Fig. 1 Relation between tensile force and absolute extension
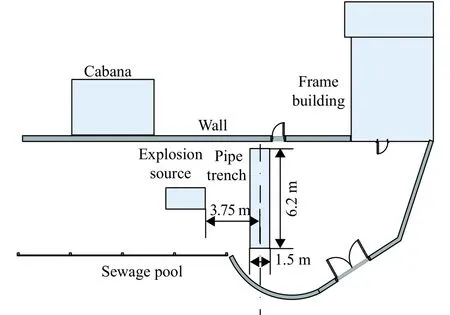
图2 实验现场示意图Fig. 2 Diagram of experimental site
2.2 实验场地参数
实验场地如图2所示,场地土介质为黄黏土。管道埋设实验场地紧临一个污水处理池,池边和直埋沟最近仅隔3 m,场地土的含水量随距地表深度变化增加很快,约2.5 m深以后土体呈淤泥状,不同深度土层参数变化很大。因此,采用中岩科技生产的SR-RCT声波测井仪,测试了实验场不同含水量土体的纵波波速,实验数据如表1所示。从实验结果可以看出:土层随着深度的增加,含水量增大,纵波波速相应增大。实验结果同已有文献实验数据相吻合:黏性土中含水量和纵波波速总体趋势是正相关的,在土体含水率较大时,纵波波速随含水率增大而增大[6]。

表1 不同深度土体纵波波速Table 1 Longitudinal wave velocities of soil at different depths
3 实验内容和过程
3.1 实验内容
管道动态应变测试是本次实验最重要的一项内容。普通大气环境下应变测试相对简单成熟,而待测管道直埋于黏土中,应变片工作在含水环境下,当前对防水应变片的研究很少,成熟的防水应变片产品也很少。具有代表性的是日本KYOWA共和KFWS小型防水箔式应变片,但该应变片多用于混凝土内部应变测试,且价格高昂,普适性低。因此,本次实验采用普通BX120-3AA型电阻应变片,用水中胶做防水处理[7]。其主要问题是:(1)保证应变片长时间浸泡在水环境下有效工作问题;(2)应变片的冲击防护层和防水涂层对测试结果影响的问题;(3)信号远距离传输抗噪声干扰问题。这些问题在前期辅助实验中得以解决。
采用压电陶瓷片(PZT)被动检测动态压力变化是本次实验的第2项内容[8],可用来校验实测动应变数据的有效性。本次实验中采用6片13 mm×13 mm×1 mm的矩形PZT发电片,用水中胶做防水涂层。管道上应变片和压电陶瓷片贴片位置如图3所示。
实验第3项内容为使用爆破振动测试仪,检测管道和地表土爆破振动速度,速度传感器布置在管道端部和管道3截面处的地表正上方。
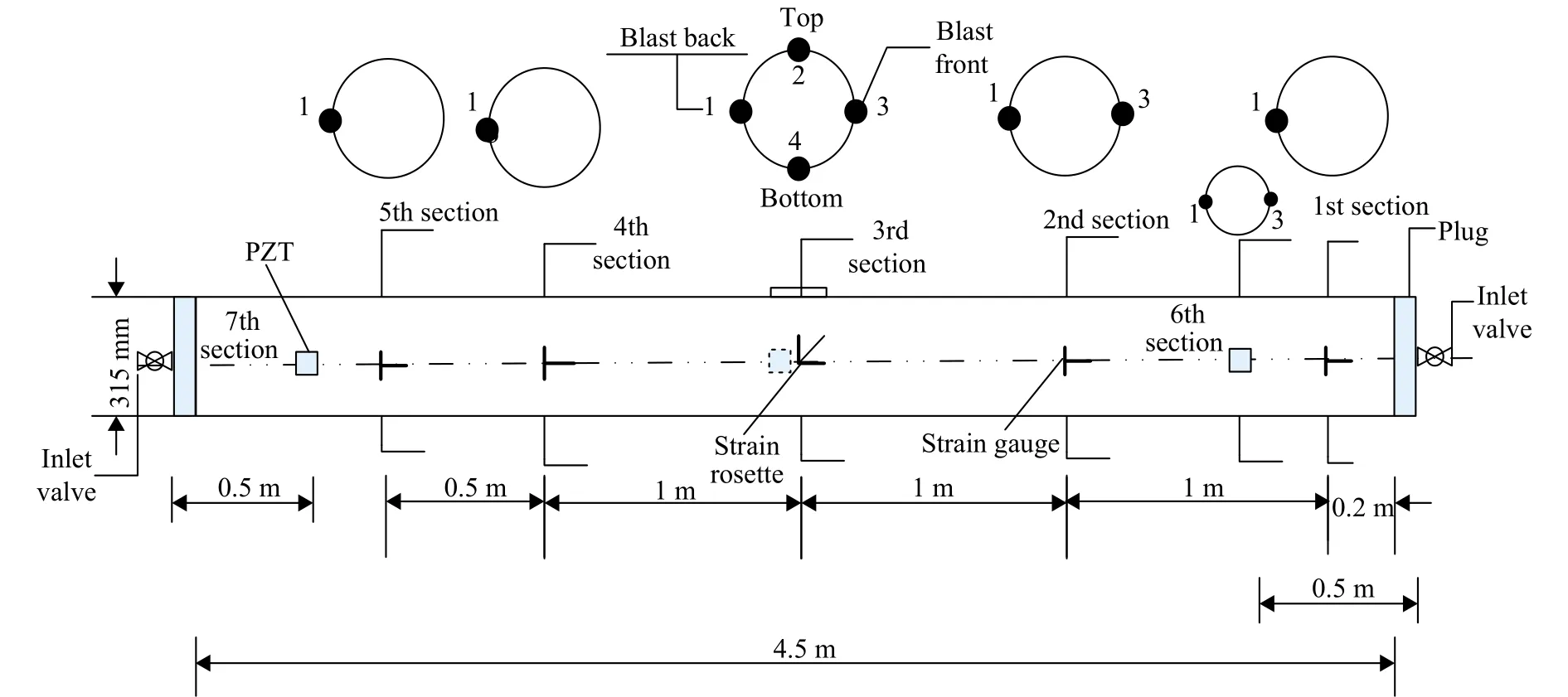
图3 管道贴片示意图Fig. 3 Location of strain gauges and PZT pieces on the pipe
3.2 实验过程
管道埋深为1.5 m,管道两端用砖砌成深井,方便排水和第2期加压实验时开关进气阀和进水阀,直埋沟抽水完毕后,沟底人工填土夯实,用一薄层细沙垫平。实验中,管道的5个截面9个测试点共贴有19个应变片(管道正中迎爆面的45°应变花算3个应变片,参看图3),使用8通道动态应变仪3台,其中2台为优泰公司出产型号为UT3408,最高采样频率为128 kHz,1台东华测试出产型号为DH5937,最高采样频率为20 kHz。实验过程中考虑到爆炸冲击过程历时较短,所有应变仪设置为最高采样频率。压电陶瓷片沿3个截面布片,迎爆面和被爆面各1片,共6片,桥盒采样频率设置为1 kHz。管道端部和管道正上方中部地表,采用型号为TC-4850爆破振动测试仪测振,采样频率为8 kHz。爆源和管道中心线处于同一水平高度,距管道3截面处中心线垂直距离为3.75 m。2#岩石乳化炸药,球形药包,耦合装药,装药严格按实验前制定的标准执行,一发导爆管雷管引爆,药室装药后覆土至少50 cm,然后上压沙袋,炸药埋深满足:
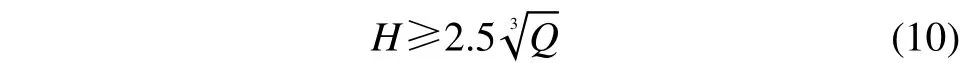
以消除自由面的影响[9],式中H为装药中心到自由面的计算距离,Q为药量。本次实验为第一期空管实验,管内压力为一个大气压,随药量变化共做7炮,药量分别为 50、75、100、125、150、175、200 g,埋深和爆心距如图4所示。
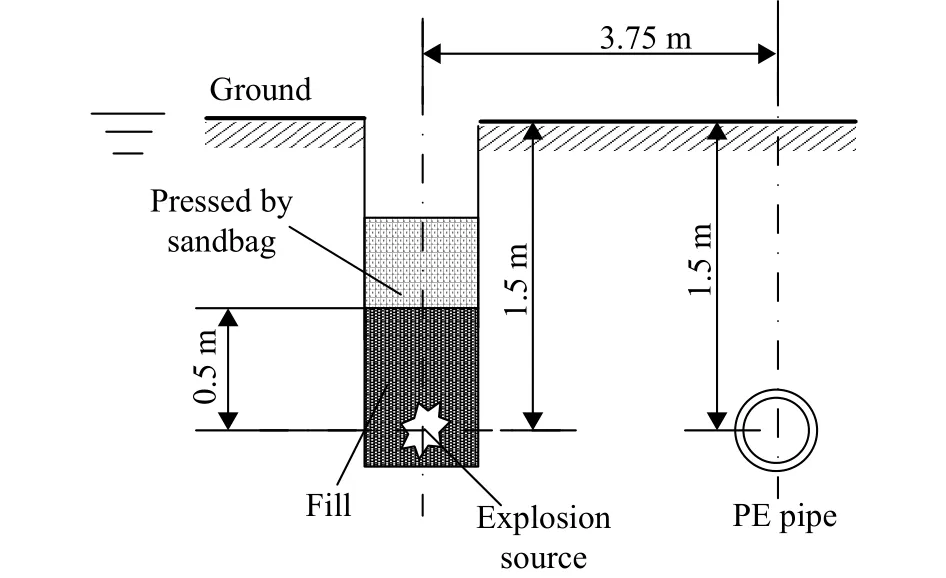
图4 爆源和PE管位置示意图Fig. 4 Location of PE pipe and explosion source
4 实验结果和分析
4.1 管道动态应变数据和分析
4.1.1 动态应变数据
典型应变时程曲线如图5所示,图5(a)为DH5937采集到的原始信号,图5(b)为UT3408采集低通滤波后的信号。UT3408应变仪采样频率高,未设置截止频率滤波,因此噪声信号干扰严重。后经频谱分析得知,由于土体对管道的强阻尼作用,有效信号主要集中在低频段(0~500 Hz),爆炸波冲击下管道振动持时约300 ms。对比两者波形和通过频谱分析可知,20 kHz采样频率也可以满足测试需求。值得指出的是:有效信号之前有一个明显的干扰信号,为完美的压缩波波形,持时约0.3 ms;后来查明该信号是炸药起爆时的高压电流脉冲信号。截面1和截面5由于应变片损伤和仪器调试原因大部分数据未测到或舍弃,截面4和截面2具有对称性,因此剔除数据不完整应变信号后,得到各测点有效的最大拉应变和压应变数据如表2~3所示,位置标注中,第1位为截面号,第2位方位号,参照图3。
4.1.2 动应变数据
从总体看,正对爆源的截面3,无论是迎爆面还是背爆面的中心测点(测点3和测点1),最大的环向压应变绝对值都大于环向拉应变,轴向拉应变和压应变绝对值大致相当;管道顶部和底部(测点2和测点4),环向拉应变大于压应变绝对值,轴向压应变绝对值大于拉应变,45°方向应变值相对较小。当比例距离较小时,环向应变最大值(下文中压应变最大值均指绝对值最大)比同测点轴向应变最大值要大。需要指出的是:各截面各测点之间的峰值拉应变或峰值压应变由于爆炸波传播动态效应,有时并不是同一时刻达到极值,往往有几毫秒的间隔,下面计算中忽略这种差别,按最不利状态处理。根据式(6)和式(9),对具有代表性的测点应变峰值随比例距离衰减做回归处理,如图6~8所示。本文中计算比例距离时,直接采用实验所用的2#岩石乳化炸药药量,未做TNT当量转换,本次实验的比例距离在6~11 m/kg1/3之间。两者计算结果仅相差一个比例系数,并且在本次实验条件下2种计算结果均处于爆炸波同一分区内。从回归后衰减曲线可以看出:同一测点的最大拉压应变以及2个截面各测点轴向和环向最大应变均和比例距离成良好的幂函数指数形式衰减关系。回归后决定系数在0.91~0.97,环向应变的衰减指数(绝对值,下同)明显大于轴向应变衰减指数。环向衰减指数在-6.8~-5.7,轴向衰减指数在-3.9~-3.2。对于相同截面不同测点衰减指数是不同的,近爆截面衰减指数绝对值大,远爆截面衰减指数小。通过图6(a)、图7(a)和图8可以看出:同一截面迎爆、背爆、顶部和底部测点的环向应变,不同截面迎爆测点的环向应变的差值随着比例距离增加而减小;比较图6(b)和图7(b)可知:轴向应变这种差值几乎不随比例距离变化而变化。产生这种差异性的原因是:环向应变同管道截面的局部变形有较强的相关性,而轴向应变受管道整体变形影响更大的缘故。图9比较了截面2和截面3测点3的轴向应变,可以看出两者数值上大致相当,这也表明轴向变形和整体变形的强相关。
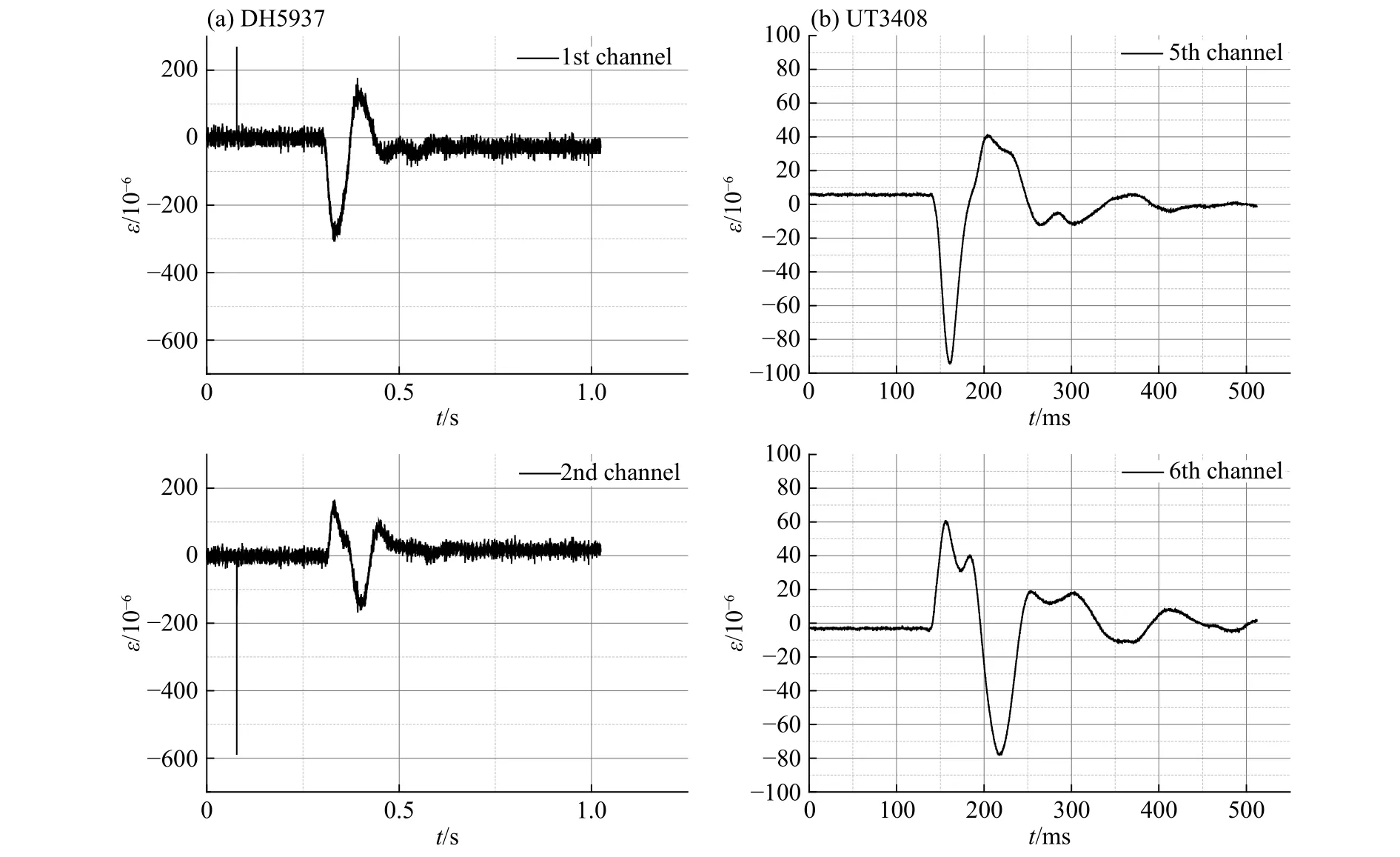
图5 两种应变仪采集的典型信号Fig. 5 Typical signals detected by DH5937 and UT3408
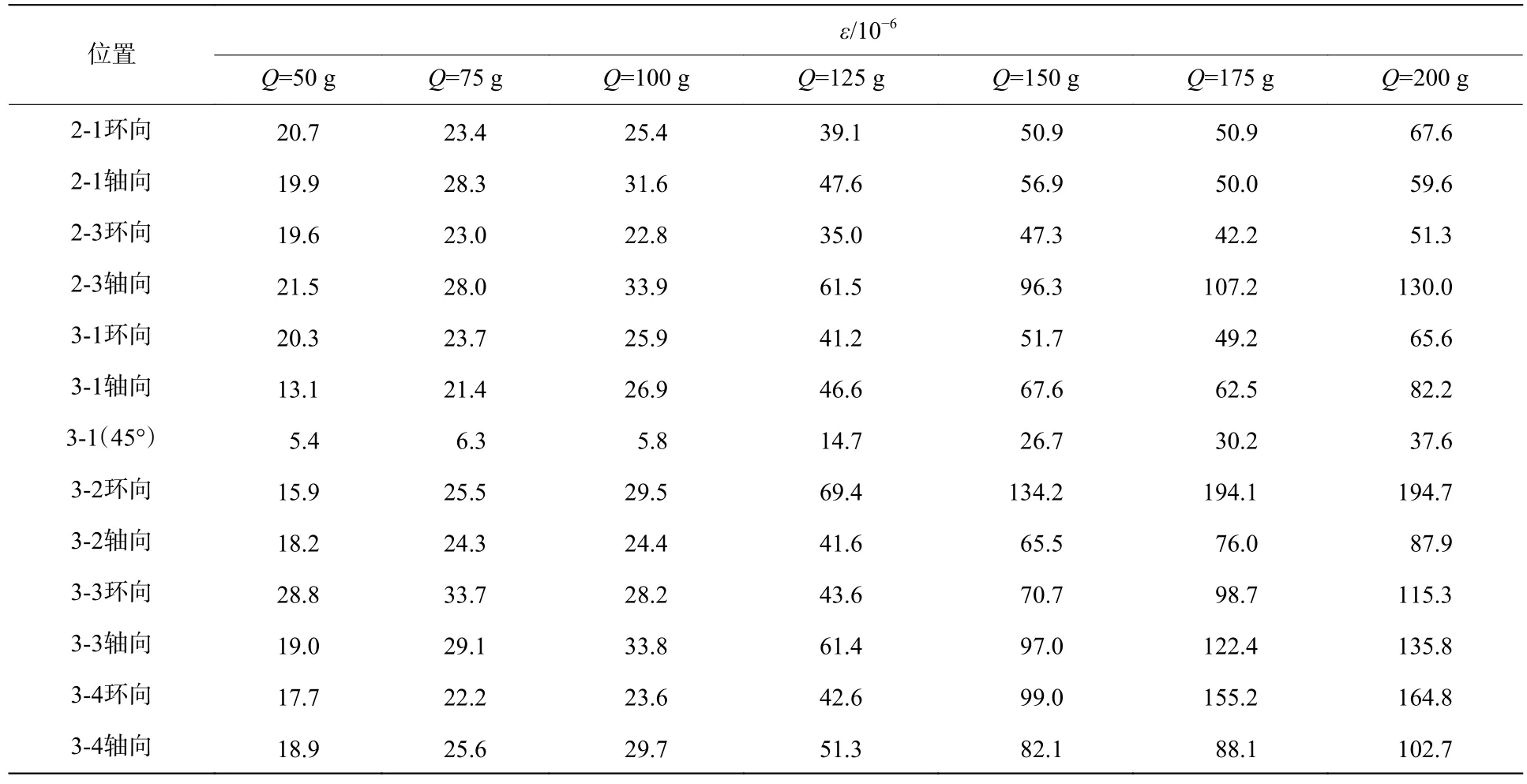
表2 不同药量下各测点最大拉应变Table 2 The maximum tensile strain at each measuring point under different explosive charges
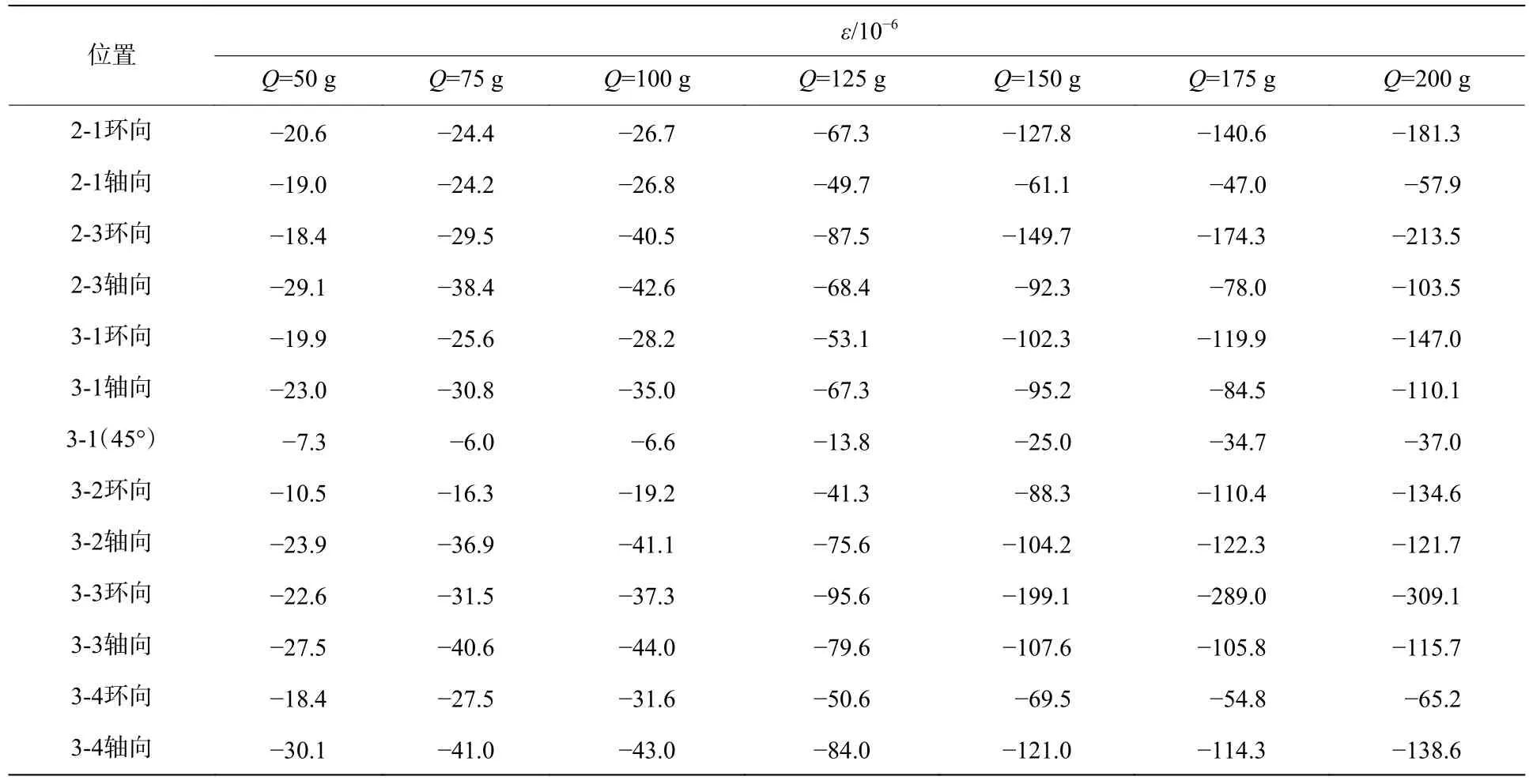
表3 不同药量下各测点最大压应变Table 3 The maximum compressive strain at each measuring point under different explosive charges

图6 位置3-1和3-3的环向和轴向最大压应变衰减曲线Fig. 6 The maximum hoop and axial strains at positions 3-1 and 3-3 varying with scaled distance
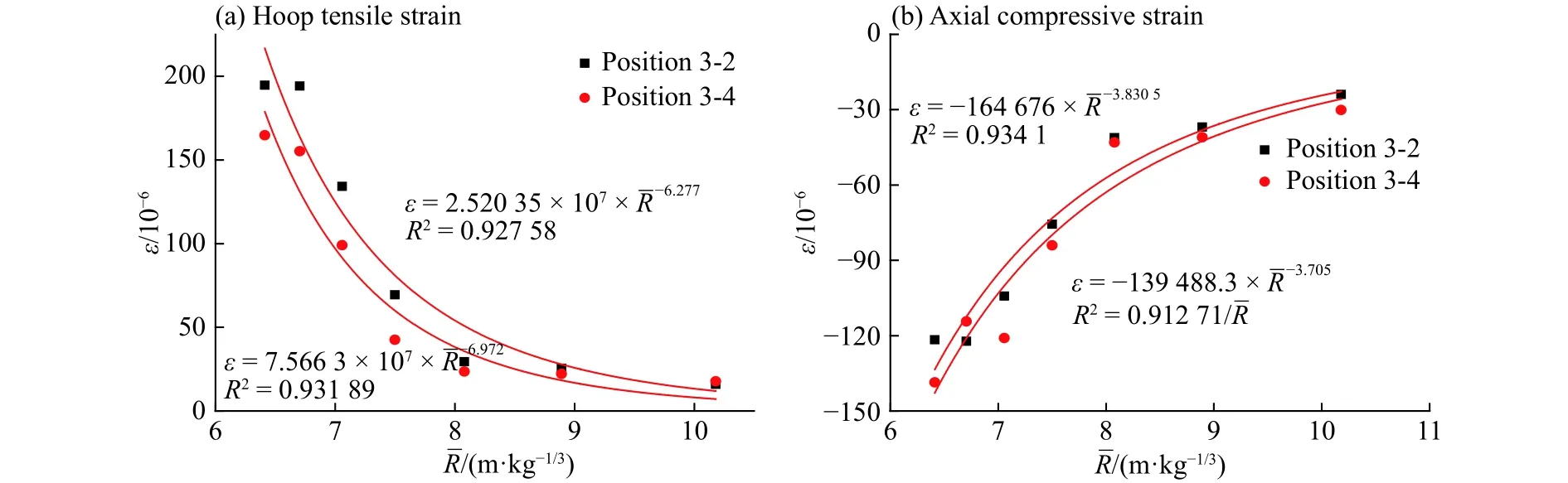
图7 位置3-2和3-4的环向和轴向最大应变衰减曲线Fig. 7 The maximum hoop and axial strains at positions 3-2 and 3-4 varying with scaled distance
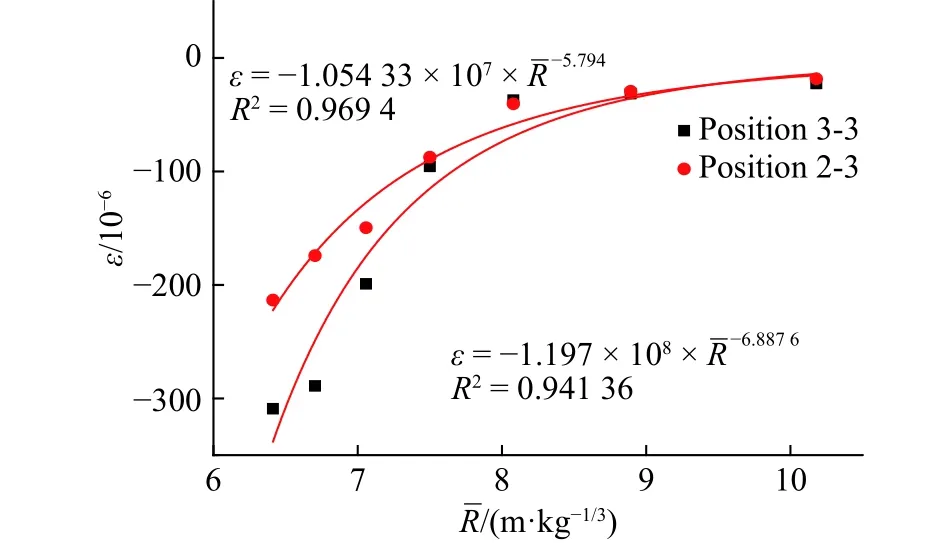
图8 位置2-3和3-3的环向最大压应变Fig. 8 The maximum hoop compressive strains at positions 2-3 and 3-3
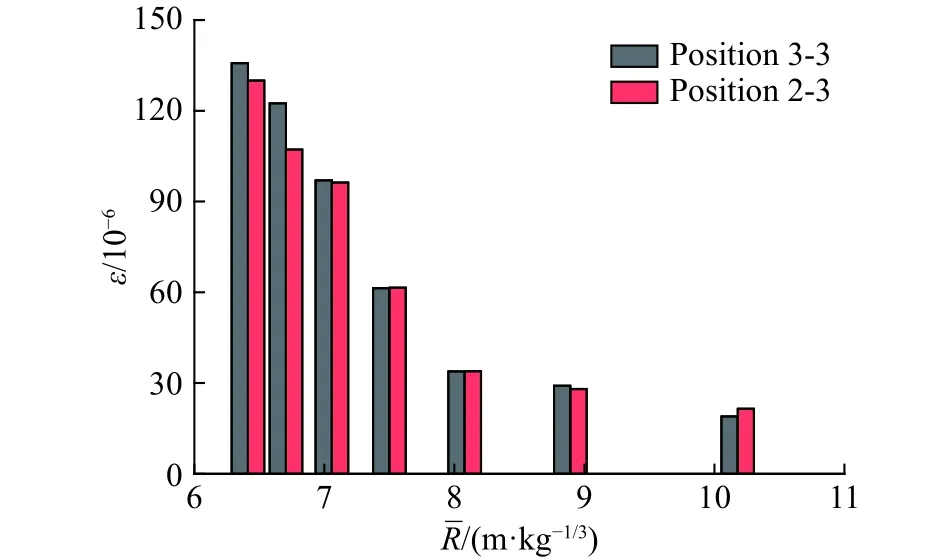
图9 位置2-3和3-3的轴向最大拉应变Fig. 9 The maximum axial tensile strains at positions 2-3 and 3-3
实际上爆炸波在土介质中传播时,随着爆心距的不同具有不同的应力幅值和加载率。据库特乌佐夫的研究成果:比例距离时,岩土中爆炸波以纵波为主,当时,波形开始转换,面波成分逐渐增加;当时,爆炸波以面波为主[10]。本次实验中爆炸波正处于纵波向面波波形转换分区内,因此各测点的最大拉、压应力相对大小转换的特点非常明显。如图10所示,取截面2测点1的最大拉、压应力绝对值做对比,随着比例距离增大,两者差值逐渐较小直至幅值大致相当;如图11所示,取截面3测点1的环向和轴向应变,随着比例距离的增大,两者的相对大小发生转变,从环向比轴向应变大转变到轴向比环向应变大;当比例距离较小的时候,2个截面环向最大压应变相差较大,随着比例距离增大,两者差值逐步减小直至基本消失,这也是爆炸波波形演化较充分的结果。
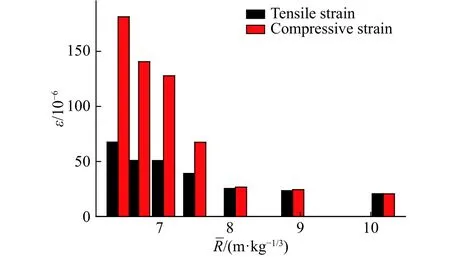
图10 位置2-1环向最大拉和压应变Fig. 10 The maximum hoop tensile and compressive strains at position 2-1
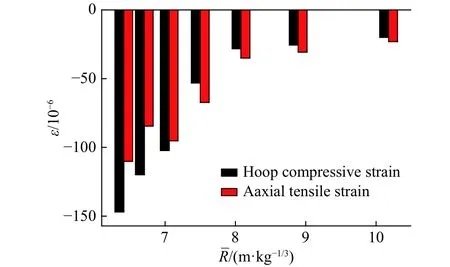
图11 位置3-1环向和轴向最大应变Fig. 11 The maximum hoop and axial strains at position 3-1
4.2 管道和地面振动速度数据和分析
测振仪Y轴方向平行于管道轴线,X轴在水平面内和Y轴垂直,Z轴垂直于地面,地表测振仪布置方向同管道相一致。典型的振动速度时程如图12所示,管道和地表各方向的峰值振动速度(PPV)和主频见表4和表5。从测试结果可以看出,管道上的X轴方向振动大于Y轴方向,大体和Z轴振动水平相当,地表X轴方向振动大于Y轴方向,Z轴方向振动最大,这是由于在地表存在波形转换。
从表4和表5可以看出,总体上地表和管道主频随药量增大而减小。且在本次实验条件下,土体主频衰减较管道衰减快。图13表示地表主频衰减曲线,采用幂函数形式回归,X、Y、Z方向衰减指数分别为-0.447、-0.863、-0.432;决定系数分别为0.724 5、0.867 2、0.918 7。而管道主振频率影响因素众多,除土体因素外,还受管材、截面几何性质和管端约束条件等因素的影响,衰减规律更复杂,采用幂函数形式回归效果不好。地表和管道主频处于同一个量级,两者大体上比较接近,管道主频略高于地表主频。这是由于管土结构耦合振动中,管道的振速主频要受土体主频和管道自身固有频率影响,管道各阶固有频率远比土体主频高,综合的结果是管土耦合作用后主频略高于地表主频。最大合成速度幅值衰减按萨氏公式回归,如图14所示。峰值振速衰减指数大体和管道轴向应变曲线衰减指数相当,地表合成速度的幅值要大于管道合成速度的幅值。有意思的是,在本次实验条件下两者约为2倍的关系,幅值随埋深的衰减规律在后面实验中值得继续研究。

图12 PE管和地表振动速度信号(Q=100 g)Fig. 12 The vibration velocity signals of the PE pipe and ground (Q=100 g)
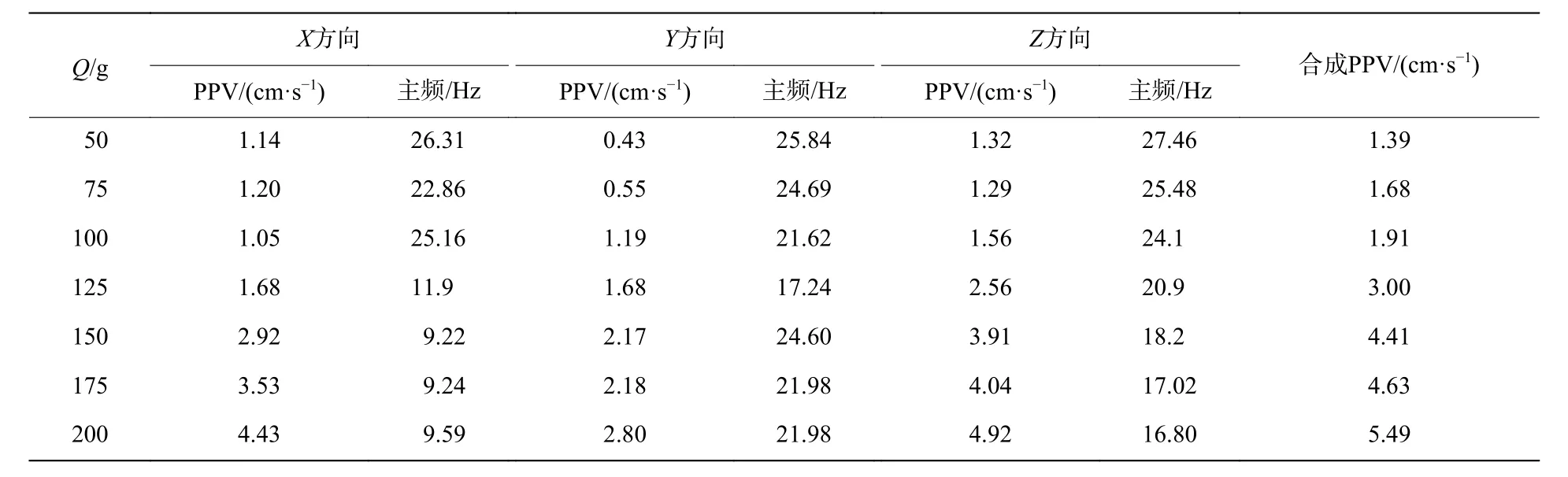
表4 不同药量下PE管的PPV和主频Table 4 The PPVs and main frequencies of the PE pipe under different explosive charges
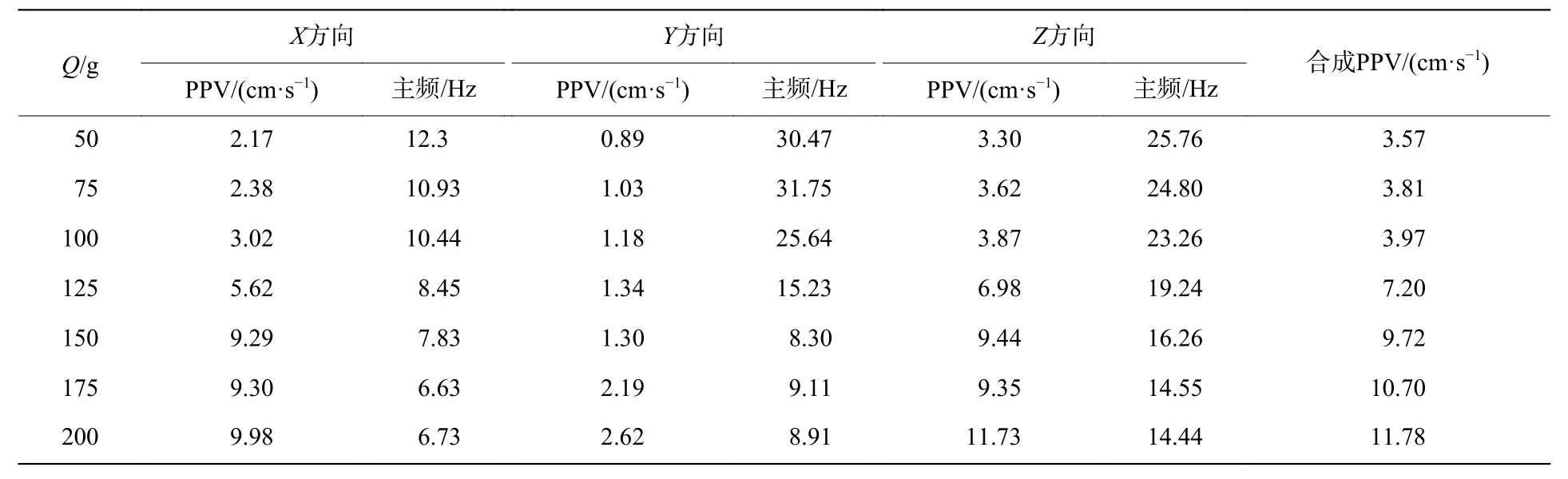
表5 不同药量下地表的PPV和主频Table 5 The PPVs and main frequencies of the ground under different explosive charges
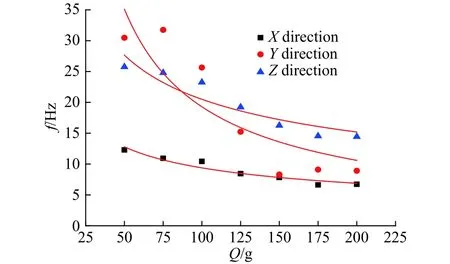
图13 地表主振频率随药量的衰减Fig. 13 Main frequency attenuation of ground vibration with explosive charge
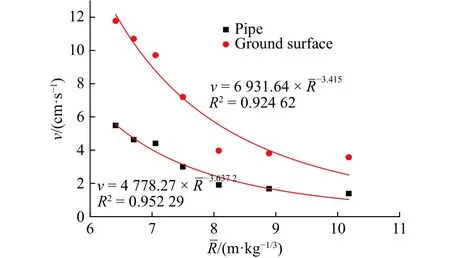
图14 地表和管端合成速度随比例距离的衰减Fig. 14 Resultant velocity attenuation of the pipe and ground with scaled distance
4.3 对比分析
根据2.2节,取cp=1 100 m/s,其他参数同2.1节 PE管参数,地面振动速度数据见表5,代入式(1)~(3)。取不同比例距离的理论计算值和截面3测点3实测数据对比,如表6所示。随着比例距离增大,已有理论公式计算值精度逐渐提高,而在比例距离较小时已有理论公式计算值远较实测值小。考虑到式(1)推导时假设爆炸波为平面波前,式(2)和式(3)是综合了模型和原型实验大量数据拟合而得到的,因此对于爆炸波中远区(本文中建议比例距离),且土体含水率较低时,现有的计算公式具有较好的精度。对于比例距离的情况,且含水率较高时,建议依据土体含水率的不同,应用本文拟合曲线做适当折减修正得到爆炸波引起的附加应变值。
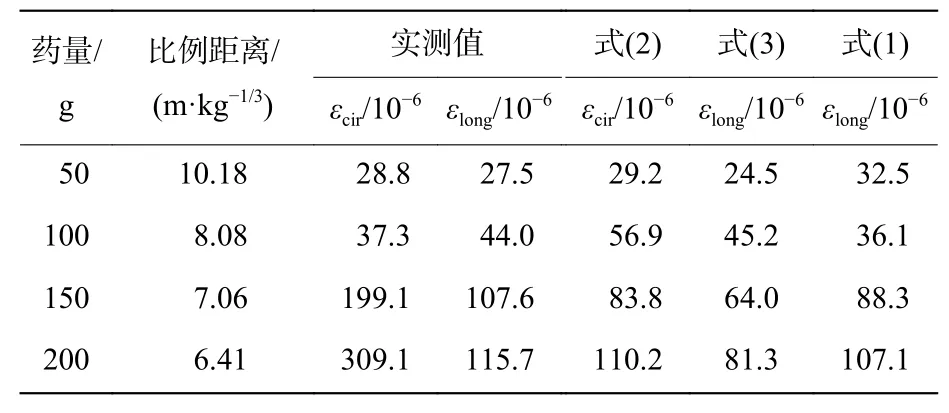
表6 已有公式计算值和实测数据Table 6 Deteced data and calculated values by existing formulas
4.4 管道动压力信号和分析
压电陶瓷片做被动测试时,具有抗干扰能力、对压力信号变化敏感度高等优点,可直接将动态的压力信号直接转换为电压信号,因此检测十分方便。本次实验中6片压电陶瓷片,对称分布在截面6、3、7中心的迎爆和背爆中心线两点上。6片压电陶瓷片在整个实验期间工作稳定,同时具有很强的抗干扰能力,表现出优良的动态性能。压电陶瓷片极化方向的压电常数为d31,在本次实验中测试的是测点轴向压力。图15为药量为75 g时,背爆面测点1的3个动压力时程曲线图,可以看出爆心距最小的截面3测点电压极值明显大于其他2个截面。对动应变时程做时间的一阶数值微分得到动应变的变化率即应变率,对比同位置的压电陶瓷片所测得的时程曲线,两者具有相似性。取药量150 g,截面3测点1轴向应变时间历程曲线如图16所示,数值微分后如图17(a)所示,压电陶瓷片所测得时间历程曲线如图17(b)所示,对两信号做相关分析后结果为强相关,相关系数为0.603 8,对压电陶瓷片去直流处理后做显著性校验,在5%的显著性水平下,同分布假设不被拒绝,可信概率为0.795 0。

图15 典型的压电陶瓷片信号Fig. 15 The typical signal of PZT voltage
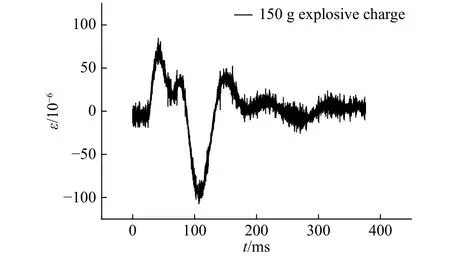
图16 位置3-1轴向应变时程曲线Fig. 16 The time history curve of axial strain at position 3-1
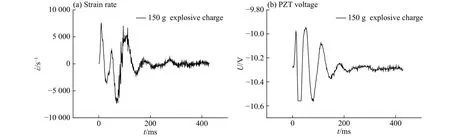
图17 位置3-1轴向应变率和电压时程曲线Fig. 17 The time history curves of PZT voltage and axial strain rate at position 3-1
5 结 论
(1) 在比例距离6~11 m/kg1/3范围内,埋地PE管受爆炸波局部冲击的作用,各点之间应力分布并不均匀,比例距离较小时,各点的环向应变大体上要比轴向应变大,管道原圆截面形状发生改变,局部变形特征明显。随着比例距离的增大,爆炸波由压缩波向地震波做波形转换,各点最大拉应力和最大压应力幅值差逐渐减小,局部变形效应逐渐减弱,整体变形效应相对变大,轴向应变逐渐开始占主导地位[11]。因此在爆炸波作用下近距离管道安全校核时,管道环向应力应该作为主要因素之一考虑。
(2) 通过量纲分析和实验数据分析验证了管道应变和比例距离具有良好的幂函数指数衰减关系,采用综合药量和爆心距2个因素的比例距离作为描述问题的主要变量,将其他如爆源、土体、管道结构等复杂因素的影响简化为比例系数和衰减指数,是一种有效的解决工程实际问题的简化方法,和现有的工程习惯表达一致。从本次实验数据分析可知:在黏性土中爆炸产生和传播的爆炸波速度衰减指数要比一般设计手册中萨氏公式给出的岩土衰减指数要大。
(3) 压电陶瓷片在本次实验中表现出了良好的动态特性,工作稳定、防水处理简单、抗干扰能力强、测试简单可靠,可以直观地反映动态压力的变化。因此将其用做爆破现场监测的技术手段是值得推广的,这方面的研究工作亟待加强。
(4) 应用已有公式计算管道应变时,应注意公式适用条件。由于高饱和黏土中含水量高,有利于爆炸波能量传播,局部冲击下柔性PE管会产生较大的环向应变。

