考虑跃迁的指数型炸药空爆荷载等效静载动力系数*
耿少波,李 洪,葛培杰
(1. 中北大学土木工程学科部,山西 太原 030051;2. 长安大学桥梁结构安全技术国家工程实验室,陕西 西安 710064;3. 大连理工大学水利工程学院,辽宁 大连 116024)
对防护结构及建筑结构而言,炸药空爆荷载具有超压峰值高、作用时间短、扩散速度快等特点,相比其它设计荷载,为典型的动力荷载。在结构设计阶段,若能将此爆炸荷载等效为静载计算,可避免繁琐的非线性有限元分析,易为结构工程师所接受和使用。因此,多数规范中[1-7]爆炸荷载均按考虑动力系数的静载进行结构计算。入射超压从零跃迁至正超压峰值时长占冲击波正超压作用时长比值很低,故规范常省略此跃迁升压阶段,为简化计算,并进一步将入射超压简化为线性衰减荷载。
爆炸荷载等效静载理论研究方面研究较多。Biggs[8]对线性衰减类动力荷载进行等效静载处理,并用于爆炸荷载近似计算。伍俊等[9]采用等效单自由度与有限元方法对防爆墙结构进行对比分析,模型中爆炸荷载为未考虑跃迁升压的线性衰减荷载模式,他指出等效单自由度静载方法结构设计具有良好精度。颜海春等[10]采用爆炸荷载等效静载对人防工程封堵梁内力分析,但未指出结构延性比与荷载动力系数之间的详细关系。杨涛春等[11]采用爆炸荷载线性衰减函数对钢混组合梁进行了等效静载与有限元分析对比计算,但计算未涉及结构自振频率、延性比。Baker等[12]指出空爆冲击波呈指数型衰减,等效冲量计算按此计算较准确。杨科之[13-14]研究了直线衰减荷载作用下动力系数与延性比的关系,延性比较大时动力系数可计算范围受限。陈俊杰[15]研究了爆炸荷载冲量简化分析方法,所采用的荷载形式为线性衰减荷载模式。Chen等[16]采用等效荷载分析了地下拱结构-土体爆炸耦合效应,指出了冲击波等效单自由度的有效及方便性。Shi等[17]指出采用指数型函数进行爆炸荷载冲量及等效静载时会更准确,但未考虑跃迁段的影响。Gantes等[18]计算了指数型爆炸荷载作用单自由度结构的弹塑性位移响应解,但尚未明确与划分荷载作用时间与结构进入塑性阶段时间关系,且未对结构延性比、动力系数分析。Louca等[19]分析爆炸作用时指出正超压衰减段采用指数型函数拟合会更接近冲击波实测结果。
设计延性比与荷载作用时长有关,线性衰减荷载正超压等效作用时长小于爆炸冲击波正超压作用真实时长,这对动力系数影响如何?同时,忽略升压过程对结构的动响应尤其对结构弹性响应,继而对结构塑性阶段响应及延性比、动力系数的影响程度如何,国内外学者鲜有研究。
因此,本文考虑超压从零跃迁升压至超压峰值,以指数形式从超压峰值衰减至零的分段荷载函数进行等效单自由度体系下结构弹塑性动力系数分析,并与设计规范中采用的未考虑升压阶段的等冲量线性衰减荷载动力系数计算结果对比,为基于延性比的抗爆结构设计提供理论支持。参考笔者前期所做的TNT、B炸药空爆冲击波衰减波形测试工作及已出版文献[20],常规炸药等化学爆炸跃迁升压至超压峰值时长所占正超压作用时长比一般为3%以下,且接近直线升压,因此本文考虑的升压为直线跃迁升压模式。
1 理想弹塑性体系动力微分方程
1.1 等效单自由度微分方程
常规炸药等化学空爆冲击波正超压作用时长很小,小于结构出现最大动位移反应时间[5]。根据结构动力学等效单自由度理论及达朗贝尔原理,其等效单自由度体系弹性阶段微分方程:

式中:kM-L为弹性等效质量-等效荷载系数比,m为结构单位长度质量,W(t)为结构动位移,l为结构长度,K为结构等效弹簧刚度,Δp(t)为爆炸荷载时程函数。
设在tT时刻,结构弹性位移达到最大值WT,速度为vT,之后结构进入塑性振动。结构塑性阶段微分方程为:

式中:km-l为塑性等效质量-等效荷载系数比,qm为结构塑性阶段结构抗力。

图1 荷载简化及作用时长Fig. 1 Schematic diagram of load types and load durations
图1给出了3种荷载模式的时程曲线。作为等效时长计算对比的基准量,不考虑跃迁段的指数型衰减荷载所对应的函数为:

式中:Δpm为超压峰值,f(t)为荷载归一化函数,t+为冲击波正超压作用时长,a为荷载曲线形状调整参数。
作为动力系数对比的基准量,不考虑正超压跃迁段,采用等冲量线性衰减荷载模式时,对应的函数为:

式中:tI为等冲量线性衰减荷载等效作用时长。
增加跃迁时间而不改变正超压作用时长的指数型衰减荷载模式,对应函数为:

式中:t0为荷载从0跃迁至超压峰值跃迁时长。
由式(1)及杜哈梅积分可知,在弹性阶段:

式中:Wcm为超压峰值为静载数值时对应的结构位移,ω为振动角频率。
在tT时刻弹性响应结束准备进入塑性响应,此时对应结构最大弹性位移及速度:

且可知塑性阶段结构任一时刻t对应的结构速度及位移为

由于结构动荷载等效为基于理想弹塑阶段内的等效静载,其动力系数表达式为

1.2 冲量及等效时长分析
由冲量定义及图1所示,未考虑跃迁的指数型衰减荷载所对应冲量函数表达式

荷载曲线形状调整参数a数值越大,指数型衰减荷载所对应的曲线越陡峭,负超压峰值及作用时长越小。为较好拟合测试曲线,其数值取值范围可取1.27≤a≤1.61[11],为满足建筑结构抗爆设计一般特点,本文取端部值即1.27与1.61为后续分析参数值。
结合图1荷载曲线所包围的面积变化可知:t0时刻之前,考虑跃迁后的指数型衰减荷载所对应的冲量数值小于未考虑跃迁的指数型衰减荷载冲量数值,t0时刻之后该冲量又偏大。因此需计算其冲量:

将式(13)~(14)做函数差值对a进行求导分析,可知对于任意的t0>0,当a>0时,公式(14)对应的数值为大,即考虑跃迁后,冲量随之增大,对结构抗爆设计偏不利。
以式(13)为基准,未考虑跃迁的等冲量线性衰减荷载,其等效时长为:

即指数型衰减荷载真实作用时长t+与等冲量线性衰减荷载等效时长ti的比值δ分别为1.464、1.6。
2 结构体系塑性阶段划分
常规炸药空爆冲击波作用时长t+很短,经等冲量换算后的线性衰减荷载等效时长tI更短,结构完成弹塑性最大变形时间tm>t+及tm>tI,即此时对应结构外荷载为零。结构完成弹性变形进入塑性变形时刻tT存在两种可能性:t0<t+<tT<tm,即较晚进入塑性阶段及t0<tT<t+<tm,即较早进入塑性阶段。
为精简篇幅,本文只给出考虑跃迁的指数型衰减荷载动力系数求解过程及公式,等冲量线性衰减荷载求法简单,公式不再单独求解,而以其计算结果的相对差值比例在本文工况示例计算给出。
2.1 较晚进入塑性阶段
若令 θ0=ωt0,θT=ωtT,θ+=ωt+,由公式 (7)计算考虑跃迁的指数型衰减荷载等效静载动力系数:

若定义A=Kh

因θT为中间变量,所以需将其求出,求解后其表达式为

由式(8)可得考虑跃迁的指数型衰减荷载弹性阶段结束时对应的振动速度与位移比值为

由式(9)及塑性阶段v(tm)=0可导出

由式(10)及塑性阶段v(tm)=0可导出

由式(11)可知

式中,Wm为结构进入塑性阶段结构最大位移。又因为

将式(20)、(22)代入式(21)后可知

2.2 较早进入塑性阶段
若令θm=ωtm,由前述定义t0<tT<t+<tm及动力系数公式可知,考虑跃迁的指数型衰减荷载等效静载动力系数为:

由式(7)可得考虑跃迁的指数型衰减荷载对应的弹性结束时对应的振动速度为

由式(10)及塑性阶段v(tm)=0可得速度的另一解为

代入式(11)后可得

3 弹塑性阶段动力系数计算算例
3.1 工况分组及计算结果
根据跃迁时长占正超压总时长的比值(t0/t+)、爆炸荷载正超压作用时间t+与等冲量线性衰减荷载等效时间tI比值δ确定了4种典型计算工况。为相互对比,以等冲量线性衰减荷载结构荷载参数θI=ωtI为0.2~2.8,0.2为步长,共计14项作为基本计算数据,而ωt+(即θ+)按作用时长与等效时长换算后再计算为对比数据。为能涵盖工程结构设计时所对应的延性比,延性比β为1~5作为计算范围。工况分组如表1所示。
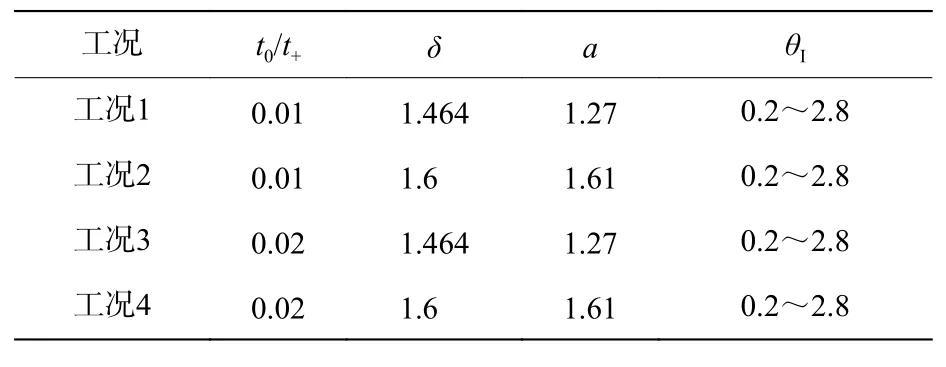
表1 工况分组Table 1 Calculation cases
由式(23)及(28)可知,动力系数Kh不为显式函数,由θT、θ+、θm定义及延性比β的范围作为控制条件,分别赋初值后迭代求解并汇总。工况1计算结果及与线性衰减荷载的差异比值见表2。 表中β为1.0数据列为结构动力系数公式退化至弹性状态时求解结果,红色间断线左侧数据为考虑跃迁升压的指数型衰减荷载模式下结构较晚进入塑性阶段所对应的公式计算得出,红色间断线包围的右侧数据为考虑跃迁升压的指数型衰减荷载模式下结构较早进入塑性阶段所对应公式计算得出。表中蓝线左上方(右下方)数据为等冲量线性衰减荷载模式下结构较晚进入塑性阶(较早进入塑性阶段)段所对应计算公式得出。工况1~工况4之间相对差值及与直线型衰减荷载差异如图2所示。

表2 工况1动力系数计算KhTable 2 Dynamical coefficient Kh for calculation case 1

图2 线性衰减荷载与本文荷载计算模式动力系数对比Fig. 2 Dynamical coefficients comparison between linear load and exponential loading with transition
由表1、图2、各计算工况与规范指定的等冲量线性衰减荷载计算结果可知,延性比β<1.6时,等冲量线性衰减荷载动力系数偏大;β>1.6时,线性衰减荷载计算数值先偏大后偏小。线性衰减荷载的ωt+对应的设计范围明显偏小;β≤3.0时,考虑跃迁的指数衰减荷载计算结果数值大小依次递减顺序为工况3、1、4、2,其中工况3与工况1之间的差异最大值为1.2%,最小为0,平均为0.4%,差异极小;工况4与工况2之间的差异最大值为1.5%,最小为0,平均为0.7%,差异很小,略大于工况3与工况1之间的差异,即跃迁时长比对动力系数的影响很小,β=5.0时,跃迁时长比对动力系数的影响可忽略,指数形状调整参数影响效果明显。
结合图2,以工况1与工况2之差异为典型对比,取规范采用的等冲量线性衰减荷载为基准量,分析指数形状调整参数a对动力系数的计算结果影响(η),见图3所示。
设计参数θ+<0.8δ时,工况1和工况2之间的差异逐渐增大,数值上仍很小,差异数值最大为2%,0.8δ<θ+<1.4δ时,除β=5的差异约为5.0%以外,其它延性比对应的工况1和工况2之间的差异先减小后增加,数值上仍很小,差异约仍小于2%;1.4δ<θ+<2.2δ时,工况1和工况2之间的差异逐渐增大,趋于稳定数值,平均约为3.8%,说明形状调整参数a对计算结果的影响与设计参数θ+紧密相关。

图3 线性衰减荷载与典型工况结果差异性比值Fig. 3 The difference ratio between linear decay load and typical calculation conditions
3.2 结果分析
考虑跃迁升压的指数型衰减荷载等效静载动力系数,其求解结果可分为弹性状态、较晚进入塑性状态、较早进入塑性状态3种类型,3种物理含义对应的间数据能很好衔接;等冲量线性衰减荷载等效静载动力系数也有此3种状态,但当θ+>1.4δ时,弹性状态数据直接与较早进入塑性状态的数据进行衔接,缺少较晚进入塑性状态的过渡。在同一爆炸荷载作用下,若结构设计的柔度越大,即θ+数值越小,对应的等效静载动力系数越小,在θ+<0.4δ时,4种工况对应的动力系数均大于由等冲量线性衰减荷载计算数值,最大数值为1.7%,误差较小;当0.6δ≤θ+≤1.2δ时,其动力系数均小于等冲量线性衰减荷载计算结果,最大误差为10%,当θ+>2.2δ时,或当设计延性比β=5且θ+>1.4δ时,等冲量线性衰减荷载动力系数无解而考虑跃迁的指数型衰减荷载有解。
特别地,4种典型工况中,均当延性比β=3且θ+>1.4δ时,考虑跃迁后的指数型衰减荷载等效静载动力系数均大于等冲量线性衰减荷载等效静载动力系数数值,且大于幅度较高,最大误差为17.7%,即此区间按规范所规定的等冲量线性衰减荷载进行等效静载设计时,偏不安全。
相同跃迁时长比值下,当θ+<0.4δ时,即柔度特别大的结构,形状调整参数a对应的动力系数计算数值误差基本为0,即形状调整参数a在此范围对计算结果不敏感;较晚进入塑性状态范围内,随着形状调整参数a的提高,动力系数计算数值变小;较早进入塑性状态数据,随形状调整参数a的提高,动力系数计算数值增大。
相同的指数荷载形状调整参数a下,随着跃迁时长比值的增加,所有工况的动力系数均增加,增加幅度较小且有限,最大值1.5%,即不考虑跃迁会导致计算结果偏小,但误差可忽略。
4 结 论
以考虑升压跃迁的指数型衰减荷载为研究对象,考查了与等冲量线性衰减荷载等效静载动力系数的差别,并分析了跃迁时长比、指数形状调整参数对动力系数的影响,得到以下主要结论:
(1) 与等冲量线性衰减荷载相比,考虑跃迁的指数型衰减荷载动力系数弹性状态、较晚及较早进入塑性状态衔接更为合理,可进行设计的延性比β与结构荷载参数θ+范围更广,较小β及结构荷载参数θ+对应的动力系数较小,对应为当前现行结构设计规范设计偏安全;较大β及θ+对应的动力系数偏大,且幅值较高,若此范围区间仍采用规范类线性衰减荷载进行抗爆设计,偏不安全;
(2) 相同跃迁时长比值下,指数荷载形状调整参数a越大,对较早进入塑性状态动力系数提高越大,对θ+<0.4δ对应的较晚进入塑性状态计算结果基本不产生影响,对θ+>2.5对应的较晚进入塑性状态计算数值为降低作用;
(3) 相同指数荷载形状调整参数a下,跃迁时长比值增加会导致动力系数结果提高,但幅度有限,最大值1.5%,平均值依据不同工况在0.4%~0.7%范围,可忽略其影响。

