采用改进鲸鱼算法的配电网综合优化
孙 琪,于永进,王玉彬,高海淑
(1.山东科技大学电气与自动化工程学院,青岛 266590;2.国网技术学院,济南 250002)
随着传统化石能源的枯竭及环境保护的需要,大量分布式电源DG(distributed generation)和电动汽车EV(electric vehicle)接入配电网。DG与EV的普及在节约能源、保护环境等方面有明显优势。但是由于DG与EV负荷具有随机性,可能会改变系统潮流,扩大负荷峰谷差,对电能质量及电力系统稳定造成巨大影响[1-3]。因此,忽略DG与EV的影响而采用原来的控制策略必然会使配电网不能运行在最优状态,造成损耗加剧、电压越限和功率分布不均等问题,因此考虑它们的特点进行配电网优化具有重要意义。
配电网重构与无功优化都是重要的优化手段。重构可以通过控制分段开关、联络开关状态来改变配电网络拓扑结构,起到减少网损、改善节点电压与平衡系统负荷等效果。无功优化最常见的方式为并联电容器组就地进行补偿,可以改变线路无功分布,减少网络损耗,抬升电压。本文采用静电电容器与晶闸管开关电容器型静止补偿器作为无功补偿设备。
近年来,许多学者对含DG配电网重构、配电网无功优化、EV接入电网等问题展开了研究[4-10]。文献[5]提出了3条编码规则,采用改进萤火虫算法进行求解,提高了计算效率,但是仅仅考虑了静态重构问题;文献[6]在配电网无功优化问题中加入DG,利用传统鲸鱼算法进行求解,降低了网络损耗,然而其并没有结合配电网重构使优化结果更好;文献[7]在配电网重构问题中加入了EV和DG,建立了多目标重构模型,但没有对配电网进行无功优化;文献[8]针对配电网大规模非线性混合整数规划的特点,将粒子群算法引入和声搜索HS(harmony search)算法,提高了算法的搜索能力,但算法编程复杂,运算速度慢;文献[9]在粒子群优化PSO(parti⁃cle swarm optimization)算法中结合了遗传算法杂交环节与模拟退火算法的Metropolis更新机制来增强算法搜索能力,但计算时间较长,并且没有考虑动态重构问题。
综上所述,针对目前含EV与DG的配电网综合优化研究中存在的没有综合考虑优化和算法性能不佳等问题,本文将无功补偿容量与网络开关状态同时作为控制对象进行动态综合优化。以网络损耗、电压改善度、负荷均衡度及开关动作次数为目标构建数学模型,在算法方面利用Sobol序列生成分布更均匀的初始鲸群,可以更好地遍布搜索空间。针对传统鲸鱼算法缺少全局交流问题引入自适应权重调整系数,使算法均衡全局搜索与局部勘探能力,更容易跳出局部最优,改进了传统的越界拉回机制,增加样本多样性的同时产生精英粒子,提高算法寻优效率。考虑日负荷、DG出力与EV充电负荷的变化,采用信息熵时段划分法进行日负荷分时段动态优化,减少了开关动作次数。
1 配电网综合优化数学模型
1.1 目标函数
(1)网络损耗最小的目标函数为

式中:i为支路编号;n为网络中包含支路总数;ki为支路i的开断状态;Ri为支路i阻抗;Pi、Qi分别为流过支路i的有功、无功功率;Ui为支路i末端节点电压;f1为最小网络损耗。
(2)电压改善度最大的目标函数为

式中:j为节点编号;N为节点总数;Uj为节点 j的实际电压,也就是迭代过程中在每一种重构策略对应下的节点电压;Ujs为节点 j重构之前电压;f2表示相比于重构前,在当前重构策略下节点电压的最大改善度。
(3)负荷均衡度最小的目标函数为

式中:m为网络中闭合支路总数;Si、Simax分别为第i条支路复功率实际值与上限;负荷均衡度较小表示负荷分布更均衡;f3为最小系统负荷均衡度。
(4)最小开关动作次数的目标函数为

式中:K为开关动作次数;M为开关数量;xkt0和xkt分别为开关k在t时段重构前、后的状态;f4为最小开关动作次数。
(5)目标函数归一化。将多目标优化问题进行归一化可以简化编程,提高寻优效率,得到兼顾各目标函数的最优解。适应度函数表示为

式中:f为适应度函数;ωβ(β=1,2,3,4)为各目标函数权重系数,代表了各分目标函数在适应度函数中的重要程度;F1、F3分别为目标函数1、3每次迭代的最小值;F2为目标函数2每次迭代最大值;F4max和F4min为目标函数4每次迭代的最大值与最小值;本文各目标权重依次为0.50、0.25、0.15、0.10。由于f2为最大值形式的目标函数,为使适应度函数合理化此处取 f2的负值加入到适应度函数中。
1.2 约束条件
(1)满足功率平衡的约束条件为
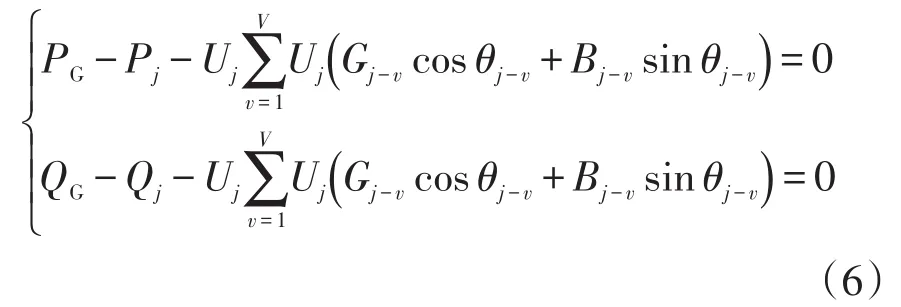
式中:PG、QG分别为DG注入节点的有功、无功功率;Pj、Qj分别为节点j负荷的有功、无功功率;Uj和Uv分别为节点j和v电压;节点v与节点j相连;V为节点j相连的节点总数;θj-v为节点j和节点v之间的电压相角差;Gj-v和Bj-v分别为节点导纳矩阵的实部和虚部。
(2)满足系统运行的约束条件为

式中:Umax、Umin分别为节点j的电压上、下限;Imax、Imin分别为流经支路i的电流上、下限;PG、PGmax为DG的实际出力与出力上限;Qj和Qjmax分别为节点j的无功补偿装置的出力和出力上限。
1.3 DG数学模型
DG可以看作是一组连续实数变量,对其最简单的处理就是看作“负”的负荷。对于有功功率确定且功率因数维持稳定的异步发电机型分布式电源可处理为PQ节点,处理方法为

式中:PG、QG为DG发出的有功、无功功率;P和Q为DG对节点负荷的影响值,并将与原节点功率叠加。
2.4 等效负荷信息熵分段
各时段等效负荷概率为

式中:we为第e个时段负荷;Δte为时段e持续时长;E为分段数,未分段前取24。
E分段下的负荷曲线信息熵为

未分段时信息熵没有损失,随着分段数逐渐减少,信息熵损耗变大,如图1所示。首先选取任意相邻时段进行合并,取负荷均值进行信息熵计算,取具有最小信息熵的合并方式作为此时E-1分段情况下的信息熵值HE-1,重复进行此步骤直至分段数降为1。HE为关于分段数k的凸函数,起点与终点做直线L,HE各点向直线作垂线,其中距离最大的H0所对应的E值即为最优分段数[11]。

图1 负荷曲线熵函数Fig.1 Entropy function of load curve
2 改进鲸鱼算法
2.1 标准鲸鱼算法
鲸鱼算法[12]是通过模仿座头鲸气泡网狩猎策略提出的,气泡网狩猎策略包括搜索猎物的全局勘探,包围、接近猎物的局部开发。鲸鱼算法具有操作简单、控制变量少、搜索能力强等特点,一些学者已经对其开展了研究[13-14]。鲸鱼算法可以用于解决配电网优化问题,本文将每条鲸鱼个体看作每种优化策略,将鲸鱼位置的维数对应配电网优化问题的维数,这样在鲸鱼不断更新自身位置的过程中可以求得最佳优化方案。其基本寻优原理如下。
1)收缩包围猎物
当座头鲸发现猎物后,若随机概率P(P为[0,1]的随机数)小于0.5,那么就逐渐靠近猎物,其公式为

式中:X(t+1)为更新后的位置;X(t)为当前个体空间位置;X*(t)为第t次迭代中的最优鲸鱼位置;D为最优解与当前个体差距;A、C为系数变量;r1、r2为[0,1]的随机数;a为迭代过程中从2下降到0的线性递减向量;max_iter为最大迭代次数。
2)螺旋更新位置
当座头鲸发现猎物后,若随机概率P不小于0.5,那么就进行螺旋方式靠进猎物,其公式为

式中:D′为鲸鱼到当前最优解的距离;b为螺旋形状常数;l为[-1,1]内的随机数。
3)随机搜索猎物
为提高全局搜索能力,鲸鱼个体也可以随机搜索猎物。当随机概率P不小于0.5时,若A超出[-1,1]范围,距离数据D随机更新。此时鲸鱼个体会放弃原本的目标,向其他方向随机搜索新猎物,使算法提高全局搜索性能,防止陷入局部最优,位置更新方式为

式中,Xrand为随机选择的鲸鱼的所在位置。
2.2 鲸鱼算法的改进
本文对传统鲸鱼算法做出以下3点改进。
1)基于Sobol序列的种群初始化
文献[15]指出,对于解分布未知的问题,个体的初始值应尽可能地均匀分布在数据空间中,使种群保持较高的多样性。传统WOA算法采用随机数形式产生初始鲸群,不能使初始鲸鱼个体均匀分布在解空间。由于随机分布的原因可能使最优解附近种群分布稀疏,进而影响计算效率,种群的过度聚集也会造成局部最优情况,这都影响配电网最优控制策略的产生。采用Sobol序列可以产生超均匀分布粒子,可以改善初始鲸群多样性。图2和图3分别为用Sobol序列与随机数方式在[0,1]范围内生成500个粒子对比情况。

图2 随机数生成分布Fig.2 Distribution of random number generation

图3 Sobol序列分布Fig.3 Distribution of Sobol sequence
Sobol序列生成初始鲸群方法为

式中:xmax、xmin为分别为鲸鱼位置上、下限;λ为Sobol序列生成的位于[0,1]范围内的随机数;x1为第1头鲸鱼位置,其他鲸鱼位置以此类推。
2)自适应调整权重系数
惯性权值是智能算法中的一个重要参数[16],在本文中表示算法对全局与局部搜索能力的侧重力度。本文采取权重递减的方式来提高WOA算法性能,权重系数设置为

式中:ωmax、ωmin分别为权重系数上、下限,本文分别取为1.5和0.5;t为当前迭代次数。
将权重系数加入到式(11)和式(16)中,得

3)越界处理机制
目前鲸鱼算法对越界鲸鱼常见的处理为舍弃或拉回边界处,如此处理前者会降低样本多样性,后者会使边界处聚集大量粒子,不利于算法收敛。本文结合精英策略提出更新越界鲸鱼的位置使其更靠近当前最优鲸鱼的策略,既保留了鲸群样本多样性,又使位置更新后的鲸鱼具有较好的适应度值,同时增加了当前最优控制策略附近的解的个数,更容易得到最优解。
当鲸鱼a的位置xa≥xmax或xa≤xmin时,越界鲸鱼更新位置为

式中:d为当前搜索空间中适应度最好的粒子与距离它最近的粒子之间的欧氏距离;h为鲸鱼位置更新距离矩阵,维度与鲸鱼相同;hg为矩阵h的第g维矩阵。
改进后的算法流程如图4所示。

图4 改进WOA算法流程Fig.4 Flow chart of improved WOA algorithm
3 算例分析
3.1 基本参数
本文对IEEE33节点系统进行仿真验证。现初始参数设置如下。①网络初始参数:该配电系统含节点33个,支路37条,联络开关5个,总负荷为3 715+j2 300 kV∙A。其他详细网络参数可参照文献[17]。②算法初始参数:种群数量为60,最大迭代次数为80。③DG的接入位置与容量如表1所示。④在节点8、16、30处设置无功补偿装置,最大无功补偿容量为200 kvar。⑤在节点23、32处设EV充电站,各投入25辆EV,每辆EV电池总容量大小为33.8 kW∙h,充电功率为5 kW,所有电动汽车均在此处充电。配电网络结构如图5所示。

表1 DG接入位置及容量Tab.1 Access locations and capacities of DGs

图5 配电网结构Fig.5 Structure of distribution network
3.2 静态优化分析
为验证改进WOA算法的性能,在不考虑DG与无功优化的情况下进行静态重构,重构结果与文献[18,9]的对比如表2所示。

表2 文献重构结果对比Tab.2 Comparison among reconstruction results in the literature
由表2可以看出,各文献重构后结果相对于重构前都有明显改善,此场景为简单情况,本文算法断开开关组与对比文献相同,采用前推回代法计算网络潮流,网损较重构前下降31.17%,验证了本文算法有效性。
为比较算法对本问题的优化效果,利用本文算法、改进粒子群算法[9,19]以及改进和声算法[18,20]对同一网络进行优化,结果对比如图6和表3所示。

图6 迭代收敛曲线Fig.6 Iterative convergence curves

表3 算法重构结果对比Tab.3 Comparison among reconstruction results obtained using different algorithms
由图6及表3可以看出,3种智能算法在迭代精度方面相近,本文算法寻优精度较好。在寻优效率方面,其他两种算法收敛次数分别为25次和15次,本文所提算法平均迭代次数为10次,迭代次数最少。上述3种智能算法各运行20次后,本文算法平均耗时明显少于其他两种算法,寻优效率较高。由图6选取的迭代曲线可以看出,本文算法采用的So⁃bol序列法生成的初始种群靠近最优解的概率较大,初代粒子中最优网损较低,事实上在20次运算中本文算法的初代粒子中最优网损值平均为178.5 kW,而另外两种算法的初代最优网损为188.6 kW。
为测试综合优化效果,在不考虑DG与EV情况下分4个场景进行优化,结果如表4和图7所示。

图7 各节点电压Fig.7 Voltage at each node

表4 优化结果对比Tab.4 Comparison among optimization results
由表4可以看出,单独进行配电网重构与无功优化时网损值较优化前分别下降31.17%与24.98%,电压改善度分别为0.600与0.316,负荷均衡度也有所改善。低压配电网一般要求电压偏差小于7%,由图7可以看出:场景1与场景3电压并不满足要求,存在电压越限情况;相比于只进行重构或无功优化,同时考虑两者作用进行综合优化效果更好;由场景4可以看出,综合优化后网损为110.11 kW,较优化前减少45.67%,低于只进行重构或无功优化的情况,电压改善度为0.845,最低电压变化小于7%,符合电压偏差要求,负荷均衡方面也有所改善。
表4中场景3与场景4无功优化结果相同的原因是本仿真为在系统取额定负荷且不含DG的情况下进行的,无功需求大,所以出现全部投入的情况,在后续考虑DG与负荷变化的动态重构分析中无功补偿容量的选择性将被体现。
3.3 动态优化分析
现实生活中负荷、DG出力值与EV充电负荷都是连续变化的量。本文考虑它们的变化性,进行动态重构。考虑EV负荷不确定性,利用蒙特卡罗法模拟EV一天中的有序充电情况[21]。结合某地区风光预测出力值,各时段离散值如图8所示。

图8 EV有序充电负荷变化Fig.8 Changes in orderly charging load of EV
考虑日负荷的变化性,各节点负荷种类、占比、出力大小[22],一天内负荷变化如图9所示。
综合图8和图9建立等效日负荷曲线,并根据文献[11]采用信息熵时段划分法确定最优时段划分来进行动态重构。分段情况如图10所示。
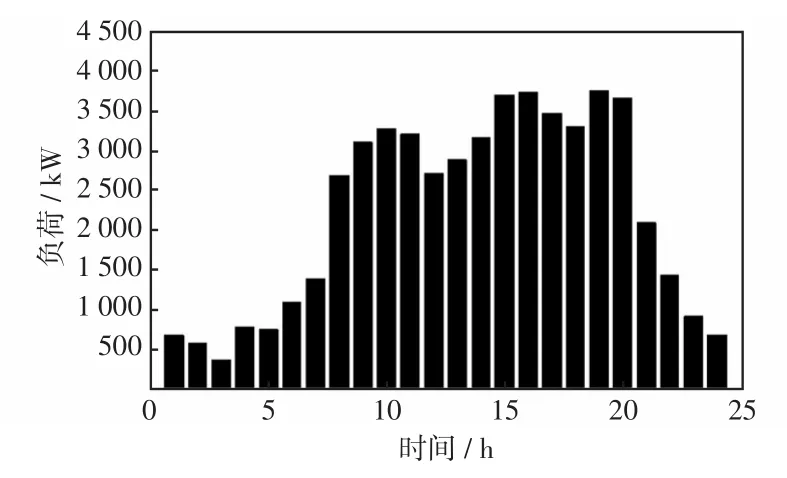
图9 日负荷出力情况Fig.9 Variation in daily load

图10 等效日负荷分段Fig.10 Equivalent daily load segmentation
若在配电网优化过程中略DG、EV与负荷的变化性,采用它们额定值时的优化策略(打开开关组合:7-8/14-15/9-10/25-29/32-33,无功补偿装置出力:150 kvar/200 kvar/200 kvar)时,一天内各时段网络损耗情况如图11所示。

图11 忽略变化性优化策略下日网络损耗Fig.11 Daily network loss under the optimization strategy of ignoring variability
采用图10负荷分段策略进行动态优化,结果如表5所示,将其与不分段动态优化与分段并采用改进PSO算法优化结果进行对比,结果如表6所示。

表5 负荷分段重构结果Tab.5 Load segmentation reconstruction results

表6 重构结果对比Tab.6 Comparison among reconstruction results
由图11可以得出,如果不考虑DG、EV与负荷变化性制定的优化策略在一天内的网络损耗为1 578.93 kW,远高于本文分段动态优化网络损耗,由此可见考虑DG、EV与负荷的变化制定优化策略是有必要的。由表6中的3种优化方式结果可以看出,将等效日负荷曲线分段后再进行综合优化,相比于每时段频繁改变优化策略,在总网络损耗方面虽略有提高,但大大减少了开关动作次数,证明了本文优化策略及改进算法的有效性
4 结语
本文综合考虑配电网重构与无功优化,将线路开关状态、无功补偿容量同时作为控制变量对配电网进行综合优化。建立以网络损耗、电压改善度、负荷均衡度和开关动作次数为目标的配电网综合优化模型。针对传统鲸鱼算法的不足,结合本文问题,在初始种群生成、自适应权重调整和越界处理机制三方面进行改进,提高了算法跳出局部最优能力与寻优效率。通过静态优化结果分析得出本文算法及综合优化策略具有优越性。最后,考虑负荷、DG出力与EV负荷的波动性,采用信息熵时段划分法进行日负荷分时段动态优化,减少了开关动作次数,可以延长开关寿命,减小运行成本。
在今后的工作中将重点考虑高渗透率DG对配电网运行的影响,在优化过程中考虑配电网平均供电可用率和系统供电不足指标等可靠性因素。

