基于离散模型的柔性直流电网短路电流计算方法

辛业春，王 拓，李国庆，江守其，王威儒

（东北电力大学电气工程学院，吉林 132012）

随着可再生能源的持续发展及现有电网技术升级等方面的需求，柔性直流电网拥有非常广阔的应用前景[1]。目前，模块化多电平换流器MMC（modu⁃lar multilevel converter）因其具有的优点成为国内外柔性直流输电工程应用的主流发展方向[2]。然而，基于MMC的柔性直流电网面临一些需要解决的关键技术[3]，如直流故障的快速检测与隔离技术、直流电网潮流控制技术等。基于MMC的直流电网故障隔离技术，存在2条技术路线：①采用具有故障自清除能力的子模块[4]或故障转移型换流器[5]；②采用直流断路器[6]。为了系统的设备选型和保护整定，需要准确计算柔性直流电网故障后的短路电流。

国内外研究机构和学者在直流电网故障分量计算方法方面开展了大量研究。文献[7]分析了MMC直流双极短路故障机制，建立了换流器闭锁前和闭锁后单相等值电路，推导了故障电流应力解析方程；文献[8]研究了双极MMC直流短路的故障特性，建立了换流器闭锁前和闭锁后三相等值电路，推导了故障电流的解析计算公式；文献[9]对比分析了单极和双极柔性直流系统直流短路的故障机理，推导了2种拓扑结构的故障电流解析计算公式；文献[10]分析了MMC直流侧短路故障时交流系统对直流线路故障电流的影响。文献[7-10]分别研究了双端柔性直流系统短路电流计算问题。随着柔性直流电网的发展，直流电网的短路电流计算变得更加重要。文献[11]分析了四端直流电网的直流短路故障特性，推导了不计及远端换流站作用的柔性直流电网故障电流解析计算公式；文献[12-13]分别针对多端单极柔性直流电网单极接地短路故障和极间短路故障，提出了基于状态方程的短路电流计算方法；文献[14]针对多端双极柔性直流电网直流短路故障，提出了基于状态方程的短路电流计算方法；文献[15]分析了直流电网的故障特性，提出稳态分量和故障分量叠加的短路电流计算方法。目前，直流电网故障分量计算方法主要集中在建立微分方程组或复频域方程的暂态电路模型上，随着柔性直流网络规模扩大，微分方程组的降阶求解或复频域转换将变得困难。

针对直流网络故障电气分量数值求解计算的难题，本文在直流短路故障等效电路分析的基础上，提出基于后退欧拉法和梯形积分法的换流器元件及换流站的离散化模型，设计直流电网不同类型故障电流迭代数值求解算法。基于RT-lab平台搭建了四端柔性直流电网仿真模型，对比验证了基于所提模型和故障电流数值求解算法能够准确获得故障电流，适用于大规模柔性直流电网故障电流计算。

1 MMC直流短路故障等效电路建模

1.1 MMC换流器基本结构及工作原理

MMC换流器的基本拓扑结构如图1所示，由3个相单元组成，每一个相单元包含上、下两个桥臂，每个桥臂由N个级联的子模块SM（sub-module）和一个电感L0构成。SM由2个反并联二极管的绝缘栅双极晶体管IGBT（insulated gate bipolar transis⁃tor）和一个电容C0构成。

图1 MMC三相结构拓扑Fig.1 Three-phase topology of MMC

正常工作时，MMC通过控制子模块IGBT的导通和关断，使子模块处于投入或切除状态，维持直流侧和交流侧电压；采用调制和均压控制策略保证子模块电容电压平衡。通过控制子模块投切产生期望的三相交流电压，实现交直流侧功率交换。

1.2 MMC故障等效电路模型

MMC发生双极短路故障且子模块未闭锁时，直流线路注入的短路电流主要包括两部分：一是子模块电容放电电流，二是交流系统馈入的短路电流。由于在较短的时间内，交流系统馈入的电流极小，基本可以忽略[10]，因此MMC直流侧故障电流主要由子模块电容放电电流决定，闭锁前子模块电容放电通路如图2所示。在均压控制的作用下，子模块投切状态不断发生变化，所有子模块的电容均会通过故障点不断放电。

图2 闭锁前子模块电容放电通路Fig.2 SM capacitor discharging circuit before blocking

为描述子模块中开关器件（即IGBT和二极管）的关断和导通状态，将其建模成高、低阻值切换的可变电阻[16]。当开关器件处于导通状态时，其导通电阻为Ron，本文取值为0.01 Ω；当开关器件处于关断状态时，其关断电阻为Roff，本文假设其处于理想关断状态，即其电阻值为无穷大。根据图2所示闭锁前子模块电容放电通路，闭锁前MMC可以等效为RLC串联电路[7，13]，其等效模型如图3所示。

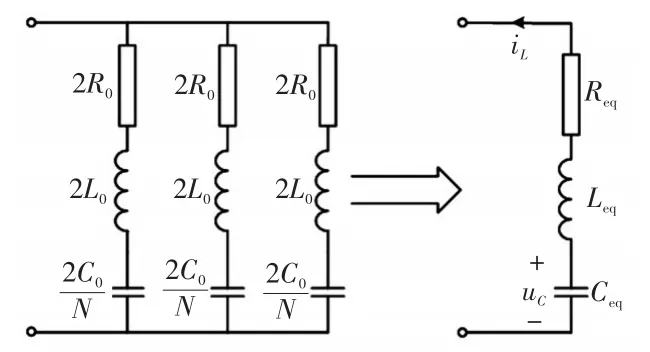
图3 闭锁前MMC等效电路模型Fig.3 Equivalent circuit model of MMC before blocking

闭锁前，MMC的等效电阻Req、等效电感Leq和等效电容Ceq及等效电路初始条件分别为

式中：N为MMC每个桥臂的子模块个数；R0为每个桥臂的等值电阻；L0为桥臂电抗；C0为子模块电容；Udc为换流站稳态直流电压；I0为流经换流站稳态直流电流。

2 柔性直流电网离散建模

2.1 电感和电容离散模型

在MMC闭锁前故障等效电路模型的基础上，可以构建柔性直流电网等效电路模型。结合等效电路元件初始条件，可以建立基于微分方程组或复频域方程的暂态电路模型。随着柔性直流网络规模扩大，微分方程组的降阶求解或复频域转换将变得困难。采用电路离散化模型，避免微分方程和复频域转换，离散化的电路可视为不同离散时刻电阻电路的稳态分析，方便电路模型的求解计算。

为了建立柔性直流电网离散模型，首先需要分析电感和电容的离散模型。离散模型需要选取合适的数值积分方法，需要考虑如下3个问题[17]：①数值稳定性问题；②局部截断误差问题；③计算效率问题。在数值稳定性方面，显式积分方法在电路方程为病态微分方程时容易不稳定，隐式积分法具有较好的数值稳定性，后退欧拉法具有A稳定性，梯形积分公式具有对称A稳定性。在局部截断误差方面，若积分步长为h，后退欧拉法的局部截断误差为h2数量级，梯形积分法的局部截断误差为h3数量级，这两种数值积分公式均能满足误差精度要求。在计算效率上，后退欧拉法和梯形积分法计算效率都比较高。因此，离散模型常采用梯形积分法或后退欧拉法进行离散化处理[16]。

采用后退欧拉法构建离散模型，可以得到电容和电感的离散模型，如图4所示，分别表示为

观察式（3）和式（4），可以得到采用后退欧拉法tn+1时刻电容、电感电压与电流的关系。式（3）表明：在tn+1时刻，电容C可等效为一个电导C/h与电流源-CuC,n/h的并联，其离散电路模型如图4（a）所示。式（4）表明：在tn+1时刻，电感L可等效为一个电导h/L与电流源iL,n的并联，其离散电路模型如图4（b）所示。

图4 基于后退欧拉法的离散模型Fig.4 Discrete model based on backward euler method

采用梯形积分法构建离散模型，可以得到电容和电感的离散模型，如图5所示，分别表示为

同理，观察式（5）和式（6），可以得到采用梯形积分法tn+1时刻电容、电感上电压与电流的关系。式（5）表明：在tn+1时刻，电容C可等效为一个电导2C/h与电流源-（2CuC,n/h+iC,n）的并联，其离散电路模型如图5（a）所示。式（6）表明：在 tn+1时刻，电感L可等效为一个电导h/2L与电流源（huL,n/2L+iL,n）的并联，其离散电路模型如图5（b）所示。

图5 基于梯形积分法的离散模型Fig.5 Discrete model based on trapezoidal rule

2.2 MMC离散模型

基于电感、电容离散模型及子模块闭锁前MMC等效电路模型，MMC离散模型可等效成电压源与阻抗串联的戴维南等值电路，如图6所示。

图6 闭锁前MMC离散模型Fig.6 Discrete model of MMC before blocking

采用后退欧拉法构建离散模型，图6中闭锁前MMC离散模型相关参数满足关系

采用梯形积分法构建离散模型，图6中闭锁前MMC离散模型相关参数满足以下关系

2.3 换流站离散模型

基于MMC的柔性直流输电工程均采用单极结构或双极结构，两种结构的柔性直流电网具有不同的故障特性，需要建立不同的等效电路模型[9]。单极直流电网双极短路故障、双极直流电网单极接地和双极短路故障，闭锁前换流站离散模型如图7所示，图中，Zi为第i个换流站的离散阻抗，ui,n为第i个换流站第n次迭代计算时的离散电压，ii,n为第i个换流站第n次迭代计算的离散电流。

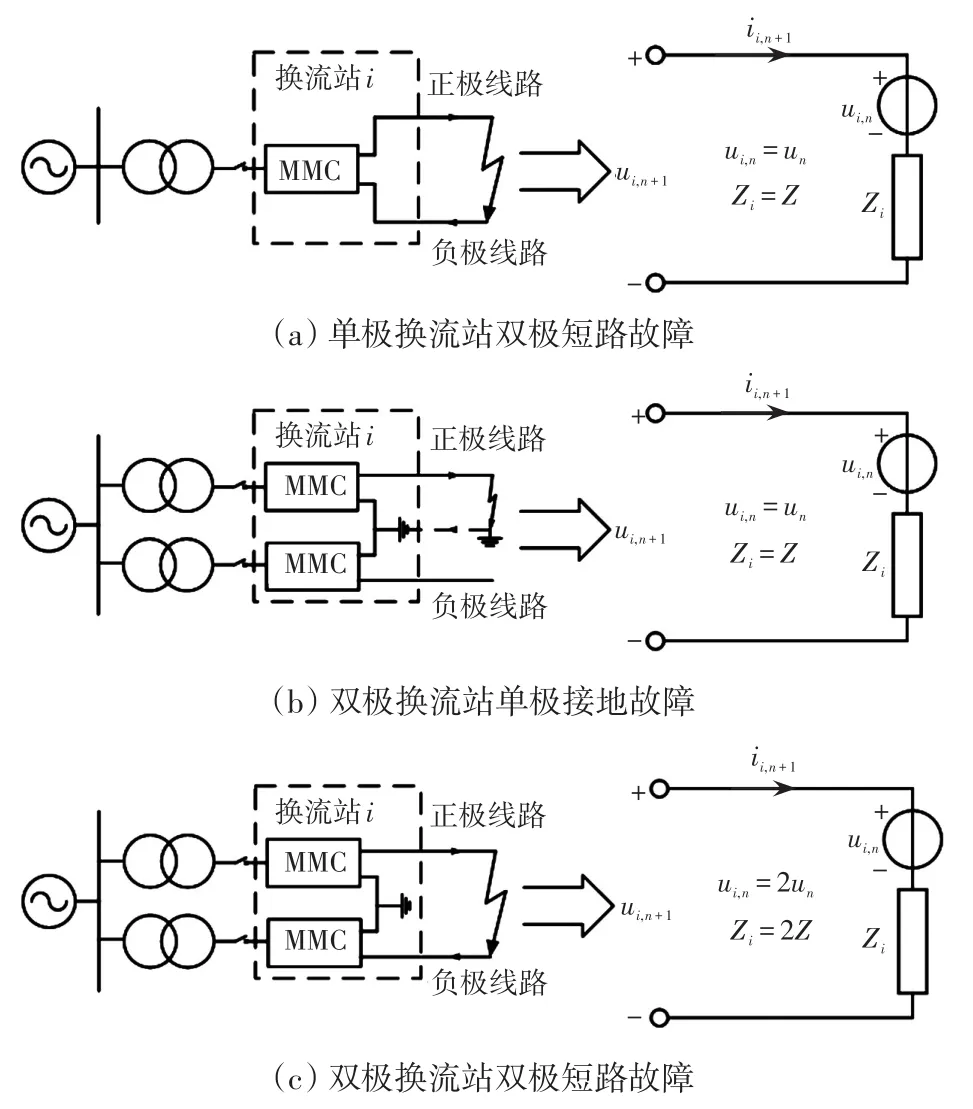
图7 闭锁前换流站离散模型Fig.7 Discrete model of converter station before blocking

单极柔性直流电网发生如图7（a）所示的双极短路故障时，故障电流在换流站中流经整个MMC，此时换流站离散模型相当于闭锁前MMC双极短路故障离散模型。双极柔性直流电网发生如图7（b）所示的单极接地故障时，以正极线路接地为例，故障电流在换流站中流经正极MMC，此时换流站离散模型相当于闭锁前MMC双极短路故障离散模型。双极柔性直流电网发生如图7（c）所示的双极短路故障时，故障电流流经正、负极MMC，此时换流站离散模型相当于闭锁前正、负极MMC双极短路故障离散模型的串联。

2.4 线路离散模型

基于电容和电感离散模型，忽略线路对地电容的作用，可以得到直流输电线路离散模型，如图8所示。图中Zij为第i个换流站和第j个换流站之间线路的离散阻抗，uij,n为第i个换流站和第j个换流站之间线路第n次迭代计算时的离散电压，iij,n为第i个换流站和第j个换流站之间线路第n次迭代计算时的离散电流。另外，Lij和Rij分别为第i个换流站和第j个换流站之间线路的等效电感和电阻。

图8 直流输电线路离散模型Fig.8 Discrete model of DC transmission line

采用后退欧拉法构建离散模型，图8中离散模型相关参数满足关系

采用梯形积分法构建离散模型，图8中离散模型相关参数满足关系

2.5 柔性直流电网离散模型

四端环形双极柔性直流电网示意如图9所示，直流线路上加装了线路电抗器和直流断路器，交流侧配备了交流断路器。假设在换流站2和换流站3之间的正极输电线路上发生单极接地故障，基于换流站和线路的离散模型，可以得到柔性直流电网离散模型，如图10所示。

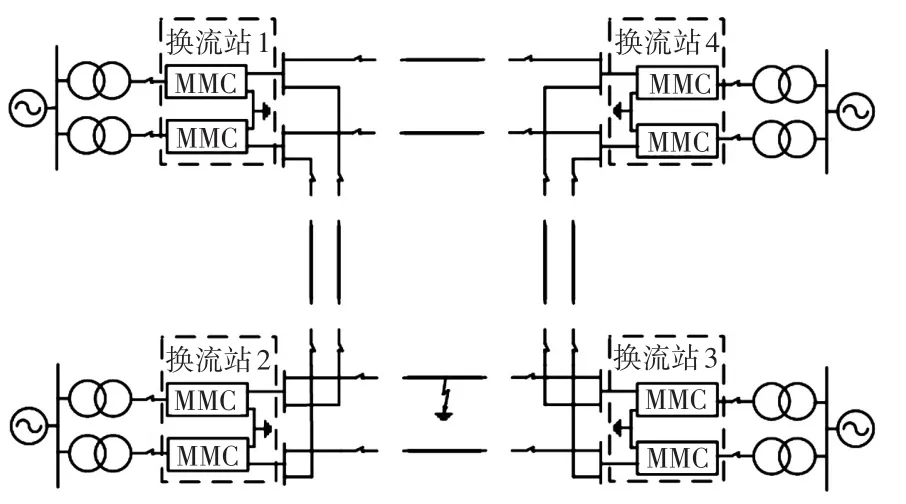
图9 柔性直流电网示意Fig.9 Schematic of VSC-HVDC grid

图10 换流器闭锁前柔性直流电网离散模型Fig.10 Discrete model of VSC-HVDC grid before converter blocking

3 柔性直流电网离散模型的求解与计算

基于图10所示的柔性直流电网离散模型，可以列出直流电网支路电流方程为

植物与水体搭配造景时，植物将水体衬映的尤为美丽。从目前来看，岸边种植柳树与水中铺荷是较为常见的水体植物配置形式。清风拂过柳树，把柳树的枝条吹得摇摇曳曳，清风拂过水面，把水中的波浪吹得波光粼粼，柳树映在水中的倒影与实际景象相互遮掩又映照衬托，丰富了滨水景观，从而给人们带来一种舒适的感觉；池塘中布满粉色的荷花以及碧绿的荷叶，别有一番趣味。在闷热的夏天，若在此驻足观赏，会给人们带来一种清新爽朗的感觉。园林水景和园林小品中经常出现盆栽与池栽相结合的布置手法，满足了人们的观赏需求。

式中：In+1和Il,n+1分别为第n+1次迭代计算时换流站和线路离散电流向量，分别由各换流站和线路的离散电流组成；Un和Ul,n分别为第n次迭代计算时换流站和线路离散模型等效电源向量，分别由各换流站和线路的离散电压组成；Z和Zl分别为换流站和线路离散模型等效阻抗矩阵；A和Al分别为换流站和线路的节点-支路关联矩阵；B和Bl分别为换流站和线路的回路-支路关联矩阵。

In+1和 Il,n+1为待求向量，Un和Ul,n为已知向量，分别定义为

Z和Zl均为以支路阻抗为对角元素的对角阵，分别定义为

A、Al、B和Bl均为依据柔性直流电网离散模型列写的关联矩阵，列写方法不唯一，可以具体表示为

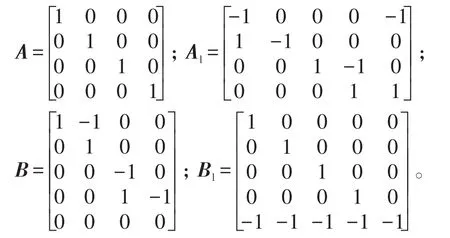
基于柔性直流电网离散等效模型，设计了故障电流数值求解算法，算法流程如图11所示。首先，基于直流电网离散模型，确定系数矩阵A、Al、B、Bl、Z和Zl；基于电路的初始值状态确定出换流站等效电源向量U0和线路等效电源向量Ul,0；基于离散步长h及计算时间设置迭代次数K；然后，通过对式（15）的求解，获得换流站电流向量In+1和线路电流向量Il,n+1，即流经换流站等效电容和电感的电流及线路电感的电流；最后，将电流向量回代入离散公式，更新等效电源向量Un+1和线路等效电源向量Ul,n+1，将更新后的等效电源向量作为下一离散时刻的电路的初始状态，形成迭代过程，直到达到要求的迭代计算次数，即达到要求的计算时间，完成求解计算。

图11 故障电流迭代数值求解算法流程Fig.11 Flow chart of iterative numerical solution algorithm for fault current

4 仿真验证

基于RT-lab仿真平台搭建了如图9所示的四端双极柔性直流电网仿真模型，仿真系统参数如表1所示，换流站间线路长度如表2所示，系统运行参数如表3所示，其仿真步长为25 μs。

表1 仿真系统参数Tab.1 Parameters of simulation system

表2 换流站间输电线路长度Tab.2 Length of transmission lines between converter stations km

表3 系统控制策略Tab.3 System control strategy

采用Matlab软件实现基于离散模型的柔性直流电网短路电流数值计算方法，离散计算步长h设置为25 μs。基于四端柔性直流电网仿真模型，对柔性直流电网不同短路故障类型和不同故障位置的短路电流进行计算，并与详细电磁暂态模型仿真结果进行对比分析，验证所提出的计算方法的精确性。

4.1 单极接地故障计算结果及精确性对比

图12 单极接地故障时短路电流计算值与仿真值Fig.12 Calculated and simulation values of short-circuit current under pole-to-ground fault

在换流站2和换流站3之间线路的不同位置发生单极接地故障，即距离换流站2的距离为线路长度的0%、30%、60%、100%，对故障点两侧的故障电流进行定量误差分析，以仿真数据为基准，采用基于离散模型的柔性直流电网短路电流计算方法故障后10 ms的误差如表4所示。

表4 不同故障位置的单极接地短路故障电流计算误差Tab.4 Pole-to-ground short-circuit fault current calculation errors at different fault positions

通过单极接地短路故障计算值和仿真值的对比，无论采用梯形积分法还是后退欧拉法，计算值与仿真值的最大误差不超过5%，所提方法能够准确获得柔性直流电网单极接地故障的短路电流值。

4.2 双极短路故障计算结果及精确性对比

2 s时，换流站3和换流站4之间线路首端发生双极短路故障，故障发生后10 ms内各条直流线路的故障电流仿真瞬时值和所提方法的计算结果如图13所示。

图13 双极短路故障时短路电流计算值与仿真值Fig.13 Calculated and simulation values of short-circuit current under pole-to-pole fault

在换流站3和换流站4之间线路的不同位置发生双极短路故障，对故障点两侧的故障电流进行定量误差分析，采用基于离散模型的柔性直流电网短路电流计算方法故障后10 ms误差如表5所示。

表5 不同故障位置的双极短路故障电流计算误差Tab.5 Pole-to-pole short-circuit fault current calculation errors at different fault positions

通过双极短路故障计算值和仿真值的对比，无论采用梯形积分法还是后退欧拉法，计算值与仿真值的最大误差不超过5.5%，所提出的方法能够准确获得柔性直流电网极间短路故障的短路电流值。

4.3 单极直流电网双极短路计算结果及精确性对比

为验证此方法对单极直流电网双极短路故障的有效性，将图9所示的双极柔性直流电网改成单极直流电网，其中，MMC、交流系统、直流线路参数保持不变，MCC个数、直流电压等级和换流站传输功率均各减少一半。

2 s时，换流站1和换流站4之间线路首端发生双极短路故障，故障发生后10 ms内各条直流线路的故障电流仿真瞬时值和所提方法的计算结果如图14所示。

图14 单极直流电网双极短路故障电流计算值与仿真值Fig.14 Calculated and simulation values of short-circuit current under pole-to-pole fault in unipolar DC grid

在换流站1和换流站4之间线路的不同位置发生双极故障，对故障点两侧的故障电流进行定量误差分析，采用基于离散模型的柔性直流电网短路电流计算方法故障后10 ms误差如表6所示。

表6 单极直流电网不同故障位置的短路故障电流计算误差Tab.6 Calculation errors of short-circuit fault current at different fault positions in unipolar DC grid

通过双极短路故障计算值和仿真值的对比，无论采用梯形积分法还是后退欧拉法，计算值与仿真值的最大误差不超过4.5%，所提出的方法能够准确获得柔性直流电网极间短路故障的短路电流。

5 结论

本文提出了基于离散模型的柔性直流电网短路电流数值计算方法，通过仿真验证了此方法的准确性，得到如下的结论。

（1）基于后退欧拉法和梯形积分法的换流器电感、电容和线路的离散化模型具有较好的数值稳定性、较小的误差、较高的计算效率。

（2）提出的离散模型和故障电流数值求解算法适用于不同故障类型，具有较好的通用性。

（3）提出的模型和故障电流数值求解算法能够准确获得故障电流，与详细模型仿真结果相比，误差小于5.5%。