双极直觉模糊超图*
龚澍, 高炜
(1.广东科技学院 计算机科学学院,广东 东莞 523083;2.云南师范大学 信息学院,云南 昆明 650500)
图是结构化数据表示的有效模型,用顶点之间的边来刻画数据之间的相互关联;而超图作为图的扩展,在数据表示中起着更重要的作用,应用范围也更加广泛.对于不确定结构化数据,模糊图和模糊超图是广泛而有效的建模手段.模糊图近年来已成为数学和计算机领域的热门研究课题[1-6],尤其是在双极框架[7]中.然而到目前为止,只有少数文献考虑了超图结构中的模糊数据结构.本文将有关直觉模糊超图[8]的概念进行扩展,将其推广到双极直觉模糊超图和双极直觉模糊有向超图框架,并确定了此类超图的一些基本特征;且给出的关于双极直觉模糊超图的相关定义和性质可以直接推广到双极毕达哥拉斯模糊超图.
1 双极直觉模糊超图
在超图框架下,H=(V,E)(或者记为H=(V,A,B))是双极直觉模糊超图,如果下列条件成立:
(1)V={v1,v2,…,vn}是非空有限顶点集合;


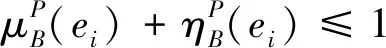
双极直觉模糊集A是初级的,如果它的每个隶属度函数在支集上都是单值的;双极直觉模糊超图是初级的,如果对于每条超边它的正负极直觉模糊关系都是初级的.双极直觉模糊超图称为简单超图,若任何两条超边对应的顶点集合相互不包含,即ei⊆ej⟹ei=ej;称为支集简单超图,若ei⊆ej,supp(ei)=supp(ej)⟹ei=ej;称为强支集简单,若supp(ei)=supp(ej)⟹ei=ej.
对于满足αP+βP≤1和αN+βN≥-1的αP、βP∈[0,1]和αN、βN∈[-1,0],超边e∈E的(αP,αN,βP,βN)-层次超边定义为
H(αP,αN,βP,βN)=(V,E(αP,αN,βP,βN))称为双极直觉模糊超图H的(αP,αN,βP,βN)-层次超图,其中E(αP,αN,βP,βN)={(e1)(αP,αN,βP,βN),(e2)(αP,αN,βP,βN),…,(em)(αP,αN,βP,βN)}.
满足下列条件

(2)若


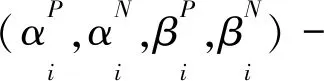
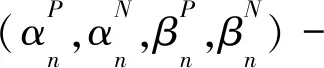
双极直觉模糊超图H′=(V′,E′)=(V′,A′,B′)称为双极直觉模糊超图H=(V,E)=(V,A,B)的部分子图(记为H′⊆H),若下列条件成立:
(1)supp(A′)⊆supp(A)且supp(B′)⊆supp(B);


设H1=(V1,A1,B1)和H2=(V2,A2,B2)是两个双极直觉模糊超图,其中
称H1和H2它们是同态的,若存在同态映射Ψ:V1→V2满足如下两个条件:
(1)对任意v∈V1满足
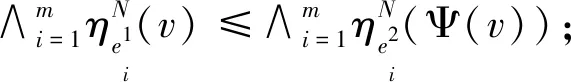



称H1和H2是弱同构的,若存在双射同态满足Ψ:V1→V2,对任意v∈V1满足

(1)对任意v∈V1有


双极直觉模糊超图H的阶(Order)和尺寸(Size)分别定义为
显然,两个同构的双极直觉模糊超图有相同的阶和尺寸,但反过来不成立.此外,根据定义可知,任意两个弱同构的双极直觉模糊超图有相同的阶,而任意两个一致弱同构的双极直觉模糊超图有相同的尺寸,但反过来都不成立.
双极直觉模糊超图H中,顶点v的度表示为
若H1和H2是同构的,Ψ是它们的同构映射,如果v1∈V(H1),v2∈V(H2)满足Ψ(v1)=v2,则有d(Ψ(v1))=d(v2).
由于双极直觉模糊超图之间的同构关系是一种等价关系,满足自反、对称和传递性,因此可以根据同构关系对双极直觉模糊超图进行分类.此外,双极直觉模糊超图之间的弱同构关系是一种偏序关系.
双极直觉模糊超图中长度为t的双极直觉模糊超路P定义为由不同顶点vi和不同超边ei构成的交错序列v1,e1,v2,e2,…,vt,et,vt+1,满足下列条件:

(2)对任意i∈{1,…,t},有vi,vi+1∈ei.
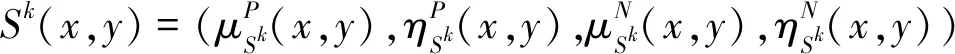

由此,双极直觉模糊超图是连通的当且仅当对任意

强双极直觉模糊超图是指对所有超边ei都满足
的超图.而完全双极直觉模糊超图是指对所有V的子集ei={vi1,vi2,…,vi|ei|},上述四个式子都成立的超图.对于两个同构的双极直觉模糊超图H1和H2:
•H1是连通的当且仅当H2是连通的;
•H1是强的当且仅当H2是强的;
•H1是完全的当且仅当H2是完全的.
如果对任意两条超边ei和ej有下面两个条件成立, 则双极直觉模糊超图称为线性双极直觉模糊超图:
(1)supp(ei)⊆supp(ej)⟹i=j;
(2)|supp(ei)∩supp(ej)|≤1.
双极直觉模糊超图的2-section记为[H]2=(V,A,[B]2),它也是一个双极直觉模糊超图,其顶点集与H一致,超边集定义为{vivj|vi,vj∈ek∈E(H)},即超边是二元顶点集合,两个顶点一同存在于H的某一条超边中.[H]2的边隶属度函数定义为
双极直觉模糊超图H=(V,A,B)的对偶图HD=(VD,AD,BD)定义如下:
•HD的顶点集即为H的超边集,即把H的每一条超边看成一个顶点,H中超边的隶属度函数值即为HD中顶点的隶属度函数值.
•对于H中的每个顶点v,记Ev⊆E是H中包含顶点v的超边集合,它对应HD中的一条超边,且该超边在HD中的隶属度函数表示为
显然,两个同构的超图,它们的对偶也同构.易知,[HD]2=L(H),其中L(H)表示超图H的线图,即H中每条超边看成一个顶点,两个顶点相邻当且仅当在H中对应的两条超边有共同顶点.此外,线性双极直觉模糊超图的对偶也是线性的.
2 双极直觉模糊有向超图
将双极直觉模糊超图的概念扩展到双极直觉模糊有向超图,其本质是将每条超边的顶点集分成两个子集:起点集和终点集.
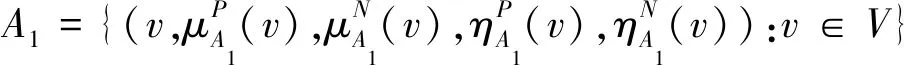
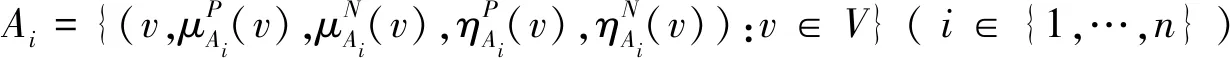
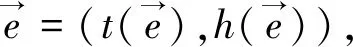


(1)V={v1,v2,…,vn}是非空有限顶点集合;
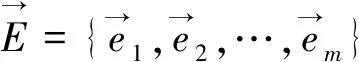
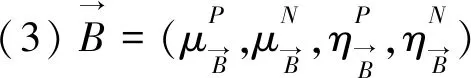
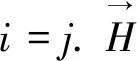
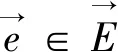

设有序对序列
满足下列条件

(2)若

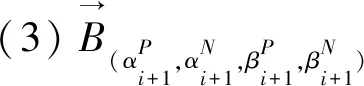

(1)supp(A′)⊆supp(A)且supp(B′)⊆supp(B);
(2)若

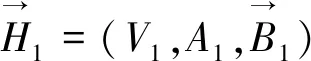
称它们是同态的,若存在同态映射Ψ:V1→V2满足如下两个条件:
(1)对任意v∈V1满足

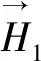
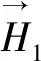
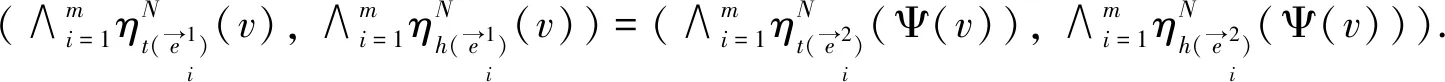
(1)对任意v∈V1有

两个同构的双极直觉模糊有向超图有相同的阶和尺寸;两个弱同构的双极直觉模糊有向超图有相同的阶;两个一致弱同构的双极直觉模糊有向超图有相同的尺寸,但这些结果反过来都不成立.
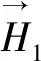
由于双极直觉模糊有向超图之间的同构关系也是一种等价关系,满足自反、对称和传递性,同样可以用于双极直觉模糊有向超图分类.此外,双极直觉模糊有向超图之间的弱同构关系是一种偏序关系.

