解非线性方程组的杂交修正共轭梯度法及其应用*

李丹丹, 王松华

(1.广州华商学院 应用数学系,广东 广州 511300；2.百色学院 数学与统计学院,广西 百色 533000)

非线性单调方程组广泛应用于压缩感知领域中的信号恢复和图像处理等问题[1-2]，是许多工程技术应用的重要工具，其表达式如下：

g(x)=0,x∈Rn，

(1)

-g(xk+αkdk)Tdk≥σαk‖dk‖2，

(2)

其中αk=max{s,ρs,ρ2s,…},σ>0,s>0,ρ∈(0,1);而搜索方向dk的优劣取决于共轭参数的构造形式，在一定程度上决定了算法的收敛速度.

1 算法基础与设计

1.1 投影技术介绍

在共轭梯度投影算法中所使用的投影技术是利用函数g(x)的单调性来构造一个隔离当前迭代点xk与问题(1)的最优解x*的超平面，然后将当前迭代点xk投影到该超平面上，从而产生下一个迭代点xk+1.

对于经典的投影技术[10]，首先寻找一个搜索方向dk，利用线搜索方法产生一个步长αk，使得g(zk)T(xk-zk)>0成立，其中zk=xk+αkdk.由g(x)的单调性，对于问题(1)的任意最优解x*，得g(zk)T(x*-zk)≤0，超平面集合Hk={x∈Rn|g(zk)T(x-zk)=0}，严格分离当前迭代点xk与问题(1)的最优解x*，于是下一个迭代点的更新公式为

(3)

1.2 LCGP算法设计

为了改进HS算法与PRP算法的理论性质，使得所构造的算法同时具备良好的充分下降性与信赖域性质，设计了一个新的杂交搜索方向

(4)

其中共轭参数

(5)

式中,μ>1，yk-1=gk-gk-1.

基于以上论述，给出求解问题(1)的LCGP算法步骤：

步骤1：给定初始点x0∈Rn，正常数s,σ>0,ε,ρ∈(0,1),μ>1.令k∶=0；

步骤2：若‖g(xk)‖≤ε，则算法停止；否则转步骤3；

步骤3：通过式(4)和式(5)计算搜索方向dk；

步骤4：步长αk是由式(2)所决定且令zk=xk+αkdk；

步骤5：若‖g(zk)‖≤ε，则算法停止，并令xk+1=zk；否则，通过式(3)计算新的迭代点xk+1；

步骤6：令k∶=k+1，转步骤2.

2 充分下降性和信赖域特性

引理1由式(4)和式(5)所定义的搜索方向dk，具有充分下降性

(6)

和信赖域特性

(7)

当k≥1时，有

故有

结合式(5),有:

故

(8)

由式(4)和式(8)得

综上所述，式(6)得证.

(ⅱ)当k=0时，式(7)显然成立.

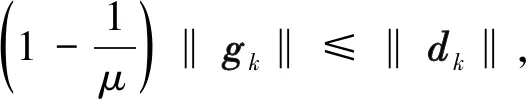
故式(7)成立.

3 全局收敛性分析

作一般性假设A：

(A1)问题(1)的解集非空；

(A2)函数g:Rn→Rn是Lipschitz连续的，即∃M>0，使得

‖g(x)-g(y)‖≤M‖x-y‖，∀x,y∈Rn.

(9)

引理2在假设A条件下，序列{xk}和{zk}是由算法LCGP产生的，那么式(2)产生的步长αk存在下界，即

(10)

引理3的证明类似于文献[11]引理4的证明，故省略.

定理1在假设A条件下，算法LCGP产生的序列{xk}满足以下等式

4 数值试验

使用MATLAB(2014a)编写程序，运行环境为:Windows 10(64bite)，RAM:8 G，CPU3.60 GHz.

4.1 求解非线性单调方程组

在算法LCGP的步骤 2 中，分别采用DFPB1[12]和M3TFR1[13]产生搜索方向，其余步骤与算法LCGP一致，得到算法DFPB1和算法M3TFR1.采用这三种算法求解非线性单调方程组问题.参数设置：s=1,ρ=0.43,σ=0.092,μ=1.96.终止准则为‖gk‖≤10-5，设置算法的迭代次数上限为1 000，维数为3 000，6 000，30 000，60 000，90 000.测试问题来自文献[14]，具体问题和初始点见表1.

表1 测试函数

选用曲线比较法[15]，对三种算法在求解过程中产生的迭代次数、目标函数计算次数和运行时间的数据绘制性能图(如图1).

图1 迭代次数、目标函数计算次数和运行时间性能图

在图1中算法LCGP所对应的曲线均位于算法DFPB1和算法M3TFR1对应的曲线之上，表明LCGP算法在求解大规模非线性单调方程组问题上更加高效与稳定，具有较强的鲁棒性.

4.2 图像恢复问题

表2 算法LCGP和算法DFPB1的恢复图像时间(s)

从左到右分别为20%椒盐噪声图像、算法LCCP恢复的图像和算法DFPB1恢复的图像.

从左到右分别为50%椒盐噪声图像、算法LCCP恢复的图像和算法DFPB1恢复的图像

由表2可知，算法LCGP在CPU时间方面比算法DFPB1有竞争力.此外，由图2和图3可知，算法LCGP和算法DFPB1能够在合理的时间内恢复不同程度受椒盐噪声污染的图像.从而验证了新算法的可行性与实用性.

5 结语

在修正HS算法和修正PRP算法的基础上，设计一个新的杂交搜索方向，结合超平面投影技术和高效的线搜索方法，提出了一个杂交修正共轭梯度算法.该算法具有以下优良的性质：信赖域特性、充分下降性和全局收敛性.采用大规模(维数3 000-90 000)问题进行数值检验，结果表明算法LCGP比算法M3TFR1和算法DFPB1效果更好，具有较强的鲁棒性.此外，将新算法LCGP应用于图像恢复问题，能成功恢复图像，证明新算法具有实际应用价值.