涉及周期移动超平面的全纯曲线差分形式的第二基本定理
蒋静云, 刘晓俊
(上海理工大学 理学院,上海 200093)
1 问题的提出
Nevanlinna[1]在1925年建立了复平面上关于亚纯函数的第二基本定理。文献[2]将其推广到了复射影空间中的全纯曲线上,得到了相应的第二基本定理。2006年,Halburd等[3]证明了有穷级全纯映射涉及差分算子的第二基本定理。
2016年,Cao等[4]证明了在中超级的亚纯映射,取逐点处于N-subgeneral位置的超平面
现考虑用周期移动超平面代替超平面,得到定理1。
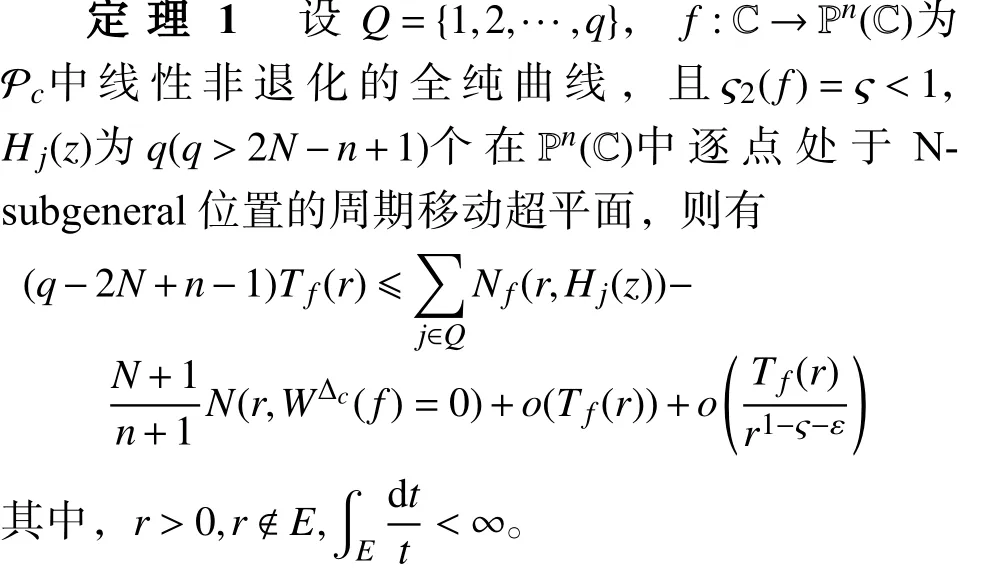
2 符号与定义

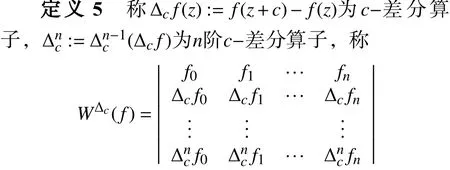
为差分Wronskian行列式。
3 主要引理


这里,证明 因为移动超平面在中逐点处于N-subgeneral位置,所以,对任意






参考文献:
[1]NEVANLINNA R. Zur theorie der meromorphen funktionen[J]. Acta Mathematica, 1925, 46(1/2): 1-99.
[2]RU M. Nevanlinna theory and its relation to Diophantine approximation[M]. Singapore: World Scientific, 2001.
[3]HALBURD R G, KORHONEN R J. Nevanlinna theory for the difference operator[J]. Annales Academiae Scientiarum Fennicae: Mathematica, 2006, 31(2): 463-478.
[4]CAO T B, KORHONEN R. A new version of the second main theorem for meromorphic mappings intersecting hyperplanes in several complex variables[J]. Journal of Mathematical Analysis and Applications, 2016, 444(2):1114-1132.
[5]NOCHKA E I. On the theory of meromorphic curves[J].Doklady Akademii Nauk SSSR, 1983, 269(3): 547-552.
[6]HALBURD R, KORHONEN R, TOHGE K. Holomorphic curves with shift-invariant hyperplane preimages[J].Transactions of the American Mathematical Society, 2014,366(8): 4267-4298.
[7]KORHONEN R. A difference Picard theorem for meromorphic functions of several variables[J].Computational Methods and Function Theory, 2012, 12(1):343-361.
[8]HINKKANEN A. A sharp form of Nevanlinna's second fundamental theorem[J]. Inventiones Mathematicae, 1992,108(1): 549-574.
[9]WONG P, LAW H, WONG P P W. A second main theorem on Pn for difference operator[J]. Science in China Series A: Mathematics, 2009, 52(12): 2751-2758.
[10]杨乐. 值分布论及其新研究[M]. 北京: 科学出版社, 1982.

