产品设计制造环节的结构有序性测度研究
甘 屹, 岳彩晨
(上海理工大学 机械工程学院,上海 200093)
产品的设计制造过程伴随着信息的流动、演化,是信息的采集、传递、加工和利用的演化过程[1]。面对市场无限多样的个性化需求与单个企业有限的资源和能力,企业必须是由合理、有序的信息流、物流、资金流、价值流以及服务流组成跨越时空及思维的有机统一体,能够迅速有效地处理大量复杂信息[2]。关于定量分析产品的设计信息的研究,文献[3-4]提出了一种采用自顶向下设计方法构建的产品TBS(top basic skeleton)模型,并对模型中产品的信息状态进行了分析和测度。文献[5]提出了一种基于本体的多团队协同设计产品的知识建模方法,构建了协同设计知识本体的框架。对于分析产品制造系统内部的信息而言,文献[6]从人因工程的角度分析了制造过程的复杂性。文献[7]在分析动态制造系统排队行为的基础上,提出了两种基于信息熵的制造系统复杂性测度模型。
目前对于开发新产品的研究都是单独以设计或制造环节的信息为研究对象,缺乏对设计制造信息流结构的整体性和连贯性的研究。
本文从制造信息学[1]角度将设计与制造两个环节视作整体进行分析,并充分考虑设计信息与制造信息之间的相互影响,从理论上建立具有一般性的产品信息流结构的有序度和结构熵模型,在实践上定量分析反馈作用对于产品有序度的影响,进一步对产品设计制造信息流进行研究。
1 制造信息学相关理论
1.1 信息熵
在物理学中,熵是表征系统运动复杂程度或系统状态丰富程度的物理量;而在信息论中,熵一般用来描述系统的不确定性和有序程度。按照信息论对熵的定义[8],设离散型随机变量X具有n种可能的取值且各值的概率分别离散型随机变量X的信息熵定义为

其中,信息熵的单位取决于对数底数的选取,通常取2,记作lb,此时单位是bit。信息熵越大,系统的不确定性也越大。
1.2 信息流结构的有序度定义
熵作为一个系统状态的混乱性或无序性的测度,将系统的实时结构熵E与其最大熵Emax之比定义为系统结构的无序度,因此,系统结构的有序度

其中,O越大,表明系统的有序化程度越高。
影响产品设计制造模型的信息流流通的主要指标是流通的时效性和准确性,并且这两者互为消长[9]。用时效度Oe来表示产品设计制造模型的信息流结构在流通时效性方面的有序度,用质量度Oa来表示信息流结构在流通准确性方面的有序度。设这两部分彼此独立,具有可加性,则系统结构的综合有序度

式中:e,a分别为时效和质量关于系统结构的权重系数[10]。
为了计算出Oe和Oa,需要先对产品设计制造模型的信息流的时效性和质量性进行测度,即得到设计制造信息流的时效熵和质量熵,进而计算出系统的有序度。
2 产品设计制造信息流的时效性与质量性测度
为了保证产品设计制造信息的整体质量,必须了解产品设计信息以及制造信息。在云制造环境中,产品的设计制造信息处于分散式的网络环境中。信息的传递包括信息发送与信息反馈。假设信源A发出的信息,其概率空间为
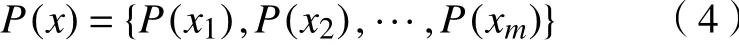
任意1个信息xi的变更将会影响到信源A的整体质量。
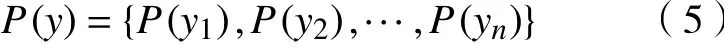
同样地,任意1个信宿yi的变更会影响到信宿B的整体质量。
2.1 产品设计制造信息流及结构熵模型
设产品设计环节的信息流共有n个信息要素。根据信息论原理,以设计环节各个信息要素为信源,其对应的信宿为制造环节的信息要素。设计环节每1个信源在制造环节中都必然有至少1个与之对应的信宿。在某时段内,设计环节向制造环节发出信息,直至制造环节接收到这些信息并对之作出相应处理,此过程中的不确定性称为信息流模型的时效熵,记作Ee。在该时段内,制造环节对信息处理后所发出的反馈信息与原接收信息相一致的不确定性称为设计制造系统信息传递的准确性,该不确定性的测度称为信息流模型的质量熵,记作Ea。
现从产品设计制造过程中信息流演化的时效性和准确性两方面来构建表征设计制造内部信息流结构不确定性的结构熵模型。
在时间段ti内,设计环节提供的信息集合为X(ti, 1),即

设 X(ti, 1, j)表示信源 D1(设计环节)向信宿Mj(制造环节)发出的信息的集合,Q (ti, 1, k)表示设计环节信源D1向制造系统Mk发出的信息的次数。根据古典概率中的古典概型,有
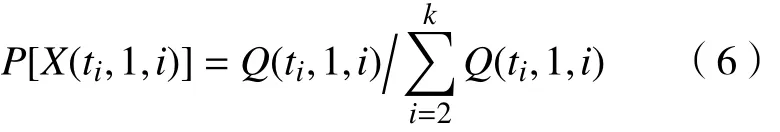
式中:为信源D1向所有信宿发出的信息次数总和;Q(ti, 1, i)为信源D1向信宿Mi发出的信息次数;P[X(ti, 1, i)]表示ti时间段内信源D1向信宿Mi发出信息的概率。
又设同一时间段内,信源D1收到的制造环节各信宿节点反馈的信息集合为Y。
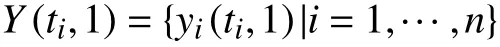
制造环节反馈的信息为F(xi)∈{0, 1}。当取F(xi)=0时,表示信息状态未发生改变,即开环系统;当F(xi)=1时,表示信息状态发生改变,需返回计算上一环节该信息状态下对应的概率,即设计环节接收到制造环节的反馈后,需要及时作出处理。信息流结构熵模型的构建过程中同时考虑了信息传播的时效性与准确性这两个方面,具有动态性。利用结构熵算式可计算出信息传递的时效熵或质量熵。
2.2 信息流结构熵的计算
产品设计制造模型的信息流结构中任意2个信源与信宿的状态实现概率,就是信源到达信宿的流程长度占所有信息流动的流程长度的概率。事实上,产品设计制造环节中的信源与信宿交换信息时是两两交互的。信源与相应的信宿之间的时效熵

式中:Sij为信源xi传递信息至信宿yj所走的路程;Se为信源xi向信宿yj传递信息的总路程;为信源xi传递信息至信宿yj的概率。
在计算Sij时,若信源x1传送信息到y1,则认为信息传送完毕。若信源x2发送信息到信宿y2,则需先发送信息到信宿y1,认为此时Sij=2,该信息发送过程终结。以此类推,Sij=j,当i=j时,发送事件终结。对于时效度而言,信源传递信息至信宿期间走过的路程随信宿数目的增多而增大,反映了信息流通的复杂性。通常情况下,各个信源与信宿之间都会进行信息流动。

只考虑发送事件时,质量熵表示在信息传递中出错机会的不确定性。因此,任意2个信源与信宿之间的信息传递的状态实现概率是产品设计制造中该信息传递的联系跨度占整个信息流结构中总联系跨度的概率。任意信源到信宿y1的跨度均为0,到y2的跨度为1,以此类推。对于质量度而言,信宿与信源之间的跨度反映了信宿对于特定信源的重要程度。跨度越大,表示该信宿对信源的重要程度越小。
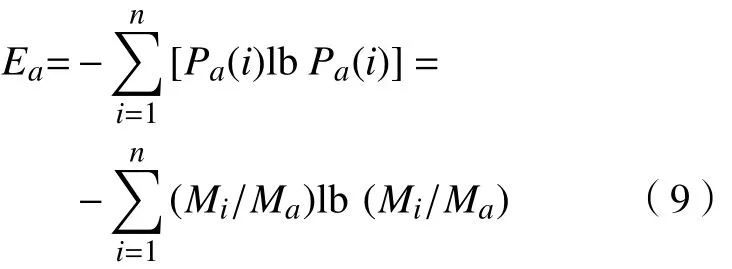
式中:Mi为信源xi发送信息的联系跨度;Ma为信息传递过程中的总联系跨度;Pa(i)为信源xi发送信息成功的概率。

将 Ee,Ea分别代入式(2)和式(3)中,即可得到产品设计制造信息流结构的有序度。
3 应用分析
3.1 结构有序度计算案例
现以典型产品仿人型机器人[11]腿部的设计和制造环节为例,详细分析该产品在整个设计与制造环节中的信息流结构。该机器人腿部能够实现站立、走直线、弯腰及转弯等4个功能。通过构建腿部信息流有序度模型,定量评价设计与制造环节信息流结构的相互关联性。不失一般性,其中左腿部分可以分解为2个功能模块:机械结构和驱动机构。驱动机构的动力靠舵机实现。机械结构如图1所示,舵机安置于各个关节处。根据人体工学数据以及云平台[12]提供的最优资源组合,设计环节信息以及其概率空间如表1所示。设计环节初步的信息状态集DI={形状,高度,位置精度,材料,生产速度}={仿人型,70 mm,1.5 mm,ABS(丙烯腈-丁二烯-苯乙烯),3},即信息X={仿人型,70 mm,1.5 mm,ABS,3}。根据式(4)可得概率空间:P(x)={0.3,0.4,0.3,0.5,1}。
制造环节的操作人员收到产品的设计信息,根据生产条件决定采用某型号3D打印机完成机器人样机的加工。这种3D打印机工作台尺寸固定,为280 mm×180 mm,具有工业打印和生活打印两种用途,并可打印曲面比较复杂的零件。该3D打印机可设置不同的精度数值,包括1.0,1.5,2.0 mm;与该型号打印机配套使用的材料有ABS,PLA(聚乳酸),PVA(聚乙烯醇)。制造环节可以设置的打印速度为40,45,50 mm/s。因此,制造环节信息状态集及其概率空间如表2所示。
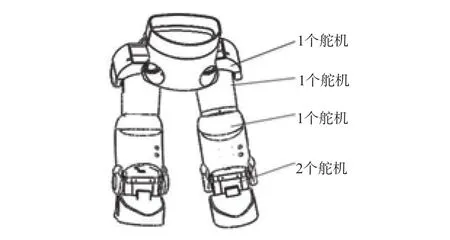
图1 机器人腿部模型Fig.1 Robot leg model

表1 设计环节信息状态及概率空间Tab.1 Design information status and probability space

表2 制造环节信息状态及概率空间Tab.2 Manufacturing information status and probability space
在产品样机的制作过程中,设置生产配置MI={形状,高度,位置精度,材料,生产速度}={仿人型,70 mm,1.5 mm,ABS,40 mm/s},此时3D打印机工作状态良好,但是,所获得的产品易碎。故调整MI={仿人型,70 mm,1.5 mm,PLA,40 mm/s},所获得的产品质量符合要求。将该信息反馈到设计环节,则设计环节的信息状态集更改为DI={仿人型,70 mm,1.5 mm,PLA,40 mm/s}。在这个信息传递过程中,设计环节向制造环节传递信息的开环路程、闭环路程、跨度如表3和表4所示,其中,定义信源x1向信宿y1发送信息时,路程为1,跨度为0,依次类推。
根据式(8)与表3提供的数据计算出Se=15,S11=1,S22=2,S33=3,S44=4,S55=5。
因此,时效熵和最大时效熵分别为
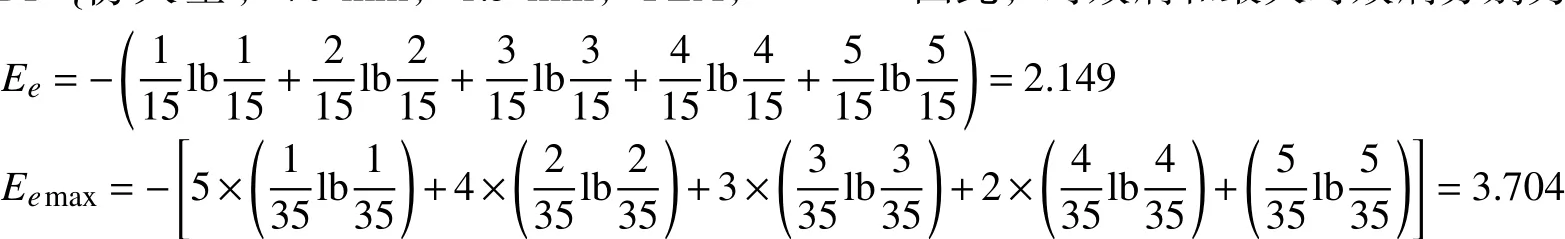
根据式(8)与表3所提供的数据计算出表示加入反馈后信源xi向信宿yj传递信息的总路程。
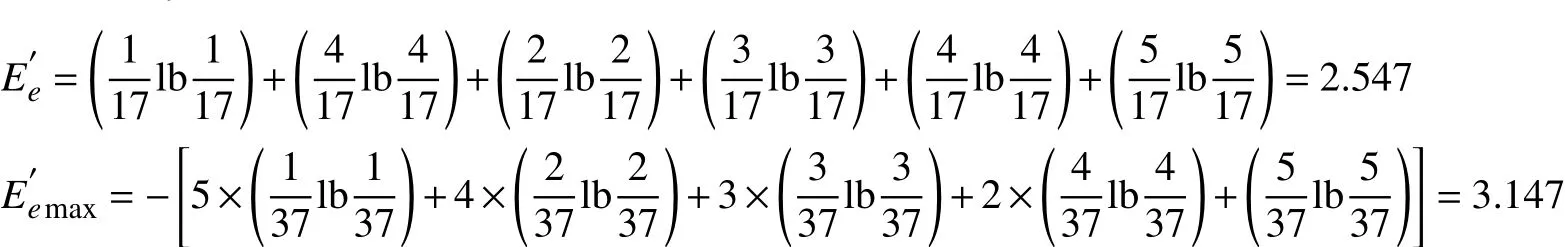

表3 设计制造信息流路程表Tab.3 Schedule of the design and manufacturing information flow

表4 设计制造信息流跨度表Tab.4 Span schedule of the design and manufacturing information flow
根据式(10)与表4所提供的数据,可知Ma=M1+M2+M3+M4+M5=20。My表示信源 xi向信宿yj发送信息的跨度。
由式(9)可计算出设计制造信息流结构的质量熵和最大质量熵
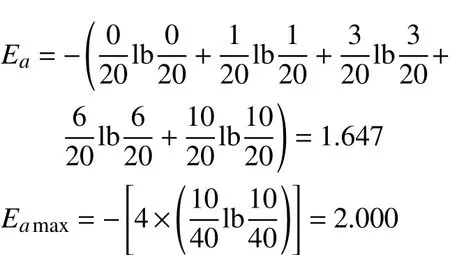
根据式(10)与表4所提供的数据可计算出设计制造信息流结构加入反馈后的质量熵和最大质量熵
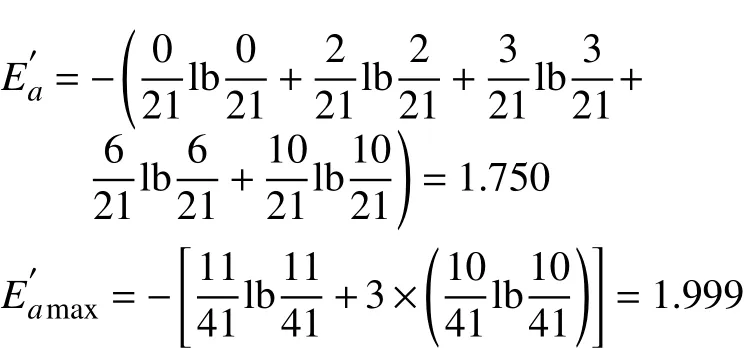
取e=a=0.5,根据式(4)计算信息流有序度,如表5所示。

表5 案例腿部设计制造信息流有序度比较Tab.5 Order degree comparison of the design and manufacturing information flow in the leg case
3.2 分析与讨论
产品设计制造内部信息流结构的复杂度体现了产品结构的复杂性。通过本文的实例可以看出,应用结构有序度和结构熵模型可以定量地描述产品设计制造内部环节之间的信息流。
在上例中,开环与闭环信息流传递的过程基本相似,主要不同的是闭环信息流传递过程中加入了反馈环节,使得结构有序度降低了(0.306~0.151)/0.151×100%≈1.066%。虽然信息流结构有序度与开环时相比降低1%,但是,所获的产品质量更满足要求。闭环传递的产品信息流流经的路程长度是开环传递的117.3%,其时效度比开环传递降 低 了 (0.420~0.177)/0.177×100%≈1.373%, 但是,产品质量得到保证。闭环传递的产品信息流流经的跨度与开环传递的基本相等,但其信息传递的质量度比开环的降低了(1.191~1.125)/1.125×100%≈0.059%。信息闭环传递的质量度基本没变。也就是说,本例中信息的闭环传递在可接受的范围内牺牲了信息流有序度,但能保持信息传递的质量度,更能保证产品质量。
4 结束语
从信息论角度将设计与制造环节的信息状态空间从整体上考虑,提出了一种基于信息熵理论的产品设计制造环节的有序性建模与评价方法,对其复杂性进行测度。通过建立整个环节的信息流结构有序性模型,定量分析了从设计到制造过程中产品信息流的流动状态。通过建立制造环节对设计环节的反馈机制,分别计算了闭环传递和开环传递的信息流有序度,反映了信息反馈对于产品设计制造信息演化的作用。
参考文献:
[1]张伯鹏. 制造信息学[M]. 北京: 清华大学出版社, 2003.
[2]祁国宁, 杨青海. 大批量定制生产模式综述[J]. 中国机械工程, 2004, 15(14): 1240-1245.
[3]甘屹, 陈烁烁, 张雪梅. 基于TBS建模设计中的产品信息状态及其测度分析[J]. 中国机械工程, 2013, 24(16):2131-2135.
[4]GAN Y, HE W M, IHARA T. Analysis for the structure of product manufacturing information flow of cloud manufacturing based on information measurement[J].Journal of Advanced Mechanical Design, Systems, and Manufacturing, 2015, 9(3): JAMDSM0043.
[5]王有远, 王发麟, 乐承毅, 等. 基于本体的多设计团队协同产品设计知识建模[J]. 中国机械工程, 2012, 23(22):2720-2725.
[6]EIMARAGHY W H, URBANIC R J. Assessment of manufacturing operational complexity[J]. CIRP Annals,2004, 53(1): 401-406.
[7]FRIZELLE G, SUHOV Y M. An entropic measurement of queueing behaviour in a class of manufacturing operations[J]. Proceedings of the Royal Society AMathematical, Physical and Engineering Science, 2001,457(2011): 1579-1601.
[8]张志峰, DAVID J. 基于信息熵的单元化制造系统状态度量[J]. 上海交通大学学报, 2015, 49(1): 109-115.
[9]张志峰, 肖人彬. 基于结构熵的生产系统有序性评价的实证研究[J]. 机械工程学报, 2007, 43(6): 62-67.
[10]RONEN B, KARP A. An information entropy approach to the small-lot concept[J]. IEEE Transactions on Engineering Management, 2003, 41(1): 88-92.
[11]张茂川, 蔚伟, 刘丽丽. 仿人机器人理论研究综述[J]. 机械设计与制造, 2010(4): 166-168.
[12]张霖, 罗永亮, 范文慧, 等. 云制造及相关先进制造模式分析[J]. 计算机集成制造系统, 2011, 17(3): 458-468.

