一种用于天线面形恢复测量的无人机导航方案

何凯文， 叶 骞

（上海交通大学 机械与动力工程学院，上海 201100）

新疆奇台将建设110 m口径大型射电望远镜QTT[1]。为保证观测效率，须对其反射面进行实时测量和闭环修正。对于巨型天线，目前多采用远场测量方案[2]。近年来出现了使用无人机进行近场测量的新方法。该方法让无人机携带电磁发射源，在近场平面上飞行并收集位置数据，天线保持静止并收集无人机发出的电磁信号。面形恢复算法利用该信号结合位置数据才可解析出天线的变形，因此，必须获得无人机的位置信息。

针对无人机定位问题，目前部分研究专注于位置传感器的创新，例如使用无线信号的强弱值推算位置[3]。但由于无线信号强度具有有色噪声，导致此法误差较大。更加主流的做法是用视觉里程计辅助传统IMU+GPS导航系统[4]，或者单纯利用SLAM对无人机进行定位和控制[5-8]。此法精度较高，但需要较强的计算能力。此外，更加直接的方法是使用差分GPS （GPS-RTK）测量[9]。这种方法技术成熟，容易实现。

理论上，使用差分GPS直接定位便可获得较高精度的位置数据。但对于天线测量工况，单纯使用差分GPS仍面临很多问题。首先，GPS对卫星信号强度非常敏感。由于天线的遮挡，差分GPS极有可能丢失部分卫星信号，大大影响测量精度。其次，由于机载RTK运算能力的限制，其数据频率普遍较低，不能达到面形恢复的数据密度要求。

为了解决上述问题，需要在飞机上加入另一个绝对位置传感器。双目视觉传感器搭配SLAM算法，由于精度较高，且除光照等条件外对其他因素不敏感，因而非常适合加入此导航系统。为了解决数据频率和GPS受到干扰时的数据可信度急剧下降的问题，必须加入数据融合算法提高数据密度，增加系统可靠性。适用于此应用场合的融合算法有粒子滤波器[10]（PF）、扩展卡尔曼滤波器[11-13]（EKF）和无损卡尔曼滤波器[14]（UKF）等。由于机载计算能力有限，为了保证系统可靠性，本文采用EKF。

差分GPS和视觉传感器相对常规GPS精度更高，常规EKF在此条件下有固有缺陷。一方面，与高精度传感器相对的测量噪声协方差应设置较小值，以使数据权重大，这样容易造成滤波结果趋近直接测量值。另一方面，由于无人机使用环境复杂，系统噪声和测量噪声急剧变动，常规卡尔曼滤波缺乏对噪声的估计[15-17]，可能在后期造成滤波器发散。

相关研究表明，在卡尔曼滤波器中加入自适应模块能够缓解上述问题。目前普遍采用的自适应EKF算法有强跟踪自适应滤波器[18]、Sage-Husa自适应滤波算法[19]、模糊自适应卡尔曼滤波器[20]等。强跟踪自适应滤波器通过在协方差阵中加入衰减因子，使信息序列趋向相互垂直，并且在线调节滤波增益阵。此法对模型不确定系统以及参数时变系统表现出更好的鲁棒性。Sage-Husa自适应滤波算法设计噪声统计估计器估计噪声特性，并将统计信息用于最优预测，改善EKF对变噪声系统的估计性能。其基本使用方法有两种：一种是设置遗忘因子，对计算出的噪声统计信息进行加权处理；另一种是设置比例因子，将方差初值和估计值进行加权。后者在结果的震荡幅值上优于前者，并且可以利用比例因子对其性能进行灵活调整，整体性能更好[21]。

本文基于Sage-Husa算法进行改进，提出一种适用于含有差分GPS和视觉传感器，具有较高可靠性的自适应扩展卡尔曼滤波器。为验证此方案的可行性，本文以六轴无人机作为实验平台，使用ROS进行统筹计算和控制，并搭配GAZEBO仿真平台对自适应卡尔曼滤波器进行参数整定。自适应EKF算法由机载计算机实时计算，并可实时传输位置数据，有望实现天线主动面实时闭环修正。

1 机载传感器架构及系统模型简介

1.1 系统架构

本文所采用的模型有15个状态变量，如图1所示。滤波器一共有5个输入模块，分别对应惯性测量单元、高度计（气压计）、常规GPS、差分GPS和视觉传感器。飞控的加速度计、陀螺仪和地磁计一同组成IMU，提供对应信息，常规GPS作为辅助传感器，对其位置进行差分后作为速度观测量。差分GPS提供水平方向位置信息，视觉传感器提供水平位置和高度信息。上述传感器得到的数据分别导入常规EKF，单独使用差分GPS作为位置估计的常规EKF和本文提出的自适应EKF进行融合，并将自适应EKF的结果导入位置控制器进行闭环控制。

图1 导航系统架构示意图Fig.1 Navigation system structure diagram

1.2 系统模型

设从机体坐标系b到导航坐标系n的旋转矩阵为

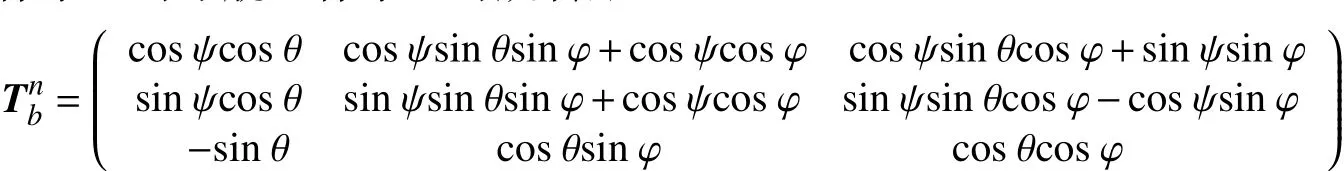
式中，分别表示3个姿态角。本文采用的非线性模型转移公式如下：

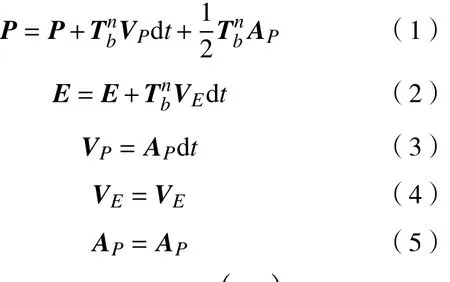
式中：P代表位置向量，即E代表姿态角向量，即和分别为位置速度和加速度向量；为角速度向量；dt表示计算间隔时间。式（1）～（5）由牛顿运动定律配合三维旋转公式变换得到。

2 自适应卡尔曼滤波器

2.1 数据融合的时间策略

此自适应扩展卡尔曼滤波器主要解决两个问题：a. 充分利用差分GPS和视觉传感器，将数据进行有效融合；b. 增加数据密度，提高系统实时性。由表1可知，各传感器的数据频率和精度各不相同。精度较高的双目视觉里程计和差分GPS，其频率只有5 Hz，而气压计和IMU为30 Hz。如果让EKF等待所有数据到达才计算，将不能满足系统实时性以及数据密度的要求。考虑到机载计算机的计算能力，通过实验发现，卡尔曼滤波器工作频率为20 Hz时最高效。

本文对如下两种时间策略进行了对比：

a. 仅使用差分GPS数据作为绝对位置数据，在中途的运算过程中，RTK没有更新数据，则认为观测数据不变；

b. 间隔采用差分GPS和视觉里程计的加权平均数据（当前时刻数据权重0.9，上一时刻数据权重 0.1）。

对于第二种策略，系统每一个完整运行周期为0.2 s，图2为其运行示意图。30.1 s时，差分GPS数据更新，并与上一时刻视觉里程计数据加权平均后作为观测值；30.15 s时，传统GPS数据更新，采用30.1 s的加权平均值作为位置观测数据；30.2 s时，视觉里程计的数据更新，与30.1 s差分GPS数据加权平均，作为位置观测数据；30.25 s时，传统GPS数据更新，采用30.2 s采集的加权平均值作为观测数据，至此完成一个运行周期。此策略相当于用2个5 Hz传感器合成1个10 Hz传感器。

表1 传感器静态测试性能数据Tab.1 Static test performance data of the sensor

图2 时间策略运行示意图Fig.2 Time strategy running diagram

2.2 数据震荡问题

若使用常规EKF，为了让融合结果向正确结果收敛，差分GPS和视觉里程计的过程噪声方差设置值应当远小于传统GPS和气压计。两个高精度传感器的权重相近，但它们的数据并不总是相近。因此滤波器输出值可能会在差分GPS和双目视觉传感器的数据之间震荡，如图3所示。

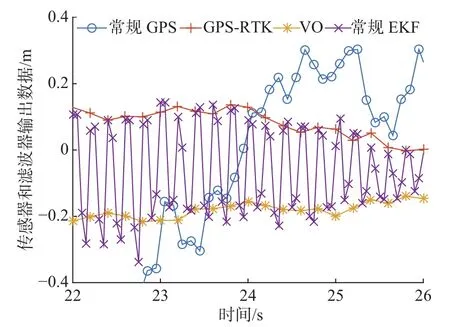
图3 数据震荡示意图Fig.3 Data concussion diagram

此外，GPS信号还非常容易受环境影响。如果测量噪声方差阵为常量，则当差分GPS数据发生较大变动时，系统输出值将随之偏离正确值，无法收敛。

在测量过程中，差分GPS和视觉里程计的数据会随机地相互靠近或远离。间隔采用差分GPS和视觉里程计本质上是给观测值加入时变噪声，使之成为变噪声序列。

2.3 自适应扩展卡尔曼滤波器

为了解决上述问题，充分利用差分GPS和视觉里程计的数据，必须在常规EKF中加入改进的带噪声统计估计器的Sage-Husa自适应滤波器。

文献[17]给出了Sage-Husa提出的无偏递推噪声统计估计器公式，系统噪声方差估计公式为

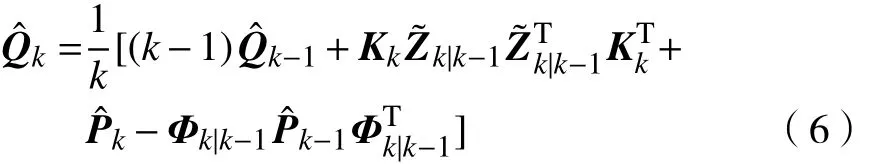
式中：k表示时刻；为k时刻系统噪声协方差矩阵最优预测值；为k时刻卡尔曼增益矩阵；为测量残差一步预测值；为k时刻协方差矩阵最优预测值；为非线性系统方程的泰勒展开一阶项对应的转移矩阵。

测量噪声方差估计为

式中：为k时刻系统测量噪声协方差矩阵最优预测值；为非线性测量方程的雅可比矩阵。

式（6）～（7）的本质是对噪声统计信息进行算术平均。随着k增大，测量噪声和系统噪声都将趋于某固定值。此值包含前k个时刻的噪声统计特性，对噪声的估计表现出较好的性能。由于输入的观测值带有时变噪声，因而当噪声变动时，此估计器不能快速跟踪噪声变化。从优化性能考虑，应当重视新近数据。现将改进的自适应算法详述如下。

设系统方程：

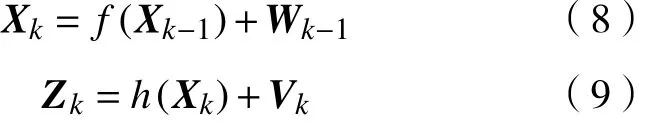
式中：是系统k时刻状态向量；是系统k时刻测量向量；表示系统非线性方程；表示测量方程；为系统噪声序列；为测量噪声。满足的条件为

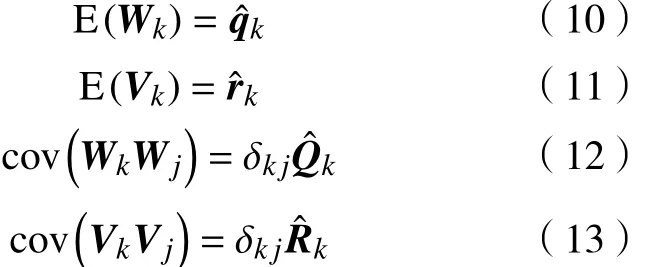
式中：E表示期望；cov表示协方差；为k时刻系统噪声最优预测值；为k时刻测量噪声最优预测值；为

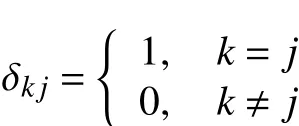
将式（6）～（7）简化后可得

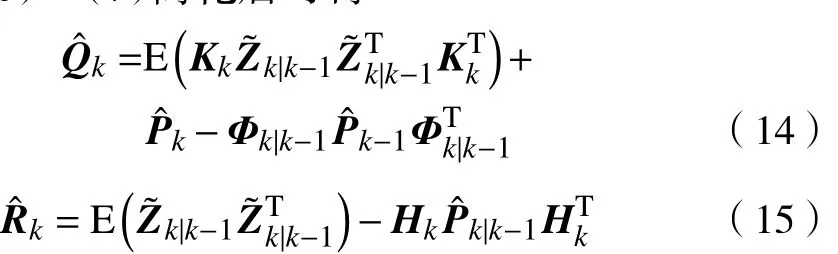
传感器采样全周期（所有传感器都更新一次数据）为0.2 s，而卡尔曼滤波器运行周期为0.05 s。因此希望当前时刻的噪声计算受到前3个时刻的影响。用a1和a2分别表示对测量噪声协方差阵和过程噪声协方差阵添加的比例因子，将Sage-Husa采用的公式改进如下：

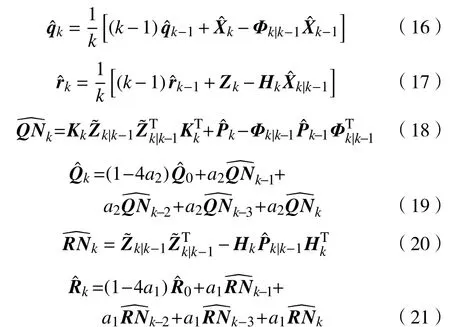
式中，为按照简化后的Sage-Husa噪声统计公式进行计算的最优预测值作为初值，其取值与常规EKF采用的系统和测量协方差阵相同。对于两个矩阵，由于以4次卡尔曼滤波器计算为周期进行，所以在计算这两个矩阵时加入前面3次计算的结果，进行平均。实验发现，此自适应EKF的初值敏感程度低于常规EKF，只要比例因子a1和a2设置恰当，此噪声模型会自动调节。

此卡尔曼滤波器的运行过程与常规扩展卡尔曼滤波器相似，只是在传统方法的基础上增加了噪声统计估计器相关项（考虑到机载运算能力，本文直接采用线性化方程进行计算）。

a. 预测阶段。

在状态一步预测时加入系统噪声预测：

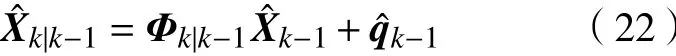
在协方差一步预测时加入系统噪声方差估计：

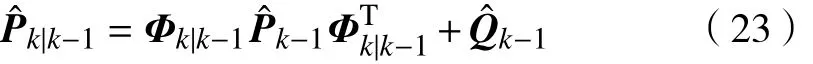
其中，和由上一轮对实变噪声统计计算得到。

b. 更新阶段。

计算最优卡尔曼增益阵时加入测量噪声方差预测：

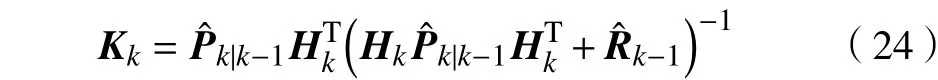
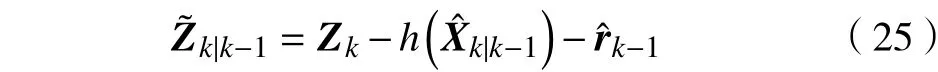
和为上一轮计算得到的测量噪声估计值。

最后进行最优状态估计与协方差更新，与常规卡尔曼滤波相同。

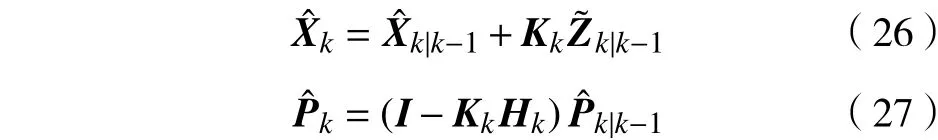
3 多传感器数据融合实验

3.1 仿真实验

仿真时同时运行3种滤波器：采用第二种时间策略的常规EKF；采用第一种时间策略、仅使用差分GPS数据的常规EKF；采用第二种时间策略的自适应EKF。后文将它们分别简称为常规滤波器、差分GPS常规滤波器和自适应滤波器。

仿真过程中，在真值基础上加入与真实传感器特性相同的噪声作为测量值。图4为仿真情况下的设定轨迹、真实轨迹和滤波器输出轨迹的三维对比图。

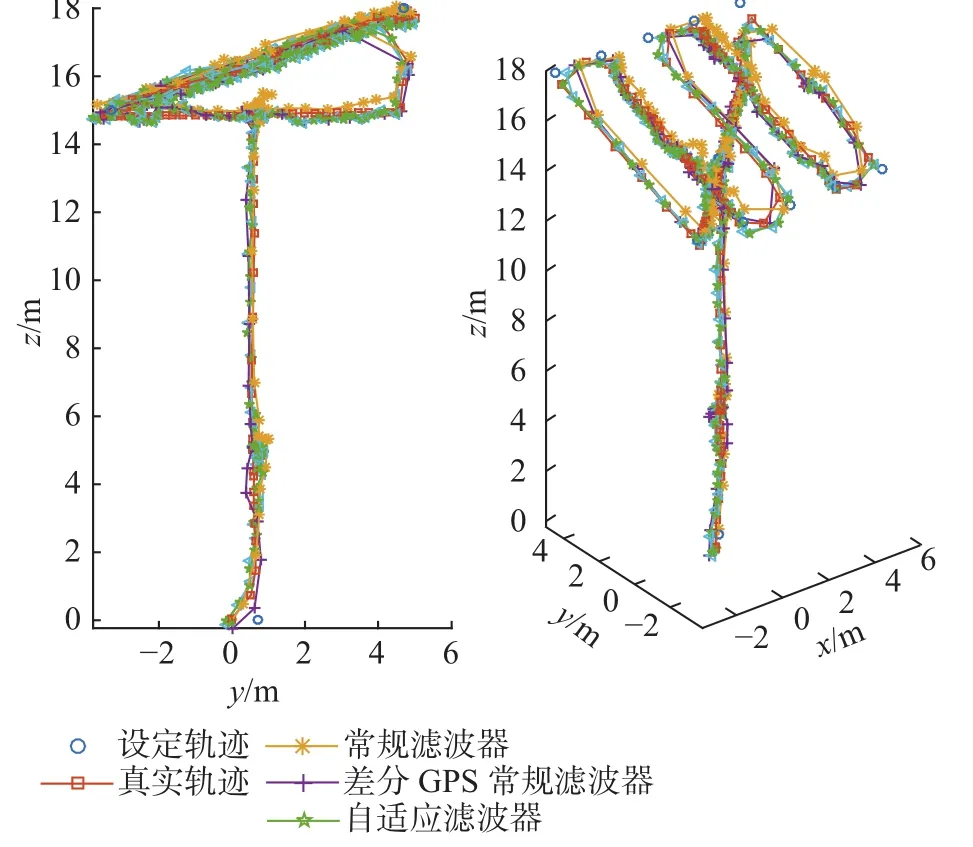
图4 仿真轨迹图Fig.4 Trajectories in the simulation

考虑天线工作时口径面为一斜面，因而将测试轨迹设置在一个与口径面平行的斜面上，如YZ坐标系的图像（图4左图）所示。经过多组仿真实验可知，当a1=0.05～0.07，a2=0.05～0.06时，自适应滤波器效果最好。图5是各传感器和滤波器输出的X轴位置随时间变化的曲线。

图5 仿真实验X轴输出对比图Fig.5 Comparison of the X-axis simulation outputs

将74～79 s的图像放大，如图6所示。虚线表示常规滤波器数据在两个传感器之间震荡。差分GPS常规滤波器输出数据仅在差分GPS数据周围波动，精度反而不如直接测量结果。受益于噪声估计器，图中最贴近真实轨迹的实线便是自适应滤波器数据。表2是仿真阶段各传感器和滤波器输出数据误差的统计信息。

标准差的柱状对比图如图7所示。从误差标准差数据可以看出自适应滤波器在X，Y，Z 这3轴的数据波动最小，最贴近真实值。表2 仿真数据误差统计信息

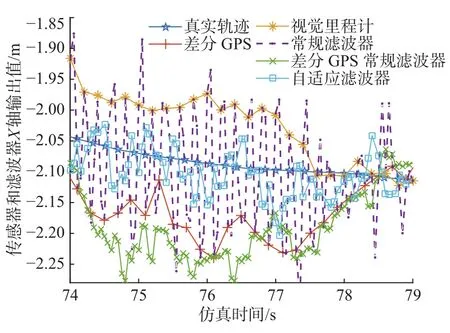
图6 仿真实验X轴输出放大图Fig.6 Enlarged figure of X-axis simulation outputs

Tab.2 Error statistic information in the simulation

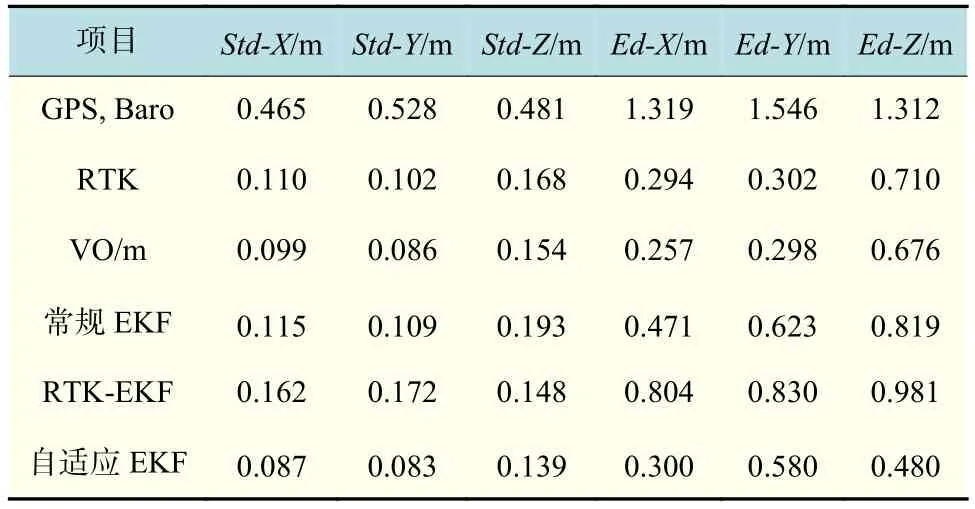
注：表中RTK-EKF即差分GPS常规滤波器。

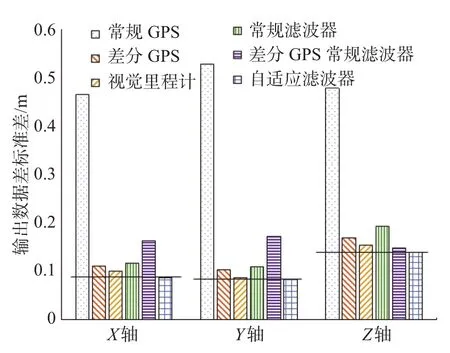
图7 误差标准差对比图Fig.7 Comparison of MSE

3.2 实际飞行测试

本文采用的实验平台如图8所示。由于飞机的计算能力有限，在实际飞行测试时只在飞机上运行自适应滤波器程序。无人机在测量时依照航点飞行，航点间隔0.2 m，在航点之间会以非常缓慢的速度飞行。图9～10便是在此真实测量状态下的轨迹（图9为俯视图，图10为左视图）。由于飞行缓慢，加上风扰，导致真实飞行轨迹与设定航迹之间偏差最大达到1 m左右。

图8 六轴无人机实验平台Fig.8 Six-axis UAV experimental platform

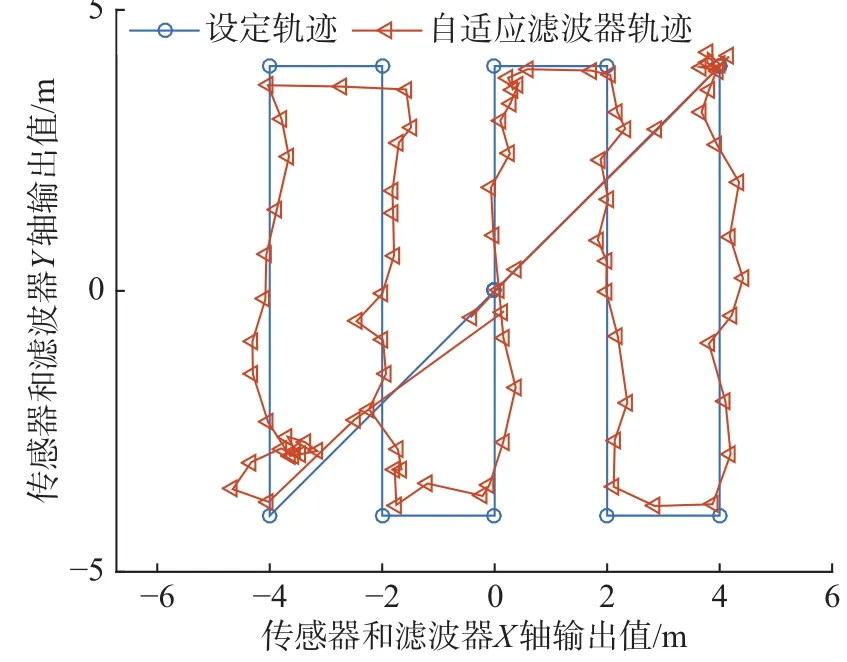
图9 设定轨迹与滤波器输出轨迹对比（X-Y轴）Fig.9 Comparison of the preset trajectory and filter output trajectory (X-Y Axis)

图10 设定轨迹与滤波器输出轨迹对比（Y-Z轴）Fig.10 Comparison of the preset trajectory and filter output trajectory (Y-Z Axis)

图11 则是飞机在不设置航点，连续飞行时测得的X轴各传感器和滤波器输出值对比图和轨迹俯视图（右上角小图）。其中，差分GPS常规滤波器和自适应滤波器数据使用采集数据离线运行得到。由图11可知常规滤波器效果与仿真相似，即在差分GPS和视觉里程计间震荡。差分GPS常规滤波器的数据仅受差分GPS的影响，而自适应滤波器的数值在差分GPS和视觉里程计之间，曲线较平滑。

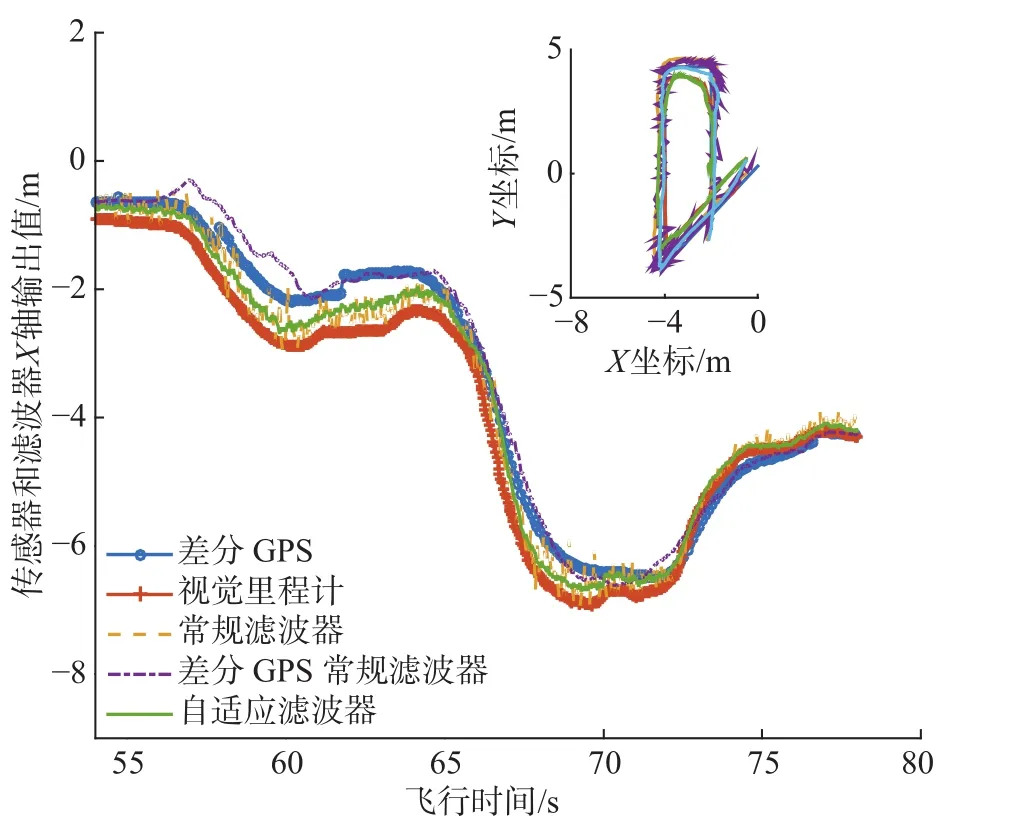
图11 连续飞行实验X轴输出对比Fig.11 Comparison of X-axis outputs in the continuous flight test

3.3 弱GPS信号的实验数据分析

在楼宇间的空旷场地进行弱GPS信号条件下的实验（考虑到实验的危险性，此实验只在地面移动飞机），测得X轴数据随时间变动的图像如图12所示。

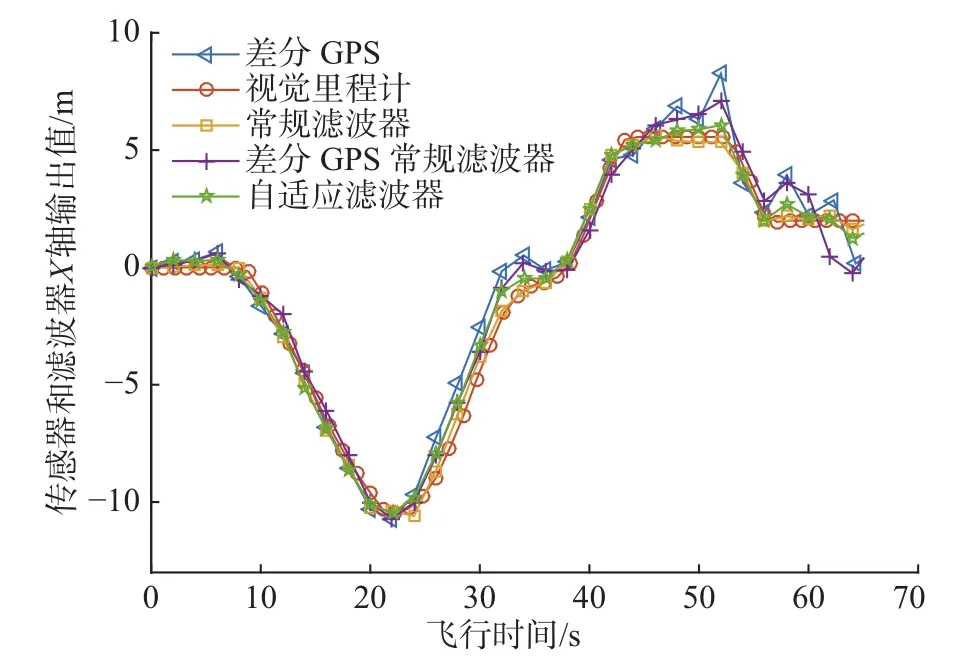
图12 弱GPS信号实验X轴输出对比Fig.12 Comparison of X-axis outputs in the weak GPS signal test

楼宇对GPS信号影响较大，由图12可知差分GPS和常规GPS数据都出现一定波动，甚至丢失信号。此时可信度最高的数据为视觉里程计。由图13可知，当差分GPS数据剧烈波动时，差分GPS常规滤波器依然跟随它，导致较大的数据偏差。而由于加入了自适应噪声调整模块，虽然仍受一定影响，但自适应滤波器的数据更加趋向于稳定的视觉里程计。此情况间接表明，自适应滤波器能够在某传感器数据出现波动时趋向更加可信的数据，从而保证了位置测量精度和系统可靠性。

图13 弱GPS信号实验X轴输出放大图Fig.13 Enlarged figure of comparison of X-axis outputs in the weak GPS signal test

4 结 论

本文从工程应用角度出发，为满足天线主动面实时闭环修正要求，针对差分GPS和视觉里程计两种外部传感器数据频率低，GPS信号容易被天线遮挡而受干扰的问题，提出一种用于无人机的多传感器导航方案。此方案对Sage-Husa自适应扩展卡尔曼滤波器进行改进，内容包括传感器数据输入的时间策略、噪声统计特性算法，并通过仿真和实际飞行测试对系统的实际导航性能进行了对比验证，结论如下：

a. 自适应扩展卡尔曼滤波器通过融合各种传感器信息，将数据频率提高到20 Hz，并结合自动控制系统实现沿设定轨迹自动飞行，基本能够满足天线测量需要。

b. 弱GPS信号情况下的测试结果表明，自适应滤波器和视觉传感器的组合能够在一定程度上缓解差分GPS数据波动对系统造成的影响，其可靠性明显优于常规卡尔曼滤波器。

c. 本文对比了常规卡尔曼滤波器和改进的自适应滤波器。由于自适应模块加入，自适应滤波器在充分利用了高精度传感器的基础上，数据精度、稳定性和可靠性方面都优于常规滤波器。

参考文献：

[1]王娜. 新疆奇台110米射电望远镜[J]. 中国科学： 物理学力学 天文学, 2014, 44(8)： 783-794.

[2]BAARS J W M, LUCAS R, MANGUM J G, et al. Nearfield radio holography of large reflector antennas[J]. IEEE Antennas and Propagation Magazine, 2007, 49(5)： 24-41.

[3]LUO C B, MCCLEAN S I, PARR G, et al. UAV position estimation and collision avoidance using the extended Kalman filter[J]. IEEE Transactions on Vehicular Technology, 2013, 62(6)： 2749-2762.

[4]ANGELINO C V, BARANIELLO V R, CICALA L. UAV position and attitude estimation using IMU, GNSS and camera[C]//Proceedings of the 2012 15th International Conference on Information Fusion. Singapore： IEEE,2012： 735-742.

[5]KIM J, SUKKARIEH S. Real-time implementation of airborne inertial-SLAM[J]. Robotics and Autonomous Systems, 2007, 55(1)： 62-71.

[6]周璠, 郑伟, 汪增福. 基于多异类传感器信息融合的微型多旋翼无人机实时运动估计[J]. 机器人, 2015, 37(1)：94-101.

[7]夏凌楠, 张波, 王营冠, 等. 基于惯性传感器和视觉里程计的机器人定位[J]. 仪器仪表学报, 2013, 34(1)：166-172.

[8]曹美会, 鲜斌, 张旭, 等. 基于视觉的四旋翼无人机自主定位与控制系统[J]. 信息与控制, 2015, 44(2)： 190-196.

[9]谢德胜, 徐友春, 万剑, 等. 基于RTK-GPS的轮式移动机器人轨迹跟随控制[J]. 机器人, 2017, 39(2)： 221-229.

[10]RIGATOS G G. Nonlinear Kalman filters and particle filters for integrated navigation of unmanned aerial vehicles[J]. Robotics and Autonomous Systems, 2012,60(7)： 978-995.

[11]HIDE C, MOORE T, SMITH M. Adaptive Kalman filtering for low-cost INS/GPS[J]. Journal of Navigation,2003, 56(1)： 143-152.

[12]刘洪剑, 王耀南, 谭建豪, 等. 一种旋翼无人机组合导航系统设计及应用[J]. 传感技术学报, 2017, 30(2)：331-336.

[13]安雷, 张国良, 张维平, 等. 移动机器人扩展卡尔曼滤波定位与传感器误差建模[J]. 信息与控制, 2012, 41(4)：406-412.

[14]ABD RABBOU M, EL-RABBANY A. Non-linear filtering for precise point positioning GPS/INS integration[J]. IPRS - International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2014, XL-2： 127-132.

[15]王龙, 章政, 王立. 改进扩展卡尔曼滤波的四旋翼姿态估计算法[J]. 计算机应用, 2017, 37(4)： 1122-1128.

[16]田易, 孙金海, 李金海, 等. 航姿参考系统中一种自适应卡尔曼滤波算法[J]. 西安电子科技大学学报, 2011,38(6)： 103-107, 122.

[17]魏伟, 秦永元, 张晓冬, 等. 卡尔曼滤波系统和量测噪声自适应估计的关联性[J]. 测控技术, 2012, 31(12)：98-103.

[18]YIN Z G, LI G Y, DU C, et al. An adaptive speed estimation method based on a strong tracking extended Kalman filter with a least-square algorithm for induction motors[J]. Journal of Power Electronics, 2017, 17(1)：149-160.

[19]SAGE A P, HUSA G W. Algorithms for sequential adaptive estimation of prior statistics[C]//Proceedings of 1969 IEEE Symposium on Adaptive Processes (8th)Decision and Control. University Park, PA, USA： IEEE,1969.

[20]TSENG C H, LIN S F, JWO D J. Fuzzy adaptive cubature Kalman filter for integrated navigation systems[J]. Sensors,2016, 16(8)： 1167.

[21]魏伟, 秦永元, 张晓冬, 等. 对Sage-Husa算法的改进[J].中国惯性技术学报, 2012, 20(6)： 678-686.