基于图像拼接的可信图像修补方法
孙佳忆, 曹 芳, 唐振军, 姚 恒, 秦 川
(1. 上海理工大学 光电信息与计算机工程学院,上海 200093; 2. 广西师范大学 广西多源信息挖掘与安全重点实验室,桂林 541004; 3. 上海海事大学 信息工程学院,上海 201306)
图像修复在许多应用领域中得到越来越多的关注,它被用来删除不想要的物体或区域,填补图像中的缺失部分[1],在计算机视觉研究中也有广泛的应用,包括在图像恢复、压缩、编辑和合并等方面。图像修复也扩展到与图像相关的应用程序中,如它被应用于视频和动画的完成与合并。在过去的几十年中,已经提出了几种图像修复的经典算法。如今的图像修复算法以自修复为主,大概分为两大类。一类是针对小区域破损图像的修复方法[1-4]。例如,Bertalmio等[1]提出的BSCB(Bertalrnio, Sapiro, Caselles, Ballester)算法,该算法基于偏微分方程,利用受损区域周围像素信息来对受损区域进行修复。Chan等[2]提出的基于曲率驱动扩散模型(curvature driven diffusion,CDD)和全变分模型(total variation,TV)[3]是对破损区域进行平滑修复,这类方法对大区域损坏图像的修复会产生模糊等不好效果。另一类是针对大区域破损图像的修复[5-11],这类方法基于图像的纹理和结构进行修复。Drori等[5]突破了上一类模型中只利用破损区域附近像素的弊端,以多个像素组成的小块为单位,修复图像的破损区域。其中,这类算法中较为经典的算法有Criminisi等[6]在2003年提出的一种通过置信度和结构性函数来决定修复优先权并选出最佳匹配块的算法。该算法在纹理复原方面比文献[5]所采用的方法效果更好,但若图像的待修复区域中存在明显的结构特征,仍可能无法得到满意的修复效果。
现有的大多数图像修复方法都是对单幅图像进行的自修复,即通过待修复图像上的未破坏像素对待修复区域进行修复。这类算法有各自的优势,但也面临相同的问题,就是由于缺少可信信息使图像的修复结果非常不稳定,且待修复区域越大越复杂,图像的修复结果就越不能保证。尽管一些现有的修复方法获得了较为理想的视觉修复效果,但也只是在肉眼观察下似乎比较合理,无法保证其真实性,即这种自修复的图像修复算法并不能做到恢复场景的真正面目。
现如今,图像拼接技术以及各种图像处理技术不断发展[12-15],完全可以选择一些合适的相关图像信息作为参考,利用这些参考图像对破损图像进行可信修补,以避免对修复区域做无根据的揣测,可以保证修复的真实性。引入相关图像的过程使恢复图像的真正面目成为可能,直接增加了图像恢复的可信度。但有时并不能通过参考图像获得足够的恢复破损区域的有用信息,这时既无法通过参考图像直接完成破损图像的修复,又不想放弃现有的参考图像而完全靠自修复获得可信度很低的修复结果。所以本文针对大区域破损且存在可供参考的图像的待修复图像,提出了一种自修复和在参考图像协助下的可信修补相结合的图像修复方法。
1 可信修补算法
为了尽可能恢复含有较大破损区域的待修复图像真正面目,并且待修复图像的部分破损区域存在可利用的参考图像作为前提条件,依托图像拼接技术和图像修复算法提出了一种自修复和在参考图像协助下的可信修补相结合的图像修复方法,其框架流程如图1所示。

图1 可信图像修补方法流程图Fig.1 Flowchart of the proposed trustable image inpainting method
本方法是利用参考图像对待修复图像进行可信修补。具体来讲,先提取待修复图像和参考图像中的特征点,再对两幅图像中的特征点进行配对,得到相应的特征点对集,对点对集中的特征点对进行筛选,最终完成待修复图像和参考图像的配准并获得相应的投影矩阵,利用投影矩阵将参考图像中对应的像素信息投影到待修复图像中,完成对破损区域的可信修补。若有多幅参考图像分别是针对多个破损区域,便依次利用这些参考图像分别对相应的破损区域进行修补。若完成以上操作后,发现依然存在未修补的破损区域,而没有对应的参考图像,这时就借助图像修复算法进行图像自修复。
1.1 特征点的提取与匹配
基于参考图像的可信图像修复是待修复图像和移位参考图像拼接的过程。图像拼接的关键为图像配准,而配准的第一步就是提取特征点并完成特征点的粗略匹配。首先,分别提取破损图像和参考图像的特征点,从而抓住两幅图像中主要特征的具体位置,并对特征进行描述、区分和配对。提取特征点的算法有多种,比如SIFT(scale invariant feature transform)特征点提取算法[16]、SUSAN(smallest univalue segment assimilating nucleus)特征点提取算法[17]和Harris特征点提取算法[18]。由于本文研究的问题中待修复图像与参考图像重叠区域大小不定,可能是整个场景的重叠,也可能只是想利用参考图像里的一个事物,所以在选择提取特征点的算法上要关注算法的稳健性和多量性。
Lowe[16]2004年提出了SIFT算法,该算法提取的特征点具有以下特征:提取的是图像的局部特征,具有良好的稳健性;对平移、尺度缩放、旋转、仿射变换、遮挡,甚至亮度变化和噪声都有很好的抵抗能力;提取的特征点数目众多,即使被处理的图像中物体较少,也会产生大量特征点和对应的特征向量。该算法提供了丰富的信息量,非常适用于本文中待修复图像和参考图像的特征提取工作。具体过程如图2所示,该算法在大量的特征信息中,能够快速且准确地完成粗匹配,且运行速度较快,几乎可达到实时的效果。

图2 基于参考图像的修补过程Fig.2 Inpainting process based on a reference image
SIFT算法包含两个阶段:阶段一是特征点的提取和特征向量的生成;阶段二是对特征点进行配对。
其中,特征点的提取步骤如下:
a. 构造高斯金字塔,再做出DOG(difference of Gaussian)金字塔,检测尺度空间极值点。
DOG的表达式为

式中:σ是尺度坐标;(x, y)是空间坐标;L(x, y, σ)是二维图像的尺度空间。图3是由高斯金字塔算出的DOG金字塔的过程。
b. 极值点精确定位。
对三维二次函数进行拟合,从而获得极值点的位置和尺度;然后对得到的极值点进行筛选,先去除对噪声敏感或低对比度的像素点,再去除位于边缘的像素点。方法如下:通过对比度对特征点进行筛选,D ( x, y, σ )的泰勒展开式为

式中:D是某像素点的 DOG结果;x是待选像素。由此便可求得

可通过对设置阈值,便可筛去对比度低的特征点。去除边缘点是通过海森边缘检测,矩阵公
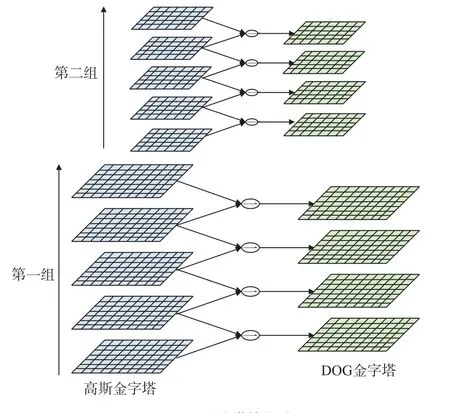
图3 DOG金字塔转化过程Fig. 3 Transformation process of DOG pyramid
式为

筛选公式为

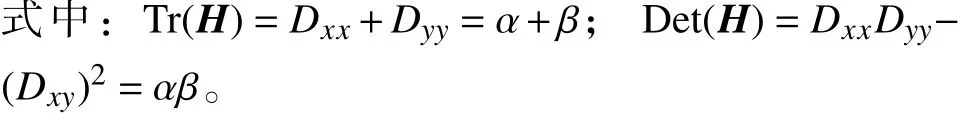
c. 确定特征点方向。
SIFT 算法是通过特征点周围像素的梯度特征为特征点赋予特征向量,模和方向分别为
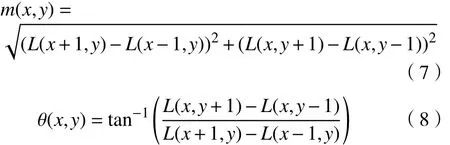
式中,L(x, y)是点(x, y)所在的尺度空间。
d. SIFT特征点匹配。
通过相似性对 SIFT 特征点进行配对。本文利用欧氏距离对SIFT的特征向量进行匹配,获得点对集S,完成特征点的粗匹配。
1.2 特征点对再筛选
获取两幅图像时的各种不确定因素会导致误匹配现象,进而直接影响配准结果,使得以该结果为依据进行的图像可信修补效果较差。所以在特征点粗匹配基础上要进一步筛选,以减小待修复图像和参考图像的配准误差。本文采用RANSAC(random sample consensus)算法进行特征点再筛选。
RANSAC匹配算法的基本思想是:为求出对应的目标函数,先随机选出M组数据,而目标函数就决定了每次抽取数据的个数;接下来用M组数据分别估算出目标函数的参数,再找出每组参数对应的内外点,求出每组参数的内点个数,内点个数越多,就表示该组模型目标函数中的参数越准确。本文采用投影变换模型,该模型需要的最小数据量为4 对匹配点,包含平移、旋转、缩放和拉伸形变,故该模型适用于所有不同情况拍摄得到的图像间的变换。
RANSAC算法的具体步骤为:
a. 在匹配点对集S中反复随机抽4对匹配点对,算出对应的变换模型;
b. 用点对集中所有匹配点对检验该变换模型,选出该变换模型的支撑点集,便是样本的内点对,再利用样本内点对算出欧式距离,欧式距离为

式中,n为满足该模型的内点个数;
c. 可根据内点个数与欧式距离选出两幅待拼接图像变换模型;
d. 重复进行步骤a, b,使之产生符合标准的最佳变换模型。
利用求出的最佳投影变换模型来表示待修复图像和参考图像像素之间的关系

式中,分别表示待修复图像和参考图像的齐次坐标,投影变换矩阵H本身是齐次,,两者相差一个非零常数因子。图4表示投影变换模型拼接过程,首先将参考图像I2通过最佳变换模型投影到待修复图像I1所在平面,得到图像,再找出待修复图像I1与图像重叠区域内的破损像素,并用图像中相应位置的像素来进行修复。
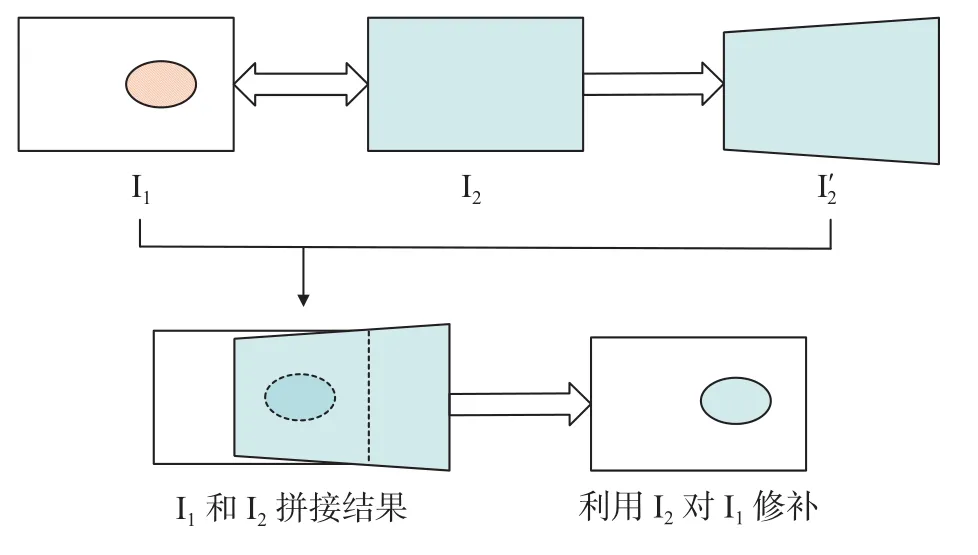
图4 投影矩阵模型拼接示意图Fig.4 Schematic of projection matrix model
当n = 4时,投影变换矩阵能求出唯一解;当n > 4时,投影变换矩阵的解就不再唯一。本文是运用RANSAC算法筛选出正确匹配特征点对,同时获得对应的投影矩阵H,再通过投影矩阵将参考图像投影在待修复图像上,完成配准和部分破损区域的修复工作。
1.3 图像自修复
因为本文研究的是修复大区域破损的图像,虽然经过前面在参考图像的配合下完成部分区域的可信修补,但仍可能存在一些破损区域,且只能依靠图像的自修复。这里选用针对大区域破损的Criminisi修复算法[6],该算法基于图像的纹理和结构来进行修复,在纹理复原方面较为优秀,但也存在修复算法的通病,即修复效果不太稳定。
Criminisi算法分为以下3个部分[7-8]:
a. 计算块的优先权。
p为选取在轮廓线上的目标像素,以p为中心的目标块,该块的优先权P(p)定义为
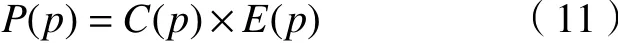
P(p)体现出待修复的块的置信度。式中:C(p)为置信度;E(p)为数据项。
式中,为点p等照度线大小与方向。
b. 找出最佳匹配块。
以p为中心的块的最佳匹配块Ψq为
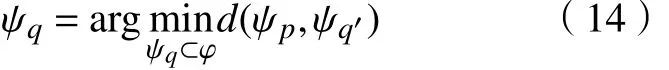
其中,

式中:;R(x)为像素x的红色分量;G(x)为绿色分量;B(x)为蓝色分量。
c. 修补该目标块并对置信度更新。
目标块修补完成后,便重新进行上两步,直至图像修复完成。
2 结果与分析
本文的图像修复在CPU为1.50 GHz,内存为4 GB的计算机上进行,该计算机为64 bit,Windows7的操作系统,在Matlab 2016a上完成编写。待修复图像在参考图像辅助下通过图像配准和投影完成图像可信修补,然后利用Criminisi算法完成图像的自修复过程。
图5是利用参考图像可信修复与自修复相结合所得到的修复结果。为了说明该系统的可行性,采样获得两幅相关图像,图5(a)为存在较大损坏区域的待修复图像,图5(b)为从另一角度拍摄得到的移位参考图像。可以看出两张图像存在重叠区域,需要通过图像配准达到可信修补。图5(c)为用SIFT算法在待修补图像和参考图像中获得的特征点的匹配情况,图5(d)是用RANSAC算法对图5(c)中的匹配点对进行进一步筛选得到精匹配点对,同时获得参考图像和待修补图像的投影模型。图5对应的投影矩阵为


图5 基于参考图像的可信图像修补结果Fig. 5 Trustable image inpainting results based on reference images
根据式(16)得到对参考图像的投影结果,如图5(e)所示。将该结果投影到待修复图像中,便得到图5(f),该图仍存在破损区域,需利用Criminisi算法进行最后的自修复,得到图5(g),至此修复完成。由该结果可以看出,通过参考图像修复的区域,不管结构还是纹理,基本符合实际情况。由于拍摄角度问题,不可避免地存在明暗色差,但基本不影响效果。在自修复方面,Criminisi算法是目前基于大区域修复较为优秀的算法之一,在图5的试验中,效果较理想且结构有所显现,但自修复本身就有不稳定的特性,无法对每个图像的修复效果有所保证。这两种修复算法相结合,可以最大限度地扬长避短。
图6为另一组图像的修复结果。可以看出,在待修复图像与参考图像间存在相对较大的位移和较复杂的变换关系,这里依靠约占50%的重叠区域,完成准确地待修复图像与参考图像的配准,保持了较稳定的修复效果。

图6 可信图像修补结果Fig.6 Trustable image inpainting results
图7是对该系统的实际应用,利用参考图7(c)对图7(a)中的遮挡物后方场景进行修补,利用图像配准得到的投影图像图7(d)进行修补,对剩余待修复部分进行自修复。可以看出,基于参考图像的可信修补结果理想且较为稳定,而需要自修复的破损区域较大时,自修复效果较不稳定。

图7 对图像中遮挡物的修补过程Fig.7 Trustable inpainting process for the image with marked occlusion object
图8 是基于多幅参考图像的修补过程,在这里对于一幅待修复图像获取了多幅相关的参考图像。图8(a)为待修复图像,可以看出损坏区域相对较大且分布较为均匀,不同复杂度的区域均存在破损,图8(b)、图8(c)和图8(d)是对应不同的待修复区域的3幅参考图像。可以看出,参考图像是其中一个单独的小事物,无需待修复图像的大环境就可以完成配准和图像的修补,这使得参考图像的获取更为便利。

图8 待修复图像和多幅参考图像Fig.8 Damaged images and multiple reference images
图9是图8中的3幅参考图像分别通过SIFT和RANSAC算法,与图8(a)进行配准,并在投影矩阵下产生的投影结果。再分别利用投影图像中相关像素对待修复图像进行修补,最终得到基于参考图像的可信修补结果,如图10所示。图11是待修复图像中剩余的破损区域利用Criminisi算法进行自修复的结果,至此该图像修补完成。

图9 参考图像的投影结果Fig.9 Projection results for reference images

图10 基于多幅参考图像的修补结果Fig.10 Inpainting results based on multiple reference images

图11 基于多幅参考图像的最终修补结果Fig.11 Final inpainting result based on multiple referenceimages
表1、表2分别为本文算法与Criminisi算法的峰值信噪比(peak signal to noise ratio,PSNR)、运行时间的比较结果。虽然参考图像与待修补图像之间存在亮度等差别,但在纹理、结构和真实性方面有着明显优势。从表1、表2可以看出,本文方法在PSNR和运行速度方面均有较大优势,且优势大小与基于参考图像的可信修补区域和自修复区域所占比例有着直接关系。
基于参考图像的修复效果比较稳定,SIFT粗匹配和RANSAC精匹配基本可以承受参考图像获取角度带来的很大程度的畸变,而Criminisi通过置信度和结构性函数来选出的最佳匹配块,在纹理和结构方面也能获得较为理想的效果,所以该系统对各种情况均有较好的稳定性。
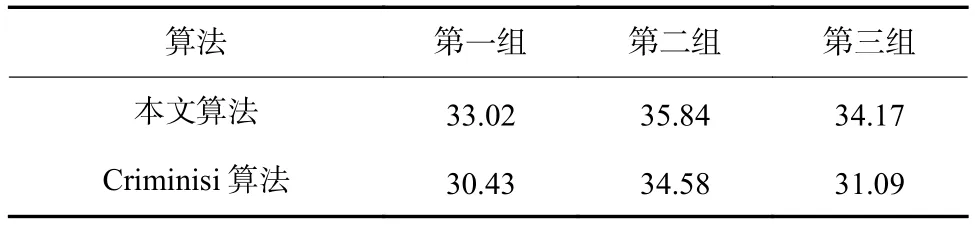
表1 两种算法的PSNR比较Tab.1 PSNR comparison between the two algorithms
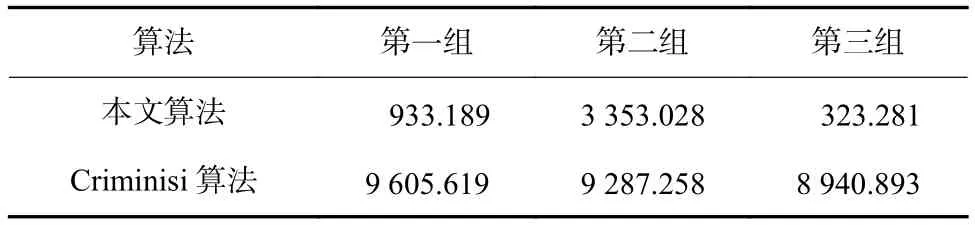
表2 两种算法的运行时间比较Tab.2 Execution time comparison between the two algorithms
3 结 论
对于图像修复方面,提出了一种基于参考图像的可信图像修补与图像自修复相结合的修复方法。该方法综合了图像拼接与图像修复各自的优点,即利用SIFT算法与RANSAC算法将参考图像中的相关信息投影在待修复图像上,之后再利用Criminisi算法进行最后的自修复。通过以上过程,使该方法在各种条件下皆有较高的适应性,且最大限度地提高了修复结果的可信度和稳定性。通过利用能够获得的多幅相关图像,从根本上解决了现有的自修复算法因缺乏已知信息而无法保证修复质量的问题。
参考文献:
[1]BERTALMIO M, SAPIRO G, CASELLES V, et al. Image inpainting[C]//Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM, 2000: 417-424.
[2]CHAN T F, SHEN J H. Non-texture inpainting by curvature-driven diffusions[J]. Journal of Visual Communication and Image Representation, 2001, 12(4):436-449.
[3]CHAN T F, SHEN J H. Mathematical models for local non-texture inpainting[J]. SIAM Journal on Applied Mathematics, 2002, 62(3): 1019-1043.
[4]SINGH M, KAUR H. Image inpainting in remotely sensed images by optimizing NLTV model by ant colony optimization[C]//Proceedings of the 2016 2nd International Conference on Next Generation Computing Technologies.Dehradun: IEEE, 2016: 687-693.
[5]DRORI I, COHEN-OR D, YESHURUN H. Fragmentbased image completion[C]//Proceedings of the 30th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM, 2003: 303-312.
[6]CRIMINISI A, PEREZ P, TOYAMA K. Object removal by exemplar-based inpainting[C]//Proceedings of 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Wisconsin: IEEE, 2003: 721-728.
[7]CHEN Z H, DAI C, JIANG L, et al. Structure-aware image inpainting using patch scale optimization[J]. Journal of Visual Communication and Image Representation, 2016,40: 312-323.
[8]LIU H X, SUN J X, SUN H B, et al. Image inpainting based on hidden Markov random field[C]//Proceedings of 2016 IEEE 13th International Conference on Signal Processing. Chengdu: IEEE, 2016: 697-701.
[9]SMEETS D, KEUSTERMANS J, VANDERMEULEN D,et al. Mesh-SIFT: local surface features for 3D face recognition under expression variations and partial data[J].Computer Vision and Image Understanding, 2013, 117(2):158-169.
[10]WANG J Z, MA Z Q, ZHANG B X, et al. A structurepreserved local matching approach for face recognition[J].Pattern Recognition Letters, 2011, 32(3): 494-504.
[11]HUANG Y, LI K, YANG M. An improved image inpainting algorithm based on image segmentation[J].Procedia Computer Science, 2017, 107: 796-801.
[12]HOSSEIN-NEJAD Z, NASRI M. An adaptive image registration method based on SIFT features and RANSAC transform[J]. Computers &Electrical Engineering, 2017,62: 524-537.
[13]KUO T Y, SU P C, KUAN Y P. SIFT-guided multiresolution video inpainting with innovative scheduling mechanism and irregular patch matching[J]. Information Sciences, 2016, 373: 95-109.
[14]刘春晓, 金剑秋, 彭群生. 利用大位移视图的自动可信图像修补[J]. 中国图象图形学报, 2013, 18(3): 351-357.
[15]梅杨杨, 谢海明, 韩露, 等. 基于Harris算子的图像拼接高精度检测技术[J]. 光学仪器, 2010, 32(1): 9-12.
[16]LOWE D G. Distinctive image features from scaleinvariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110.
[17]SMITH S M, BRADY J M. SUSAN-A new approach to low level image processing[J]. International Journal of Computer Vision, 1997, 23(1): 45-78.
[18]HARRIS C, STEPHENS M. A combined corner and edge detector[C]//Proceedings of the 4th Alvey Vision Conference. Manchester: Springer, 1988: 147-151.

