含需求响应特征矩阵函数的两阶段风险调度
潘 轩,周任军,刘镂志,李雪芹,殷旭锋
(湖南省清洁能源与智能电网协同创新中心(长沙理工大学),长沙 410114)
高比例风电接入系统带来了负荷低谷时弃风、负荷高峰时功率不足等一系列问题。目前解决该问题的方法主要有储能技术[1]、多能互补模式[2]、需求侧响应和“源网荷”的协同优化[3-4]等,均取得了较好的效果。其中,价格型需求响应PDR(pricebased demand response)在削峰填谷、消纳新能源、提高负荷率等方面取得了不错的效果。考虑电/热负荷需求响应和供需双侧热/电耦合可提高微网经济效益[5,光热电站和价格型需求响应参与风电消纳的调度可有效降低系统弃风率[6],将电热综合需求响应应用于园区微网综合能源系统,可减少弃风弃光,并提高系统经济性[7]。
然而,价格型需求响应作为有效负荷调节手段的同时也给系统引入了新的不确定因素[8],原因在于目前线性的价格型需求响应关系刻画不精确,且价格型需求响应存在一定波动性,会给系统增加新的风险。因此,有必要研究价格型需求响应参与后的风险规避问题。针对风险问题,当前研究主要在实时调度运行中采用不同的风险规避手段或模型,例如:文献[9]通过灵活应用中断负荷/电量收购和关键负荷电价等手段规避平衡市场所面临风险;文献[10]构建了考虑风光不确定性的虚拟电厂随机调度优化模型,通过灵活参与电力、碳交易和天然气市场来规避运行风险。以上模型多从规避风险的调节手段入手,较少从提高风险引入量的精确刻画来规避风险。
目前,价格型需求侧响应模型一般包含消费者心理学模型、电量电价弹性矩阵模型以及效用函数模型,其中电价弹性矩阵模型应用广泛,一般表达为电量电价弹性矩阵[11-12],元素取值多为线性关系,且不同时刻和不同价格变化量区间的响应系数取值相同。然而,用户的价格型需求响应关系往往表现出非线性和时间差异性[13]。非线性是指同一用户群体在同一时刻对不同区间的价格激励的响应是不同的,虽然在一定价格变化量区间范围内的响应系数可取描述为线性关系,但整个响应关系是不同线性关系的连接,因此,非线性描述更加适用于刻画响应的区间差异性。时间差异性是指同一用户群体在不同时刻具有不同的响应关系,这主要是因为不同时刻的用能需求具有差异性。通过对价格型需求响应关系的更精确刻画,可减少需求响应波动对系统的影响,从而一定程度上规避风险。
由于易受到生产生活、突发事件等多种客观因素的影响,价格型需求响应存波动性,这对响应实施策略带来了一定影响[14-15],且目前缺乏对需求响应波动量的详细刻画和论证。此外,当前较少同时考虑风电出力波动与价格型需求响应波动。
因此,本文应用自适应最优分割法[16-17]对非线性价格型需求响应关系进行拟合,考虑价格型需求响应波动,对电量电价弹性矩阵进行扩展,提出了需求响应特征矩阵函数。同时考虑风电波动,将需求响应特征矩阵函数计入采用条件风险价值CVaR(conditional value-at-risk)来度量系统不确定风险的优化模型,采用场景生成、削减技术模拟系统不确定性,以系统期望总收益最大为目标,并以虚拟电厂为背景,建立了含需求响应特征矩阵函数的两阶段风险调度模型。
1 电量电价需求响应特征矩阵函数
1.1 自适应最优分割法的特征函数描述
价格型需求响应是利用电价的变化作为刺激信号,刺激用户为了追求用电经济性而主动作出响应,进而到达削峰填谷增加风电消纳空间的目的。长久的价格刺激可以改变用户用电习惯,使用户的用电行为更加顺应某一特性。为了简化计算模型,许多学者通常采用线性的电量电价弹性矩阵来描述响应,然而实际响应并非是简单的线性关系。因此,有必要对价格型需求响应系数ε(Δq)做更精确的刻画,即

式中:ΔP、P分别为负荷变化量和响应前原始负荷;Δq、q分别为电价变化量和响应前原始电价;ε(Δq)为含变量Δq的响应系数函数。某时刻电价的变化对其他时刻负荷存在影响作用,为简化需求响应特征矩阵,本文将不同时刻电价变化带来的影响等效归结为自身。
为了对复杂关系进行更精细刻画,选取自适应最优分割法对复杂函数进行分段精确拟合[16]。自适应最优分割法能在包含多项式、正弦和指数等函数的库中根据某一规则来确定拟合方案,并将拟合所得到的函数表达式称之为“特征函数”。当拟合样本长度为n时,将i~j的样本分段称之为Gi,j={i,i+1,…,j},并用ftype,i,j表示i~j中样本数据使用type型函数,type={1,2,…,m},其中m是上述函数库中函数模型数量。最终可得到待拟合样本序列被分割为s段的表达式F(x)和对应参数[17],即

因此,选取不同样本,就有不同的函数表达形式和对应参数。抽取某时刻300组需求响应历史数据根据Δq进行排序,应用自适应最优分割法进行拟合,并用决定系数作为拟合判据。将本文拟合结果与传统线性描述做对比,得到如图1所示的结果。

图1 需求响应的不同刻画对比Fig.1 Comparison among different depictions of demand response
根据图1得特征函数表达式为
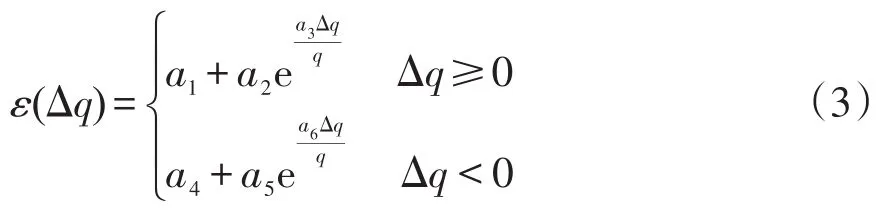
式中,a1、a2、a3、a4、a5和a6为拟合系数,其数值如表1所示。

表1 某时刻下拟合系数Tab.1 Fitting coefficient at one certain moment
分析图1与表1可知,所用拟合方法断点为0,计算应用最优分割法所得拟合曲线的决定系数为0.928,相比于传统的线性电量电价弹性系数方式提高了0.026。自适应最优分割法能拟合得到不同电价变化率区间的特征函数表达式,反映了需求响应关系的“区间”特性,特征函数的尾部反映了需求响应关系的“饱和”特性。
以上分析仅以某地区某时刻的需求响应说明本文拟合方法,同一地区不同时刻需求响应关系存在区别。同理求得基于自适应最优分割法的24时刻需求关系见表2。

表2 基于自适应最优分割法的24时刻需求关系Tab.2 Demand relationship in 24 h based on the adaptive optimal segmentation method
1.2 需求响应的波动性描述
实际响应时,负荷会受到生产生活、突发事件等多种客观因素的影响,因此用户的用电需求难以直接采用简单的确定性函数精确拟合。为了描述需求响应存在的不确定性,参照风电出力波动描述,引入随机波动变量ξq对其进行描述为

某时刻波动量计算公式为

应用Matlab中Q-Q图对历史所抽取的300组数据进行正态分布检验,如图2所示,并对其进行正态拟合,结果如图3所示。
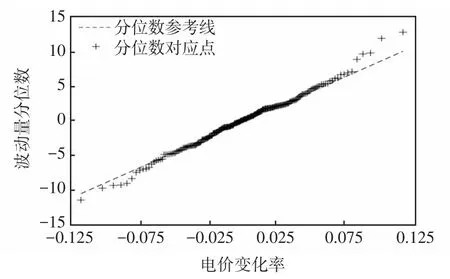
图2 需求波动量Q-Q示意Fig.2 Schematic of demand fluctuation Q-Q

图3 需求波动量正态分布拟合Fig.3 Normal distribution fitting of demand fluctuation


1.3 需求响应特征矩阵函数描述
将所得的全周期内t个时刻需求响应特征函数进行描述,得到需求响应特征矩阵函数为

计及随机波动后的需求关系为

式中:εt(Δq)为t时刻需求响应特征函数;Px和P分别为响应后和响应前的负荷;qt和Pt分别为响应前t时刻的电价和负荷;Δqt为t时刻电价变化量。
2 响应目标、不平衡惩罚机制与CVaR风险度量
2.1 响应目标
高比例风电参与调度中,通常会出现反调峰特性,即在负荷低谷时段,系统只能接受部分风电,造成大量弃风;在负荷高峰时段,系统的功率出现缺额。为了简化变量,在未考虑价格型需求响应前,将优化调度结果中的弃风和系统功率缺额作为响应目标。
2.2 不平衡惩罚机制
根据PJM电力市场不平衡惩罚交易机制,当实时市场中出现不平衡功率偏差时,这部分偏差量将在平衡市场中乘以惩罚系数进行交易[18],但目前惩罚系数多为固定值,这不能体现不同大小的功率偏差量对电力系统的不同影响。在平衡市场中,不同大小的功率偏差量造成的影响是不同的,如果针对不同的功率偏差量仍采用相同的不平衡惩罚系数显得不太合理,因此,依据不平衡功率偏差来确定惩罚系数。不平衡惩罚系数表示为

式(9)体现不同功率偏差量带来的不同影响,即功率偏差量越大对电力系统安全稳定性影响越大,其惩罚系数也应该越大,从而更能刺激电能交易参与方采取措施减少平衡市场功率偏差量。
2.3 CVaR风险度量
目前风险度量的常用方法有加权期望法、VaR和CVaR等,本文采用CVaR度量虚拟电厂调度的预期风险。CVaR考虑了VaR中的尾部风险[19],揭示了所实施策略超过某个给定VaR值的平均损失,表示为


3 含需求响应特征矩阵函数的两阶段风险调度模型
3.1 含需求响应特征矩阵函数的风险规避目标函数
本文选取常规火力发电机组、风电商和柔性负荷所构成的虚拟电厂进行研究,并以考虑风险规避的虚拟电厂调度收益最大来实施策略,其目标函数为

式中:EDR为日前方案收益;EP为实时方案预期收益;γ为风险规避因子,γ越小表示调度模型越接受风险,γ越大表示调度模型越想规避风险。
3.1.1 日前调度
日前调度是在前一日预测未来一日T时段的风电出力和负荷数据,根据一定的经济准则来安排第2天各时段各电源的发电计划。以虚拟电厂调度收益最大为目标函数,有

其中,R1,t为考虑价格型需求响应后t时刻售电电收益,表示为

式中:Px,t为t时刻需求响应后的期望负荷功率;qx,t为日前响应后t时刻的计划电价;Δt为仿真步长,取值1 h。
R2,t为t时刻火电机组的运行成本,表示为

式中:N为火力发电机组台数;Pi,t为第i个火力发电机组在t时段的出力;ai、bi、ci为火力发电机组的运行参数;zi,t为第i个火力发电机组在t时段的启停状态,zi,t=0代表停机,zi,t=1代表开机;Si为第i个火力发电机组的启停费用。
R3,t为t时刻弃风惩罚成本,表示为

式中:λqw为弃风惩罚系数,取值800元/(MW·h);Pqw,t为t时刻弃风量。
需求响应约束取式(1)。
功率平衡约束为

式中:Pi,t为第i台火力发电机组t时刻出力;Pw,t为t时刻风电调度出力;Px,t为t时刻需求响应后的负荷。
响应目标约束为
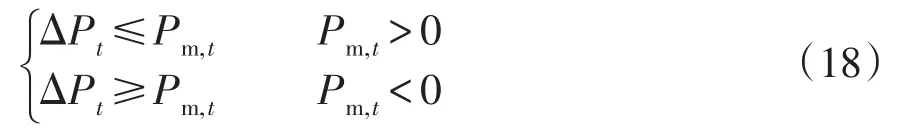
式中,ΔPt和Pm,t分别为t时刻需求响应量和响应目标。

用电满意度约束为
当层间位移角到达7%rad,即梁加载中心点位移76.38 mm,接近位移极值时,角钢被较为明显拉起。当层间位移角到达8%rad(89.11 mm)时,随着节点转动角度增大,转动过程中梁翼缘受角钢挤压变形,与角钢翼缘产生间隙。而梁腹板也出现较为明显的受压变形导致的曲鼓。

式中,ms为用户用电方式的满意度[5],用响应前后用户在各时段用电量的改变情况刻画为


式(20)中,mj为用电单价满意度,用响应前后用户电费的变化情况刻画为
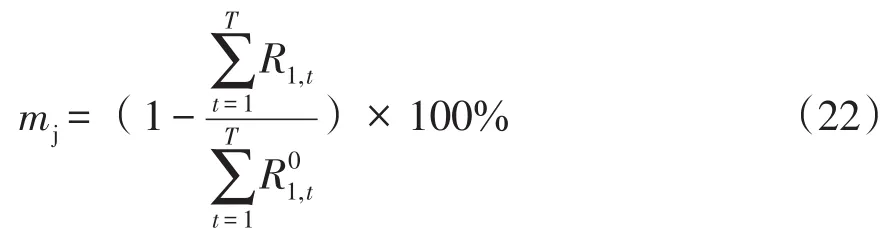
机组爬坡约束为

式中,Pi,N为第i台火力发电机组额定功率。
3.1.2 实时调度策略
实时调度是考虑风电出力波动和需求响应波动带来的偏差,在日前调度基础上对系统进行优化调度。以虚拟电厂调度收益最大为目标,即

因此,实施策略损失函数损失函数为
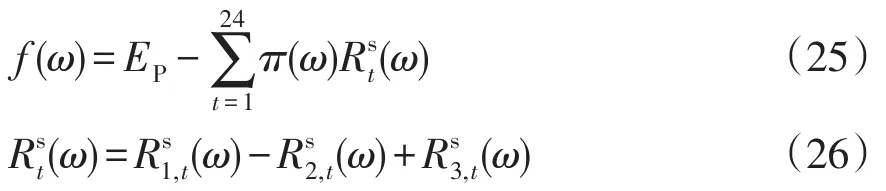
售电收益变化为

发电成本变化为
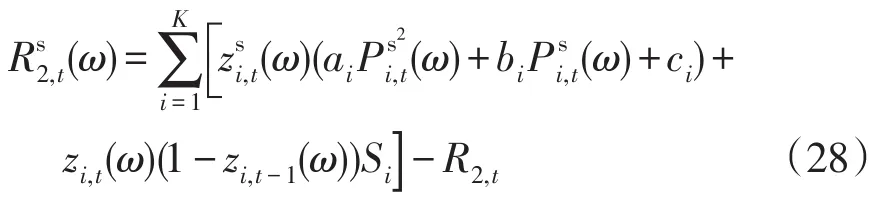
由于系统存在风电和需求响应波动,使得实时调度与日前调度运行状态存在一定偏差,这部分偏差量将在平衡市场中以一定惩罚进行交易。则平衡市场收益为

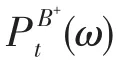
功率平衡约束为

本文实时调度策略中约束还包括式(17)~式(22),此处不再赘述。
3.2 风电与需求响应波动的多场景生成和求解方法
根据需求响应波动和风电波动的分布函数,采用Monte-Carlo法生成多个需求响应和风电预测偏差场景[20],将需求响应场景与期望负荷功率相加得到实际负荷场景,同理可得到实际风电出力场景。为减少计算负担并保持一定的可信性,使用概率距离的思想对相似场景进行缩减,文章采用快速前向选择法进行场景缩减[21]。
考虑多波动的CVaR风险度量模型的求解研究已比较常见,本文采用文献[19]的求解方法求解。
4 算例分析
4.1 算例参数


表3 常规火电发电机组参数Tab.3 Parameters of conventional fire power generator set

表4 不平衡系数取值Tab.4 Values of unbalance coefficients

图4 电价曲线Fig.4 Curves of electricity price

图5 预测风电、原始负荷与响应目标曲线Fig.5 Curves of forecasted wind power,raw load,and response target
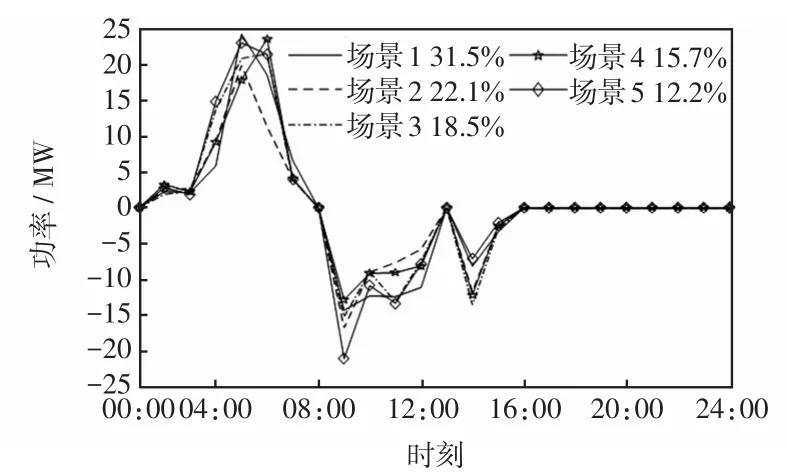
图6 需求响应场景Fig.6 Scenario of demand response

图7 风电场景Fig.7 Scenario of wind power
4.2 算例方案设置
为便于分析讨论,目标函数置信度 β=0.9,γ=1,msmin为90%,mjmin为95%,共设置2个方案。
方案1:线性响应矩阵关系下同时考虑风电出力和需求响应波动。
方案2:需求响应特征矩阵函数下同时考虑风电出力和需求响应波动。
4.3 结果分析
4.3.1 日前调度分析
不同方案下的电价调整计划如图8所示。由图8可知,针对同一响应目标,方案1和方案2所实施的日前调整价格计划不同,其根据原因是方案1和方案2所采用的需求响应关系刻画不同。此外,当响应目标绝对值较小时,两中方案的电价调整计划相近;当响应目标绝对值较大时,2种方案的电价调整计划具有明显差距。不同方案下日前收益分析如表5所示。

图8 不同方案下的电价调整计划Fig.8 Plan of electricity price adjustment in different cases

表5 不同方案下日前收益分析Tab.5 Analysis of day-ahead earnings in different cases 元
结合图8和表5可知,方案2的日前收益高于方案1,这是由于方案2相比于方案1中需求响应关系,未考虑需求响应关系的“尾部饱和特性”,认为可通过较小电价调整获得较大的需求响应量。
4.3.2 实时调度
由表6可知,方案1的平衡市场收益高于方案2,使得方案1的实时期望收益高于方案2,其原因是方案1的日前需求响应关系刻画更精确,所实施的日前电价调整计划更准确,降低了实时市场中的成本。表5中,由于需求响应波动符合正态分布,因此售电收益变化较小,基本不会影响收益;由于日前方案中的传统机组爬坡、功率上下限等已经接近约束极限,实时调度中已不再调整。

表6 不同方案下实时期望收益分析Tab.6 Analysis of real-time expected return in different cases 元
4.3.3 风险偏好分析
为了比较不同风险偏好程度对调度的影响,对方案1和方案2设置不同的风险系数进行对比分析,结果如表7和表8所示。为了直观比较2种方案的收益情况,将日前收益和实施期望收益之和为期望总收益。
由表7和表8可知,方案1和方案2的期望总收益均随着风险系数增加而减小,这是因为风险主要是系统波动量引起偏差量造成的。当风电所造成的波动无法改变时,随着风险系数增加调度只能通过减少价格型需求响应的调节程度来减少波动,从而规避风险。此外,期望总收益和风险损失体现了“低收益-低风险”的风险规律,调度可根据自身风险偏和风险规律来设置风险系数。

表7 方案1下不同风险系数分析Tab.7 Analysis of different risk coefficients in Case 1 元

表8 方案2下不同风险系数分析Tab.8 Analysis of different risk coefficients in Case 2 元
不同风险系数下的方案对比分析结果如图9所示。由图9可见,方案1与2的总收益之差为正,CVaR之差为负,说明本文的价格型需求矩阵关系相比于传统线性价格型需求响应关系,可一定程度上增加期望收益和规避风险,且当风险系数较小时,效果更为明显。

图9 不同风险系数下的方案对比分析Fig.9 Comparative analysis of cases at different risk coefficients
5 结语
采用自适应最优分割法获得了分段或非线性的需求响应特征矩阵函数,并对价格型需求响应波动做了量化描述,相比于传统线性价格型需求响应矩阵,本文所刻画的需求响应特征矩阵函数更精确,考虑波动更符合客观情况。将需求响应特征矩阵函数计入风险规避的优化模型,并通过仿真对比分析了不同需求关系刻画下的总收益和CVaR,结果表明,本文模型一定程度上能规避风险和提升期望总收益,验证了本文所刻画关系和模型的有效性,可为风险规避问题提供借鉴思路,为不同风险偏好程度的调度提供参考。

