揭示隐含条件的几个藏身地
浙江省嘉兴市嘉善第二高级中学 (314100) 孙洪梅
在某些数学命题的题设中,已知条件或欲求结论中还可能隐含某些信息,或在解题过程中所得到的结论也隐蔽着大小关系、取值范围等,我们称之为“隐含条件”.在解题中,如果我们不能及时披露题目中隐含条件,一般会造成解题错误或者解题过程繁琐,亦或者认为题目缺少条件而束手无策.针对此类问题,本文通过举例分析,揭示隐含条件的一般藏地及如何寻找隐含条件,供读者朋友参考.
一、隐含在数学概念中
许多概念都是定义在相关条件上的,遇到这些概念就应该联想到建立此概念所必须满足的条件,关注这些条件并合理运用非常重要.
例1 设A={x|x2-8x+15=0},B={x|ax-1=0},若A∪B=A,求实数a的值.

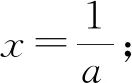
例2 设钝角三角形的三边长分别为k、k+1、k+2,求实数k的取值范围.
解析:设最大边k+2所对的角为θ,则θ必为钝角,故有cosθ<0,由余弦定理得,cosθ=
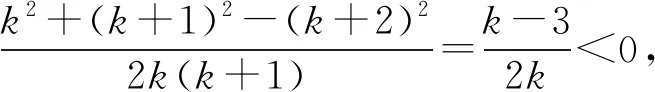
评注:这里容易忽视“三角形任意两边之和大于第三边”这一构成三角形的重要条件,造成错解.
二、隐含在数学公式中
一些数学公式必须在一定条件下才能得到,在使用这个公式时要考虑使用条件,不可盲目套用.
例3 已知数列{an}满足a1+2a2+3a3+…+nan=2n2+1,求通项公式an
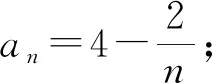

评注:对于Sn-1来说,蕴含着条件n≥2,所以关系式an=Sn-Sn-1在n≥2时对任何数列都适用,但当n=1时不适用,即不要忘记对n=1进行验证.
例4 已知a>0,求函数y=(sinx+a)(cosx+a)的最大值和最小值.


三、隐含在已知条件中
在一些题目中,条件比较隐晦,不能一眼看透,需要加强分析、特值探求,或有意识的反思等方法找到条件.
例5 已知3sin2α+2sin2β=2sisα,求sin2α+sin2β的取值范围.



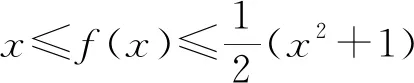
评注:在本解法中,利用特殊值进行验证获得了f(1)=1这一隐含信息,得到了关于系数a、b、c的一个关系式,这是破题的关键所在.
四、隐含在待求结论中
如果题目的条件简单,而欲求结论相对复杂,通过化简、变形这个结论就可以挖出当中所含的条件或提示.


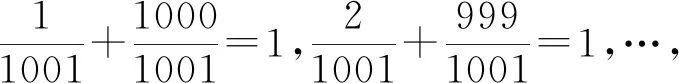
评注:有些数学题中隐含着等式关系,它提示了该数学问题的本质,挖掘出这些隐含的等式关系,就是我们解答此问题的切入点.
例8 △ABC的三边a,b,c和面积S满足关系S=c2-(a-b)2,且a+b=2,求面积S的最大值.
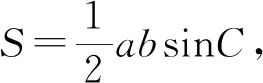
评注:题中要求的是三角形面积的最大值,何时取最大是问题的关键,所以首先根据题意从题设中挖掘出角C的取值情况非常重要.
五、隐含在图象、图形中
有一些几何图形、几何体粗看上去不易理解,但通过连辅助线、拆分图形,把已知条件进行整合,就能找出隐含的关系或结论.
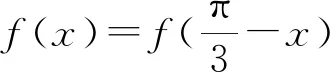
A.0 B.3 C.-3 D.3或-3
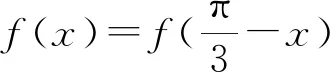
评注:由于题设中只有一个条件,故需研究三角函数图象的特征,再充分运用这个条件,这样就撇开了参数ω、φ,进行整体分析,整体求解.
例10 如图1,已知ABCD-A1B1C1D1是棱长为a的正方体,E、F分别为AA1与CC1的中点,求四棱锥A1-EBFD1的体积.

图1
解析:容易求出EB=BF=FD1=D1E=

评注:本题中直接求体积比较困难,但通过分割、换底变高转化,将难以计算的底与高转化为已知的底与高的三棱锥,这就是挖出了几何图形中所隐含条件,从而使问题轻松化解.
六、隐含在解题过程中
在解题过程中可能得到许多的中间结论,若能及时发现,及时利用,可简化解题过程,提高解题的正确率.



评注:在对条件的化简变形中,及时的抓住2sinαcosα<0这个隐含条件,确定了sinα- cosα的取值,从而避免了增解的发生.
例12 设A和B为抛物线y2=4px(p>0)上原点以外的两个动点,已知OA⊥OB,OM⊥AB,求点M的轨迹方程,并说明它表示什么曲线.
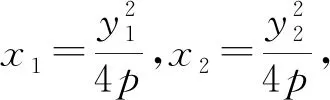
评注:在解题过程中,得到了直线AB过定点Q(4p,0),再由OM⊥MQ,根据圆的定义直接得出点M的轨迹方程,不放过这个解题途中获得隐含条件是破题关键.

