初中高中两相依，它山之石可攻玉*——平几知识在解几中的应用

福建省厦门大学附属实验中学 (363123) 王亚坤 林秋林

一、问题提出

解析几何的本质是用代数方法研究图形的几何性质，体现了数形结合的重要数学思想，在高考中有着重要的地位，是高考命题的热点之一．一般来说，解析几何综合问题主要以圆锥曲线为载体，综合各个模块知识，全面考查学生分析问题、解决问题的能力，对逻辑思维能力与运算能力要求较高，有一定的难度.学生在解答解析几何综合问题时，习惯于先联立直线与圆锥曲线的方程，再通过代数方法进行推理，往往导致运算量太大而不得不中途放弃．事实上，“解析几何也是几何”，其本身也隐含着平面几何的思想方法.在解答某些解析几何问题时，如果注重“初高中结合”，充分利用图形的直观性和平面几何知识，灵活处理，不仅能避开繁琐的代数运算，还能揭示问题的几何本质.同时，借助几何直观，利用平面几何的思想方法解决问题，有助于提高学生的实践能力，提升创新意识，发展直观想象、逻辑推理等数学学科核心素养.

二、应用举例

1.应用“勾股定理”

例1 (2020年高考全国Ⅰ卷)已知圆M:x2+y2-2x-2y-2=0，直线l:2x+y+2=0，P为l上的动点，过点P作圆M的切线PA,PB，且切点为A,B，当|PM|·|AB|最小时，直线AB的方程为( ).

A.2x-y-1=0 B.2x+y-1=0

C.2x-y+1=0 D.2x+y+1=0

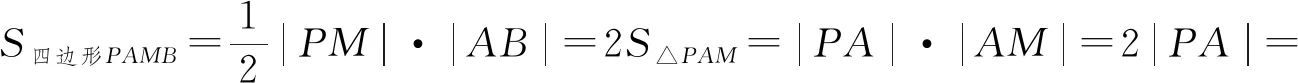
2.应用“三角形中位线”

图1

3.应用“相似三角形”

例3 (2019年高考全国Ⅰ卷)已知椭圆C的焦点为F1(-1,0),F2(1,0)，过F2的直线与C交于A,B两点．若|AF2|=2|F2B|，|AB|=|BF1|，则C的方程为( )．

图2

4.应用“直角三角形斜边上的中线等于斜边的一半”

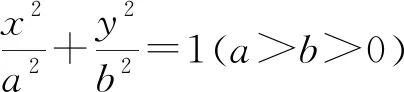
图3

5.应用“等积法”

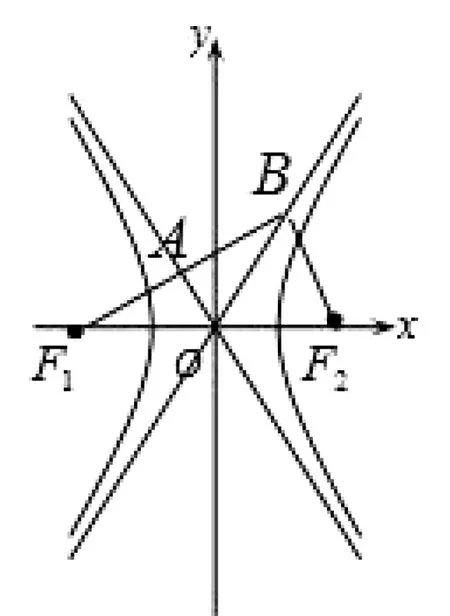
图4

6.应用“圆的性质”

例6 (2014年高考课标Ⅱ卷)设点M(x0,1)，若在圆O:x2+y2=1上存在点N，使得∠OMN=45°，则x0的取值范围是( ).

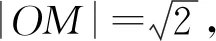
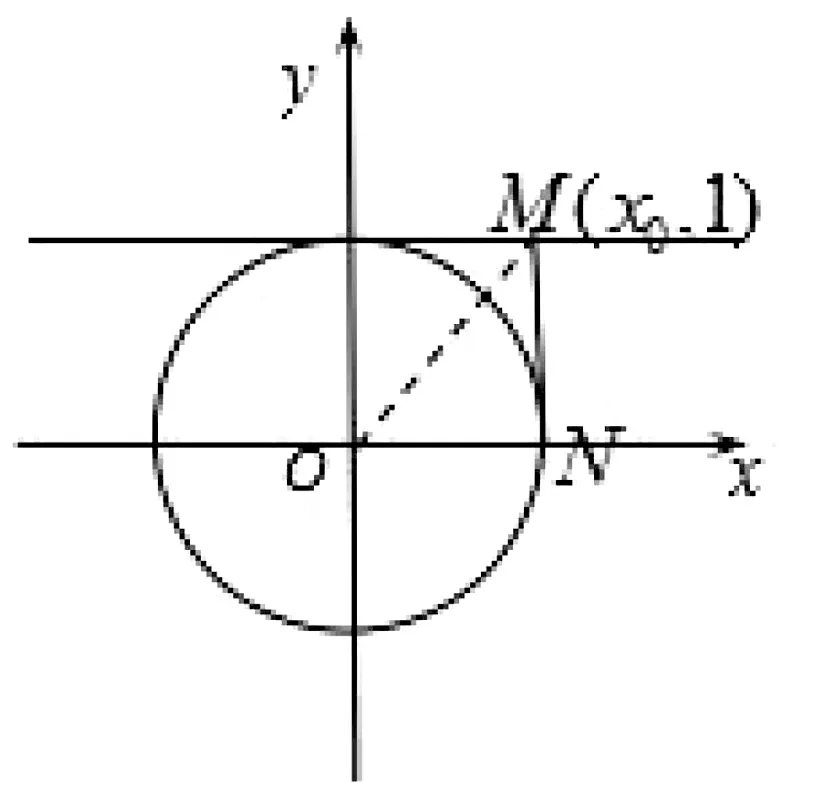
图5

7.应用“平行线和等腰三角形的性质”

(1)当l与x轴垂直时，求直线AM的方程；

(2)设O为坐标原点，证明：∠OMA=∠OMB．

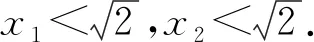
图6

三、结语

《普通高中数学课程标准(2017)》指出：“教师要帮助学生完成从初中到高中数学学习的过渡，包括知识与技能、方法与习惯、能力与态度等方面”[1].平面几何“讨论点，直线，直线的平行和垂直，三角形，圆等.这是平面图形中最基本、最简单者，然而也是培养学生的几何直观能力和进一步用坐标法讨论曲线的基础.”[2]圆锥曲线的学习中，一般是给出它们的几何定义后，便用数形结合的代数方法——“坐标法”来讨论它们.基于此，在解答解析几何问题时，要自始至终贯穿数形结合的思想，在图形的研究过程中，注意代数方法的使用；在代数方法的使用过程中，加强与图形的联系.借助平面几何的知识解决解析几何问题，有助于把握问题的几何本质，有效控制运算量.更重要的是，在解决解析几何问题时，回归“圆锥曲线的定义”，灵活利用图形的直观性和平面几何中的相关结论，其实质就是重新审视数学概念并用概念解决问题，这是一种朴素而又重要的策略和思想，有助于使学生体会数学知识之间的有机联系，感受数学的整体性，发展直观想象、逻辑推理等数学学科核心素养，提升创新意识.