数学课堂教学中培养学生理性精神的几点做法*

江苏省江阴市第一初级中学 (214400) 钟珍玖

数学课堂教学应该在类比、归纳、猜想中培养严密逻辑思维能力，形成科学精神，在探究、发现、问题解决中培养学生独立思考的习惯，在提倡问题开放、思维发散和多样性中培养自由思想，在大胆质疑中追求真理，让核心素养在课堂教学中的落地生根.

1 关于理性精神

在哲学中，理性是指人类能够运用理智的能力.相对于感性的概念，它通常指人类在审慎思考后，以推理方式，推导出结论的这种思考方式.从数学发展史来看，数学被看成一种理性的解释系统，为数学创造了不依赖现实世界的思维创造系统，所以M.克莱因认为“在最广泛的意义上说，数学是一种精神，一种理性精神.正是这种精神，使得人类的思维得以运用到最为完善的程度，亦正是这种精神，试图决定性地影响人类的物质、道德和社会生活，试图回答有关人类自身存在提出的问题，努力去理解和控制自然，尽力去探求和确立已经获得知识的最深刻的和最完美的内涵.”从数学本身的特点来看，数学的严谨性和逻辑严密性也是培养学理性思考的绝好素材.从数学教育课堂形态来看，数学的定理发现和证明、公式规则的推导，需要学生有探究精神、独立思考的习惯、追求真理的科学态度和质疑的精神.

2 数学课堂教学中培养理性精神的几点做法

数学课堂教学不仅仅是解题教学，学生学习数学的目标也不是只是学会解题，数学教学要根据数学的学科特点，让学科教学不仅是传授知识，而是要以素养立意，让学生的核心素养在课堂教学中落地生根，发挥数学教学的育人价值.

2.1 在类比、归纳、猜想中，培养学生理性思考的意识

从初中生的数学学习实际情况来看，学生的数学学习特别是几何内容的学习，还是以图形直观为主，缺乏对问题的严密分析和论证.从学生的学习特点来看，初中生的思维正从直观想象向抽象概括过渡，需要深入的思考和严密的推理提高抽象水平和抽象能力.所以初中生的数学教学要引导学生从“直观猜想”走向“逻辑推理”，形成言之有物、言之有据的习惯，要有尊重事实，实事求是的态度.

案例1 苏科版《义务教育教科书数学》七年级(上)，6.3余角、补角、对顶角教学片段.

师：2条直线相交成的对顶角有几对？3条直线相交于同一点所成的对顶角有几对？4条直线相交于同一点所成的对顶角有几对？请归纳n条直线相交于同一点所成的对顶角有几对？

生1：分别为2对，6对，8对，…，2n对.

师：为什么？

生1：2条直线相交有2对对顶角，3条直线相交于同一点，由于每两条直线相交有2对对顶角，3条直线就有6对对顶角，这样4条直线交于同一个点就有8对对顶角.

经过在教师巡视发现，班级绝大多数学生的答案都和生1一致，学生展开小组讨论.

生2：4条直线交于同一点，对顶角有12对，可以画图去计数.

师：直线较多，数对顶角的对数容易重复和遗漏，有没有其它想法？

生3：根据生1的想法，4条直线两两组合是6种两条直线相交的情形，而不是4种，所以对顶角有12对，根据前面的规律，n条直线相交于同一点所成的对顶角有n(n-1)对.

师：还可以这样考虑，3条直线交于同一点有6对对顶角，增加1条直线和前述3条直线各构成两对对顶角，所以4条直线交于同一点共有12对对顶角.

学生理性精神的培养不仅是在以实验为主的自然科学中渗透，数学学科的学习也是培养理性精神和科学精神的绝佳素材.数学学习中充满着归纳和猜想，数学概念的形成，数学公式和法则的得出，定理的发现和证明，都需要通过归纳和猜想来实现，归纳和猜想可以让我们发现新的结论，另一方面数学是一门抽象性和严谨性结合的学科，有时直观感知或者是从特殊情形出发的归纳不一定正确，所以教师在教学中要强调计算的准确，逻辑的严密，推理的有据，教给学生科学的思维方法，如观察、概括、抽象、推理、综合、分析等方法.在日常的课堂教学中引导学生发现的同时，养成言之有物、言之有据的习惯，注重思维发散性，更应让思维更严密，培养科学态度和理性精神.

2.2 在探究、发现、问题解决中，养成独立思考的习惯

学生的数学学习就是进行数学活动的过程，数学活动虽然也可以动手操作，但更多的是思维活动，需要学生学会思考.从长期的课堂教学实践来看，独立思考是学生学好数学的前提和保障，学生在课堂学习中要独立解决老师提出的问题，课后巩固练习中更需要培养独立作业的习惯和意识.对此，《义务教育数学课程标准》(2011版)就明确指出：在参与观察、实验、猜想、证明、综合实践等数学活动中，发展合情推理和演绎推理能力，清晰第表达自己的想法，学会独立思考，体会数学基本思想和思维方式，修订版的数学课程标准更加凸显了独立思考对数学学习的重要性.

案例2 苏科版九年级《圆的内接四边形》教学片段.

生1：类比圆周角定理的证明，如图1从特殊情况入手，当BD是⊙O的直径时，结论是成立的.∵BD是⊙O的直径，∴∠A=∠C=90°，∴∠A+∠C=180°，同理∠B+∠D=180°.

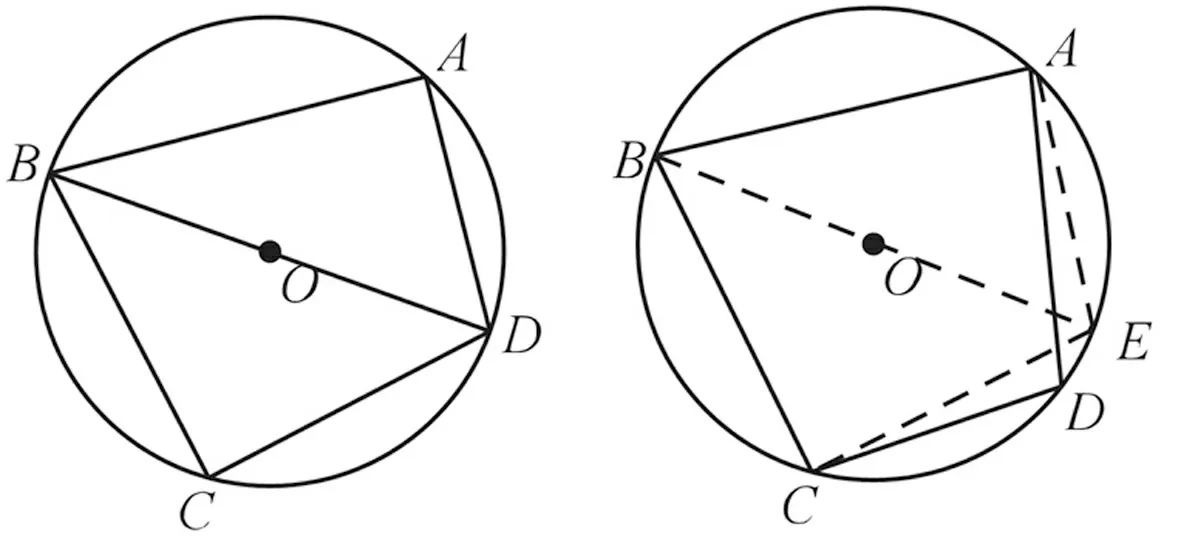
图1 图2

当点O不在四边形ABCD的对角线上时，如图2，证明如下：

连接BO并延长，交⊙O于点E，由图1证明可得∠BAE+∠BCE=180°.∵∠BAE=∠BAD+∠DAE，∠BCE=∠BCD-∠DCE，∴∠BAD+∠DAE+∠BCD-∠DCE=180°，∵∠DAE=∠DCE，∴∠BAD+∠BCD=180°.

(正当笔者准备继续讲解后面的内容时，还有学生举手发言)

生2：还有其他的方法证明这个定理，如图3，证明如下：

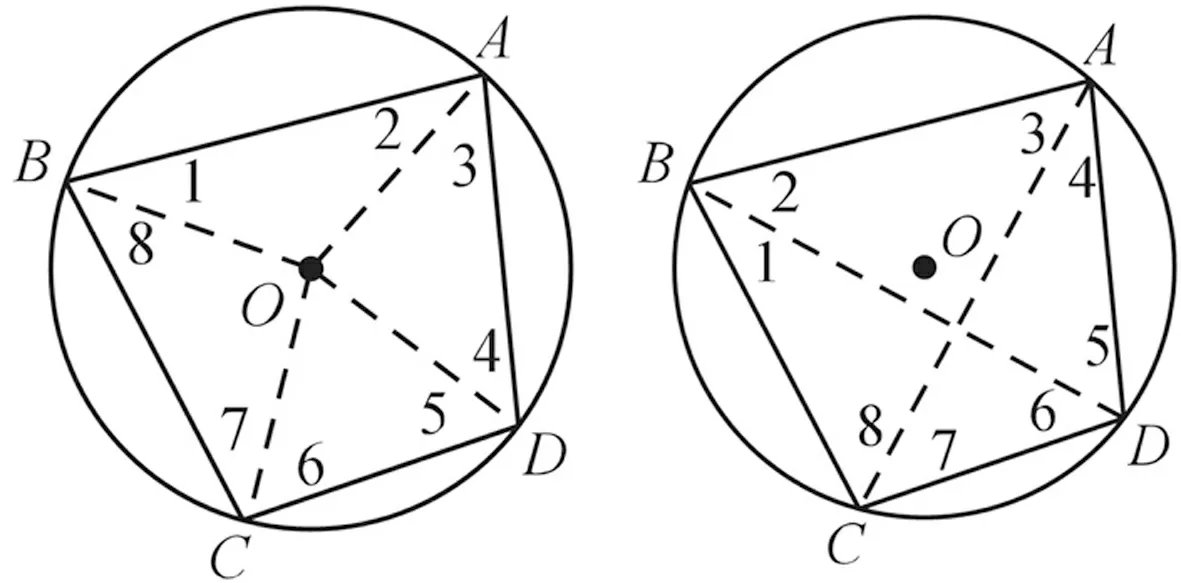
图3 图4

连接OA、OB、OC、OD，∵OA=OB=OC=OD，∴∠1=∠2，∠3=∠4，∠5=∠6，∠7=∠8，∴∠2+∠3+∠6+∠7=∠1+∠4+∠5+∠8=180°，∴∠BAD+∠BCD=∠ABC+∠ADC=180°.

生3：∵∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8=360°，∠1=∠4，∠2=∠7，∠3=∠6，∠4=∠8，∴2∠4+2∠3+2∠7+2∠8=360°，∴∠4+∠3+∠7+∠8=180°，∴∠BAD+∠BCD=∠ABC+∠ADC=180°.

实践证明，学生独立思考的意识和习惯与教师的教学行为是密切相关的，教师的教学不能为了节约时间而“满堂灌”，用教师的讲解代替学生的思考.对于这个定理的证明的多样性证明方法，是教师在课堂上给予学生足够独立思考的时间空间而形成的.教师的课堂教学应该不放过每一个有思考价值的问题，包括定理的发现、公式的推导、例题的讲解、作业的纠错，首先要让学生自己独立思考，教师不要包办，为了节省时间而采用满堂灌的输入式教学，这样的教学离学科育人相差甚远.

2.3 在思辨、争鸣、质疑中，形成探求真理的态度

数学的真理性是数学的特征，在现代数学中，由于高度的抽象化、形式化和公理化，人们常常认为逻辑相容性(无矛盾性)是检验数学真理的惟一标准.实际上，只有在数学的实践中，人们认识才能同客观的数学规律接近，从而确定数学真理.学生对真理的探究需要教师的不断引导，提高课堂教学的立意和品味，把数学育人的理念落实到课堂教学中.

案例4 给出下列4个命题：

①两边及其中一边上的中线对应相等的两个三角形全等；②两边及其中一边上的高对应相等的两个三角形全等；③两边及一角对应相等的两个三角形全等；④有两角及其中一角的角平分线对应相等的两个三角形全等．其中正确的的个数有( ).

A．1个 B．2个 C．3个 D．4个

解析：命题①和④只要证明2次三角形全等即可，命题②和③是假命题，其中命题③举反例来推证学生比较熟悉，对于命题②笔者也简单画了草图认为是真命题，课后有个学生用如图5所示的网格画图举反例，说明此命题时假命题.

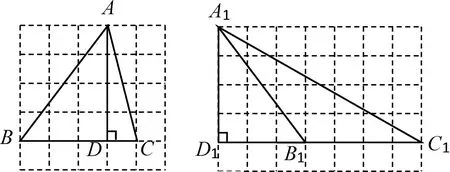
图5

数学课堂教学是培养学生追求真理的极佳场所，数学问题的解决、数学思维的优化、数学本质的探求，都需要有挑战困难的信心和不畏权威的勇气.教师的教学要引导学生以理性和包容的态度对待所学知识以及思考问题、解决问题中的不同观念，做到不唯书、不唯师、只唯实，有追求真理的勇气和态度.因此，教师的教学过程应该是态度民主、形式开放、鼓励创造和创新.